Білюк А.І., Білюк
А.А., Чехівська Ю.С., Вітюк Г.В.
СТРУКТУРНІ
ЗМІНИ КОНСТРУКЦІЙНИХ МАТЕРІАЛІВ ПІСЛЯ ТЕРМОЦИКЛЮВАННЯ
Формування та стабiлiзацiя
в алюмінії, міді та їх сплавах дислокацiйної субструктури перш за все переслiдує мету пiдвищення їх
фiзико-механiчних властивостей[1,2,5]. Використання цих матерiалiв в
машинобудуваннi потребує забезпечення стабiльних пiдвищених властивостей в
широкому температурному iнтервалi[3,5].
В даній роботі приведені
результати досліджень модулів пружності і мікротвердості дисперсійно-твердіючих
сплавів Al-4%Cu, Al-4%Cu-1%Zn , БрБ2 після термоциклювання (ТЦО). ТЦО
проводилось в інтервалі температур (768-793Û20)К із швидкістю нагрівання і охолодження 50 К×с-1.
Дослiдження модуля зсуву
алюмiнiєвих сплавiв проводились динамiчним методом пiсля ТЦО на низькочастотному (~1Гц) приладі типу
оберненого крутильного маятника[3,4]. Мікротвердість Нm вимірювали на приладі ПМТ-3. Розмір відбитка брався
середнім з 15-20 уколів призми.
Дослідження показали, що
модуль зсуву зазнає суттєвих змін при температурах формування і стабілізації
зміцнюючої субструктури (рис.1). Максимальне значення модуля зсуву досягається
після 30-40 ТЦО. Наступне збільшення кількості термоциклів веде до зменшення цієї
величини. Інтенсивність зміни модуля зсуву визначається ступінню нерівноваженості
структури досліджуваних матеріалів. Крім цього, така зміна величини G(f2)
свідчить
про підвищення жароміцності субструктурно-зміцнених
матеріалів [6].
Досліди по вимірюванні
мікротвердості показали, що залежність діаметра відбитка d від навантаження P
має параболічний характер: 
де a i nm
- постійні. В логарифмічних координатах можна одержати лінійну залежність між lnP i lnd, причому константа ln a грає роль екстрапольованої межі
текучості sо, а константа nm
- роль коефіцієнта зміцнення (показник Майєра [7]).
Виявлено загальні
закономірності поведінки величин Hm i nm після ТЦО для сплавів на основі алюмінію
і міді (рис. 2-4).
Аналіз результатів досліджень дозволяє скоректувати число ТЦО так, щоб одержати підвищення механічних характеристик при збереженні на достатньо високому рівні демпфуючих властивостей, підвищити однорідність структури і зменшити короблення деталей.
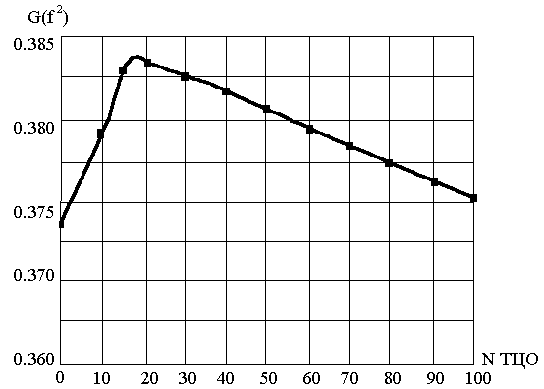
Рис.1 Залежність модулю зсуву G (f2) від кількості ТЦО.
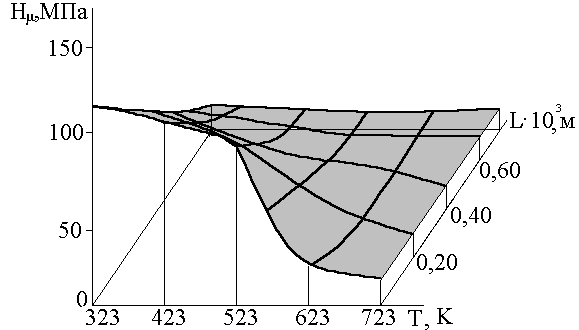
Рис.2 . Залежність мікротвердості алюмінієвих сплавів Нm від температури Т і віддалі від краю зразка
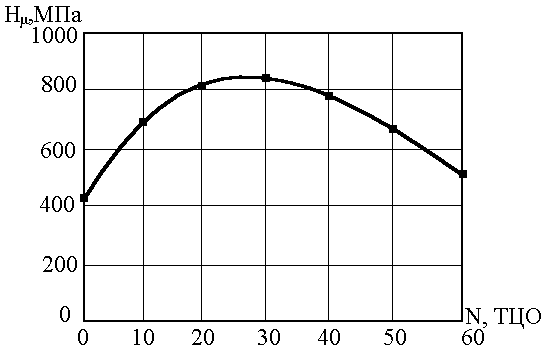
Рис. 3. Залежність мікротвердості
мідних сплавів Hm від кількості ТЦО
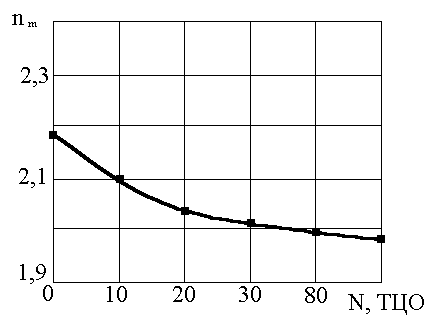
Рис.4 . Залежність показника Майєра мідних сплавів від кількості ТЦО.
ЛІТЕРАТУРА
1.
Білюк А.І. Вплив
термоциклювання під навантаженням на структурні зміни дисперсійно-твердіючих
алюмінієвих сплавів // Металлофизика и новейшие технологии. – 1997. – Т.19. –
№6. – С. 78-80.
2. Зузяк П.М. Поглощение упругой энергии в метастабильных
металлических системах // Автореферат диссертации доктора физико-математических
наук. / Институт металлофизики. – Киев, 1988. – 46 c.
3. Механическая
спектроскопия металлических материалов / Блантер М.С., Головин И.С., Головин
С.А. и др. – М.: МИА, 1994. – 256 c.
4. Новик
А., Берри Б. Релаксационные явления в кристаллах. –М.: Атомиздат, 1975. – 472
c.
5.
Білюк А. І., Зузяк
П. М., Бунтар О. Г. Еволюція структури дисперсійно-твердіючих сплавів після
термоциклювання під навантаженням // Вісник Вінницького політехнічного інституту.
– 1997. – №3. – C. 110-115.
6.
Францевич И.Н.,
Воронов Ф.Ф., Бакута С.А. Упругие постоянные и модули упругости металлов и
неметаллов. – К.: Наукова думка, 1982. – 286 c.
7.
Майєр К.
Физико-химическая кристаллография. – М.: Металлургия, 1972. – 21c.