Строительство и архитектура / 7. Водоснабжение и канализация

К.т.н. Калякин А.М., Чеснокова Е.В., Сауткина Т.Н.

Саратовский государственный технический университет

имени Гагарина Ю.А., Россия

Особенности кинематики течения перед цилиндром при обтекании его открытым потоком.

Формулировка и анализ основных граничных условий.

Приближенный способ решения уравнений движения с привлечением эвристических гипотез.

Изложим алгоритм решения уравнений движения.

Подбираются правдоподобные функции для искомых величин, которые заключают в себе неизвестные числовые коэффициенты. Эти функции удовлетворяют всем граничным условиям, причем удовлетворяют независимо от величины неизвестных постоянных.

На следующем этапе решения все эти функции и их производные подставляются в дифференциальные уравнения движения.

Затем в полученные уравнения подставляются координаты выбранной точки своими числовыми значениями. В результате дифференциальные уравнения движения (их система) переходят в систему алгебраических уравнений относительно неизвестных постоянных.

Решая эту систему, находят значения коэффициентов, ранее неизвестных. И, наконец, подставляя числовые значения теперь уже известных числовых коэффициентов в первоначально заданные функции, получают числовые значения искомых величин в заданной точке.

Основной трудностью при решении задачи является выбор правдоподобных функций, описывающих поле течения (компонент скоростей и давления).

Ниже в качестве примера рассматривается решение задачи об обтекании цилиндра на плоскости ламинарным открытым потоком.

Для наибольшего правдоподобия предполагалось выбирать за основу функции для составляющих скорости при потенциальном плоском обтекании цилиндра идеальной жидкостью.

Для тел, поперечное сечение которых отличается от кругового, возможно найти составляющие скорости, производя преобразование границ кругового цилиндра.

В качестве уравнений движения используем уравнения Навье-Стокса (в цилиндрических координатах).

В качестве основных приближений для скоростей выберем выражение при потенциальном обтекании цилиндра идеальной жидкостью [ 1], рис. 1.

, (1)

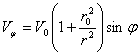, (2)

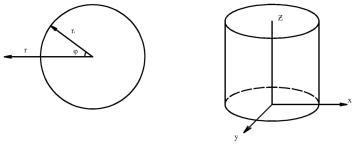
Рис.1.

В отличие от первой части, в которой величиной обозначалась ширина, в котором наблюдалась наибольшая трансформация составляющих и , а составляющая принимала максимальное значение, в данном случае за принято расстояние от оси цилиндра до рассматриваемой точки.

Гарантийные условия для :

при , (3)

при , (4)

при , (5)

при , (6)

Условие (5) при большом удалении перед цилиндром означает, что его влияние мало. Условие (6) при большом числе Re течение близко к потенциальному.

Граничные условия для :

при , (7)

при , (8)

Аналогично, как и для :

при , (9)

при , (10)

Граничные условия для :

при , (11)

при , (12)

при , (13)

при , (14)

где – глубина открытого потока.

В случае ламинарного режима имеем для скорости набегающего потока:

(15)

где - скорость на поверхности, - глубина потока, -расстояние от дня до точки, в которой скорость равна .

Выберем в качестве следующую зависимость:

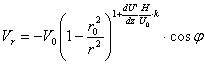(16)

В (16) знак выбран отрицательным, так как направлена против направления отсчета , -неизвестный числовой параметр.

Из (15) имеем:

(17)

Из (16) видно, что при , при , при выражение для совпадает с выражением для составляющей в потенциальном потоке.

В данном случае выражение для скорости является несколько искусственным – это происходит по причине обязательного удовлетворения граничных условий. Неоднозначность способа удовлетворения граничных условий влечет за собой неоднозначность решения, что является основным недостатком предлагаемого в данном случае способа решения уравнений движения.

Литература:

1. Милн-Томсон Л.М. Теоретическая гидродинамика. М.: 1964 – 655 с.

2. Калякин А.М. Метод решения уравнений Навье-Стокса для обтекания препятствий типа мостовой опоры (с использованием эвристических гипотез). Совершенствование методов гидравлических расчетов водопропускных и очистных сооружений: межвуз. науч. сб. Саратов: Сарат. гос. Техн. ун-т, 1996. С. 68-74.