Технические науки/ 2. Механика.

К.ф.-м.н. Нуримбетов А.У., Туреханова Г.И., Жанбосынов Р.С.

Таразский государственный университет им. М.Х.Дулати, Казахстан

Сравнение экспериментальных результатов с теоретическими расчетами кручения, изгиба и растяжения

естественно-закрученных стержней

Применение точной теории естественно-закрученных стержней произвольного поперечного сечения на базе общих уравнений теории упругости связано с большими математическими трудностями и приводят к сложным решениям, и поэтому этот путь для разработки практических методов расчета не рационален. Полученная приближенная теория [1] закрученных слоистых стержней произвольного сечения основана на определенных гипотезах, позволяющих разделить компоненты напряжений и деформаций на главные и второстепенные, которым в ряде уравнений пренебрегается. Достоверность приближенной теории закрученных слоистых стержней проверяется сопоставлением с известными для некоторых частных случаев решениями и сравнением результатов расчетов с экспериментальными данными. Результаты расчета на ЭВМ по линейным соотношениям настоящей работы лучше согласуются с экспериментальными данными, чем существующие в литературе линеаризованные зависимости. Это подтверждает, что предлагаемое кинематическое соотношение (5) [1] полнее отражает взаимовлияние деформации кручения и растяжения.

1. Сравнение экспериментальных результатов с теоретическими расчетами кручения, изгиба и растяжения естественно-закрученных стержней

1.1. Растяжение естественно-закрученных изотропных стержней прямоугольного сечения. Для проверок достоверности основных соотношений технической теории закрученных изотропных стержней, в работе [2] проведен эксперимент на растяжение закрученных образцов прямоугольного сечения из листового дуралюминия Д16АТ, отличающихся шириной а и толщиной h.

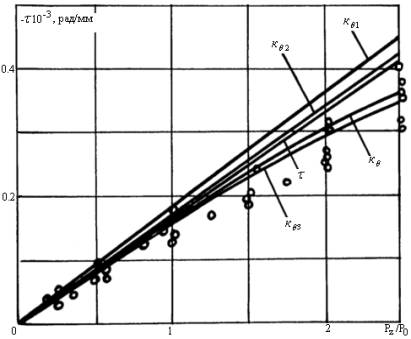
Рис.1.а. Сравнение расчетных углов упругой раскрутки закрученных образцов прямоугольного сечения с экспериментальными (о) значениями. а=30 мм., h=1.45 мм. t₀=0.00197 рад./мм.

При действии только растягивающего усилия Р зависимость t=f(Р) представлена в виде [2] t=-t₀K_qP_q (1), где введены безразмерные параметры

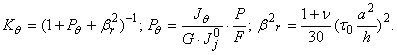(2)

В (2) принято обозначения Здесь устанавливается из определения свойств главного сечения стержня, F- площадь, n - коэффициент Пуассона, а G - модуль сдвига материала сечения.

Линейной теории соответствует значение K_q1=1, технической теории стержня соответствует значение K_q3=(1-b²_r1)^-1, где

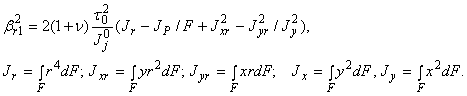(3)

Нелинейной задаче соответствует значение K_q из (2). Расчетные кривые для различных t₀ при указанных значениях коэффициента K_q приведены на рис. 1, знаком (о) указаны экспериментальные результаты.

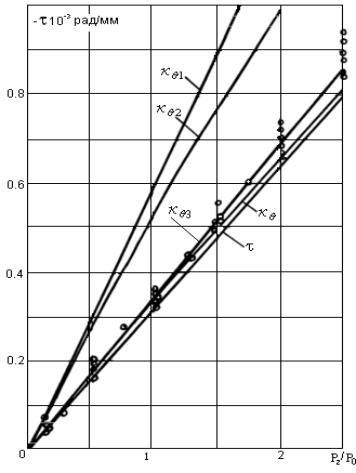
Рис.1б. Сравнение расчетных углов упругой раскрутки закрученных образцов прямоугольного сечения с экспериментальными (о) значениями. а=30 мм., h=1.45 мм. t₀=0.00648 рад./мм.

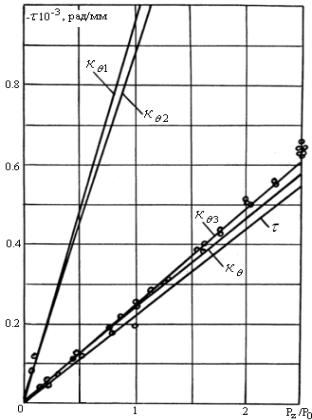
Рис.1с. Сравнение расчетных углов упругой раскрутки закрученных образцов прямоугольного сечения с экспериментальными (о) значениями. а=30 мм., h=1.45 мм. t₀=0.013 рад./мм.

Видно хорошее соответствие результатов расчета по соотношениям (15) [1] в широком диапазоне изменения упругой раскрутки t. В работе [3] формула (2) представлена в качестве руководства при расчете на прочность рабочих лопаток ГТД.

1.2. Растяжение, изгиб и кручение закрученных слоистых стержней прямоугольного сечения, составленных из ортотропных материалов.

Л.А.Горшковым проведена серия экспериментов над закрученными образцами прямоугольного сечения из стеклопластика и углепластика с различными вариантами укладки слоев. Образцы шириной 40 мм., длиной 100 мм. и углом закрутки 30° при различных толщинах подвергали растяжению. Варьируя толщину образцов, была получена экспериментальная зависимость угла упругой раскрутки от толщины h (рис. 2). В связи с близостью значений углов раскрутки различных образцов на рис. 2 приведена экспериментальная кривая только для стеклоткани, расположенной основой вдоль оси образца. На этом же рисунки приведена теоретическая кривая, рассчитанная по формуле (15) [1]. Упругие константы стеклоткани и стеклопластика ТЖС-0.7 близки и поэтому справедливо утверждение, что экспериментальные точки ложатся довольно близко к расчетным кривым.

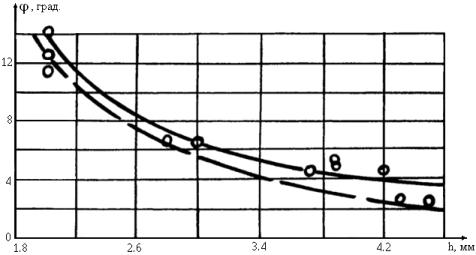
Рис.2. Сравнение расчетных (пунктирная линия) значений угла упругой раскрутки закрученных образцов прямоугольного сечения из стеклоткани при растягивающей нагрузке 5900 Н с экспериментальной кривой (сплошная линия). (о) - экспериментальные точки.

Для образцов из углепластиков, армированных под углом 0°, зависимости угла раскрутки от растягивающей силы приведены на рис. 3. На этом же рисунке нанесена прямая, соответствующая теоретическим расчетам по формуле (15) [1]. Видно, что соответствие экспериментальных и теоретических данных достаточно хорошее.

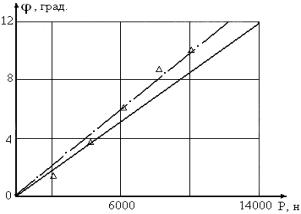
Рис 3. Сравнение расчетных (сплошная линия) значений угла раскрутки для однонаправленных образцов прямоугольного сечения из углепластика с экспериментальной кривой в зависимости от нагрузки. Пунктирная линия - кривая, построенная по экспериментальным точкам ().

Таким образом, результаты сравнения экспериментальных данных с теоретическими расчетами подтверждают правильность вывода соотношений (15) [1]. Соотношение (15) [1] применяется в некоторых задачах техники, связанных исследованиями прочности воздушных винтов, лопастей вентиляторов, лопаток паровых турбин и т.д.

Литература:

1. Нуримбетов А.У., Туреханова Г.И., Жанбосынов Р.С. Деформация естественно-закрученных многослойных анизотропных стержней при кручении и растяжении // Materiály IX mezinárodní vědecko - praktická konference «Moderní vymoženosti vědy – 2013». - Díl 73. Technické vědy: Praha. Publishing House «Education and Science» s.r.o - 96 stran, С.17-22.

2. Шорр Б.Ф. К экспериментальной проверке теории растяжения закрученных стержней //Изв. АН СССР. Механика твердого тела.- 1972.-№5.-С. 147-153.

3. Биргер И.А. Пространственное напряженное состояние в лопатках с начальной закруткой. //Тр. ЦИАМ. - 1982. - № 996, с. 7-23.