Лагуткин М.Г., Исаев С.В., Михальченкова А.Н.

Московский государственный машиностроительный университет (МАМИ), Институт инженерной экологии и химического машиностроения, факультет химико-технологического оборудования

Исследование работы вихревого эжектора с помощью компьютерного моделирования.

Вихревой эжектор при малых габаритах и простоте конструкции получил распространение в различных отраслях промышленности. Однако отсутствие единой надежной методики расчета вихревых эжекторов сдерживает их использование в промышленности. Но явно выявленные достоинства вихревых эжекторов заставляют исследователей и в наше время осуществлять попытки изучения работы вихревых эжекторов с целью создания расчетных зависимостей для определения основных характеристик работы аппарата и его конструктивных и режимных параметров.

В настоящее время кроме использования лабораторных стендов с целью практического исследования работы тех или иных аппаратов имеется возможность компьютерного моделирования конструкции аппарата и дальнейшего исследования гидродинамической картины внутри созданной модели. Качественная реализация поставленной задачи может быть осуществима с помощью пакета программ SolidWorks, с помощью которого на начальном этапе создается трехмерная модель аппарата, в нашем случае вихревого эжектора, а в дальнейшем с помощью встроенного пакета программ COSMOSFloWorks исследуется влияние конструктивных и режимных параметров на величину коэффициента эжекции. Такой подход позволяет провести исследование вихревого эжектора в различных его конструктивных исполнениях и на основании многочисленных экспериментальных данных определить связь между основными параметрами аппарата с целью определения математической зависимости для их расчета.

Исследование вихревого эжектора с помощью компьютерного моделирования способно значительно сократить затраты времени на проведение испытаний, связанных с изучением влияние тех или иных параметров на величину коэффициента эжекции. Моделирование турбулентного течения жидкости в COSMOSFloWorks осуществляется с помощью осредненных по Рейнольдсу системы уравнений Навье-Стокса. Кроме того используются уравнения состояния компонентов текучей среды, а также эмпирические зависимости вязкости и теплопроводности этих компонентов среды от температуры. Для замыкания системы уравнений используются уравнения переноса кинетической энергии турбулентности и ее диссипации в рамках k – ε модели турбулентности.

Расчетная схема вихревого эжектора, созданная в программе SolidWorks для расчета в COSMOSFloWorks, представлена на рис. 1. Модель соответствует схематическому изображению вихревого эжектора, который работает следующим образом: рабочий (эжектирующий) поток газа подается в цилиндрический корпус 1 аппарата через тангенциально расположенные патрубки 2 и закручивается, на оси аппарата создается разряжение при увеличении давления во вращающемся потоке газа по направлению к стенкам корпуса, в результате чего становится возможным подсос газа через патрубок входа эжектируемого потока 3, расположенный коаксиально цилиндрическому корпусу 1 аппарата со стороны входа рабочего потока, внутри аппарата рабочий и эжектируемый потоки газа смешиваются и выходят через тангенциальный патрубок выхода смешанного потока 4, расположенный с противоположной стороны аппарата.

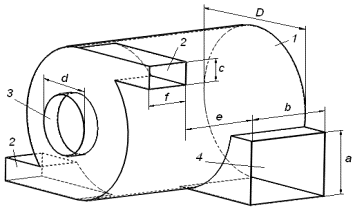
Рис. 1. Расчетная схема вихревого эжектора.

1 – цилиндрический корпус, 2 – патрубки входа рабочего потока, 3 – патрубок входа эжектируемого потока, 4 – патрубок выхода смешанного потока.

Основной характеристикой работы вихревого эжектора является коэффициент эжекцииu, который представляет собой отношение расходов эжектируемого и рабочего потоков газа.

Основной задачей при исследовании модели аппарата является определение влияния конструктивных и режимных параметров работы вихревого эжектора на величину коэффициента эжекции. К основным конструктивным параметрам могут быть отнесены размеры патрубков входа рабочего потока 2 (рис. 1), патрубка входа эжектируемого потока 3, патрубка выхода смешанного потока 4 и длина цилиндрического корпуса 1 аппарата. Кроме того на величину коэффициента эжекции могут оказывать влияние конструктивные особенности патрубков входа рабочего потока и патрубка выхода смешанного потока, а именно отношение длины и ширины их поперечного сечения. К основным режимным параметрам относятся скорость газа в патрубках входа рабочего потока и величина наружного давления перед патрубками входа эжектируемого потока и выхода смешанного потока. Также на величину коэффициента эжекции могут оказывать влияние свойства (плотность, вязкость) эжектируемого и рабочего потоков газа.

Зависимость коэффициента эжекции от приведенных выше параметров можно записать в следующем виде:

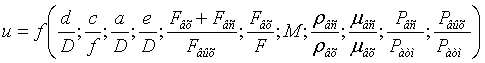. (1)

где u – коэффициент эжекции, d – диаметр патрубка входа эжектируемого потока, D – диаметр цилиндрического корпуса аппарата, c – ширина поперечного сечения патрубков входа рабочего потока газа, f – длина поперечного сечения патрубков входа рабочего потока газа, a – ширина поперечного сечения патрубка выхода смешанного потока, e – расстояние от нижней кромки тангенциальных патрубков входа рабочего потока 2 до верхней кромки тангенциального патрубка выхода смешанного потока4, F_вх – площадь поперечного сечения патрубков входа рабочего потока газа 2, F_вс – площадь поперечного сечения патрубка входа эжектируемого потока 3, F_вых – площадь поперечного сечения патрубка выхода смешанного потока 4, F – площадь поперечного сечения цилиндрического корпуса 1 аппарата, M – число Маха в патрубках входа рабочего потока газа 2, ρ_вс – плотность эжектируемого потока газа, ρ_вх – плотность рабочего потока газа, μ_вс – динамическая вязкостьэжектируемого потока газа, μ_вс – динамическая вязкость рабочего потока газа, P_вс – наружное давление перед патрубком входа эжектируемого потока, P_атм – атмосферное давление, P_вых – наружное давление перед патрубком выхода смешанного потока.

В ходе проведения работы было принято решение некоторые из исследуемых параметров представить в том значении, которое обеспечивает максимальную величину коэффициента эжекции. К таким параметрам были отнесены конструктивные особенности патрубков входа рабочего потока и выхода смешанного потока, а именно отношение ширины поперечного сечения патрубка входа рабочего потока к его длине c/f и отношение ширины поперечного сечения патрубка выхода смешанного потока к диаметру аппарата a/D. Кроме этого была найдена рациональная величина длины цилиндрического корпуса аппарата. Представленные конструктивные параметры принимают следующие рациональные значения, которые принимаются в качестве постоянных величин: c/f=0,4, a/D=0,5 и e/D=0,5.

Математическое моделировании процесса эжекции газа в вихревом эжекторе при условии атмосферного наружного давления перед патрубками входа эжектируемого потока и патрубком выхода смешанного потока.

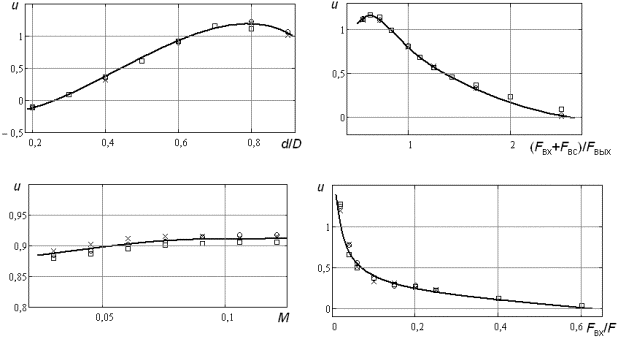
Рис. 2. График зависимости коэффициента эжекцииот:

а – отношения диаметра патрубка входа эжектируемого потока к диаметру цилиндрического корпуса аппарата,

б – отношения суммарной площади поперечного сечения патрубков входа рабочего потока и патрубка входа эжектируемого потока к площади поперечного сечения патрубка выхода смешанного потока,

в – числа Маха в патрубках входа рабочего потока,

г – отношения площади поперечного сечения патрубков входа рабочего потока к площади поперечного сечения цилиндрического корпуса аппарата.

На рис. 2(а-г) представлены графики зависимости величины коэффициента эжекции от основных конструктивных параметров работы вихревого эжектора и от числа Маха (рис. 2г) в патрубках входа рабочего потока газа. Рациональные интервалы значений исследуемых величин определяются с учетом того, что коэффициент эжекции должен принимать положительные значения вплоть до максимально возможной величины. На графике, изображенном на рис. 2а, коэффициент эжекции обращается в ноль при величине d=0,25D и принимает максимальное значение при d=0,8D. На рис.2б при F_вх+F_вс=2,5F_выхкоэффициент эжекции обращается в ноль, при этом значение F_вх+F_вс=0,67F_вых обеспечивает максимальную величину коэффициента эжекции. На рис. 2в наблюдаем, что при значении скорости газа в патрубках входа рабочего потока выше 30 м/с (M=0,09) коэффициент эжекции перестает расти, но при этом будет расти гидравлическое сопротивление. На рис. 2г коэффициент эжекции обращается в ноль при значении F_вх=0,6Fи при F_вх<0,1Fначинает заметно увеличиваться, но при этом в случае создания избыточного давления внешней среды на выходе из аппарата величина коэффициента эжекции при малых площадях поперечного сечения патрубков входа рабочего потока будет резко падать. Кроме того, с уменьшением площади поперечного сечения патрубков входа рабочего потока газа при неизменном значении скорости газа будет снижаться его расход, что приведет к снижению расхода эжектируемого газа. На основании опытных данных при значении F_вх>0,3Fрасход эжектируемого потока перестает расти, а при F_вх<0,05F наблюдается резкое снижение расхода эжектируемого потока.

В результате исследования графиков, изображенных на рис.2(а-г) можно сделать вывод, что работа вихревого эжектора будет наиболее рациональна при следующих значениях конструктивных и режимных параметров: d=(0,25-0,8)D, F_вх+F_вс=(0,67÷2,5)F_вых, M<0,09 и F_вх=(0,05-0,3)F.

На рис. 3(а) представлен график зависимости коэффициента эжекции от отношения плотности эжектируемого потока газа к плотности рабочего потока. На рис. 3(б) изображен график зависимости величины коэффициента эжекции, исключающей влияния плотности газовых потоков, от отношения вязкости эжектируемого и рабочего потоков газа. На графике видно, что при использовании в аппарате газов с одинаковой плотностью, но различной вязкостью, величина коэффициента эжекции практически не изменяется, поэтому влиянием вязкости газа можно пренебречь.

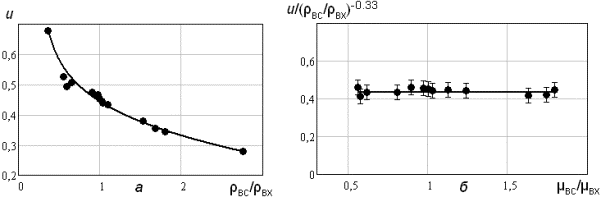
Рис. 3. График зависимости величины коэффициента эжекцииот:

а – отношения плотности эжектируемого потока газа к плотности рабочего потока;

б – отношения вязкости эжектируемого потока газа к вязкости рабочего потока (величина коэффициента эжекции исключает влияние плотности потоков газа, доверительный интервал составляет ±5%).

В результате зависимость (1) с учетом того, что отношения c/f, a/D и e/D принимаются в качестве постоянных величин, можно представить в виде уравнения:

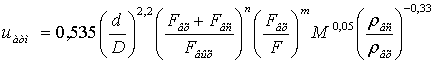, (3)

где n=-1,56при F_вых=(0,6-0,9)(F_вх+F_вс),n=-1,21при F_вых=(0,9-1,2)(F_вх+F_вс),n=-1,02при F_вых=(1,2-1,5)(F_вх+F_вс),m=-0,7при F_вх=(0,07-0,25)F, m=-0,3при F_вх=(0,25-0,5)F.Уравнение получено с учетом, чторасстояние от нижней кромки патрубков входа рабочего потока до верхней кромки патрубка выхода смешанного потока e=0,5D, ширина поперечного сечения патрубка выхода смешанного потока a=0,4D, ширина поперечного сечения патрубков входа рабочего потока c=0,4f.