А.В. Кривошейкин д.т.н., профессор зав. кафедрой СПбГУКиТ

М.А.Чесноков, аспирант СПбГУКиТ

Получение произвольной длины линии задержки в цифровом гребенчатом фильтре на основе интерполяционного многочлена Лагранжа

В ряде радиотехнических систем [1] используются периодические сигналы с периодом τ, для обработки которых применяются гребенчатые фильтры (ГФ). Выходной сигнал ГФ формируется как сумма входного сигнала и выходного сигнала, задержанного на время τ и умноженного на коэффициент обратной связи g < 1. Гребенчатый фильтр является многополосным фильтром, амплитудно-частотная характеристика (АЧХ) которого достигает максимумов на частотах 0, 1/τ, 2/τ, …, n/τ, где n – натуральное число [2], соответствующее номеру полосы пропускания ГФ. Гребенчатый фильтр используется в качестве фильтра, согласованного с периодическим сигналом, при этом частоты максимумов в спектре сигнала совпадают с частотами максимумов АЧХ ГФ.

При цифровой реализации ГФ находящиеся в линии задержки числа представляют собой выборки значений выходного сигнала, а соседние значения разделяются интервалом времени равным периоду дискретизации системы Δτ. Таким образом, сигнал на выходе линии задержки ГФ может быть задержан относительно сигнала на выходе ГФ только на интервалы времени кратные периоду дискретизации системы. Если это условие не выполняется, т.е. τ ≠ nτ_д, где n – натуральное число, то частоты максимумов АЧХ ГФ не совпадают с частотами максимумов в спектре сигнала. Более того, гребенчатый фильтр вместо подавления помех начинает выделять спектральные составляющие помех, отсутствующих в полезном сигнале.

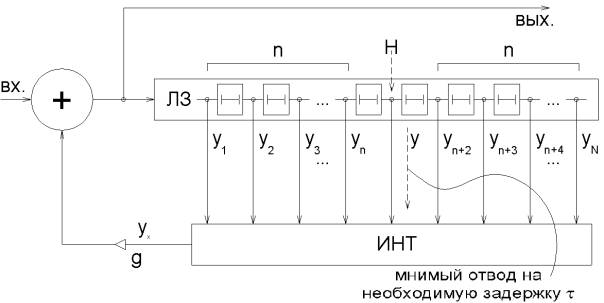
Рис.1. структурная схема гребенчатого фильтра с линией задержки продолжительностью в дробное число отсчетов.

Структурная схема для данной системы представлена на рис. 1. Пусть необходимое время задержки ГФ τ не равно целому числу периодов дискретизации Δτ. Необходимо найти оценку значения сигнала в линии задержки y(τ).

Для этого, сначала определяется ближайшее целое к значению задержки τ в периодах дискретизации. Ближайшее целое значение обозначим H. Возьмем выборку в n отсчетов до и после H общей длиной N=2n+1. Значения задержки отсчетов сигнала в линии обозначим как τ₁, τ₂,… τ_N. Соответствующие им значения сигнала из линии задержки y₁,y₂,…y_N.

Чтобы найти оценку значения сигнала соответствующие задержке τ необходимо решить интерполяционную задачу, производимую блоком ИНТ на рис. 1. Интерполируем значения сигнала внутри выборки степенным полиномом (N-1) ой степени

y(τ) = a_N-1τ^N-1+ a_N-2 τ^N-2+… +a₀ τ⁰ _. (1)

Для нахождения коэффициентов a_N-1, a_N-2,…,a₀ необходимо решить систему линейных уравнений:

Т.к. τ₁, τ₂,… τ_N заранее известны и все отличны друг от друга, т.о. определитель главной матрицы всегда не равен нулю. Расчёт коэффициентов путём непосредственного решения системы уравнений даже при малом порядке системы может привести к большой погрешности их значений [3], поэтому следует использовать одно из ряда явных представлений интерполяционного многочлена, например, интерполяционный многочлен Лагранжа:

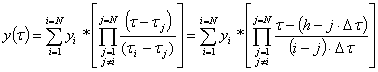, (2)

где h = Δτ*entire(τ/Δτ).

Блок ИНТ, представленный на рис.3, производит расчёт сигнала на его выходе по формуле (14).

Цифровая реализация гребенчатого фильтра в качестве приёмника, согласованного с периодическим сигналом, требует решения проблемы дискретности линии задержки, приводящей к отклонению АЧХ сигнала от АЧХ гребенчатого фильтра. В статье предложен метод интерполяции, основанный на использовании дискретных значений отсчётов сигнала, ближайших к заданному значению.

Список литературы:

1. Финкельштейн М. И. Гребенчатые фильтры. М., «Советское радио», 1969, 320 стр.

2. Финкельштейн М. И. Основы радиолокации: Учебник для вузов. — 2-е Ф59 изд., перераб. и доп. — М.: Радио и связь, 1983.

3. Березин И.С., Жидков Н.П. Методы вычислений. Т.1.- М.: Наука, 1966.