Иванов С.
В., Корноухова Е. С.
Донской
государственный технический университет, Россия
Разработка алгоритма оптимально-терминального
управления беспилотным летательным аппаратом в конфликтной задаче
Рассмотрен
подход, позволяющий cформировать
субоптимальную стратегию игрока-союзника в нелинейной задаче позиционного
управления с обратной связью, возможную для реализации в реальном времени.
Известные методы теории дифференциальных игр,
используемые для управления маневрами
уклонения высокодинамичных объектов, традиционно не позволяют учитывать терминальные
ограничения на векторы фазовых координат игроков. Вследствие этого, ошибки
приведения объекта-союзника в заданную терминальную область в некоторых
практических приложениях могут быть значительными.
Рассмотрен метод управления беспилотным
летательным аппаратом (БЛА) (союзником) от средств противника, обеспечивающий
не только совершение маневра уклонения, но и выведение БЛА в заданную
терминальную область пространства с требуемой точностью.
Предполагается, что союзнику ничего неизвестно о
текущем состоянии противника, тогда как противнику текущее состояние
игрока-союзника известно точно. За исключением принято, что объекту-союзнику
известны начальный момент времени реализации игры, начальные условия функционирования
свои и противника, а также физические возможности обоих игроков.
Отличительной особенностью синтезируемого
управления является то, что использован модифицированный алгоритм решения
двухточечной краевой задачи, сводящий ее к задаче Коши и учитывающий
терминальные ограничения.
Рассмотрен
практический пример синтеза управления маневром уклонения гипотетического БЛА,
иллюстрирующий эффективность использования разработанного метода в реальных
системах.
Дифференциальные
уравнения, описывающие движение союзника и противника: 
Условие минимакса: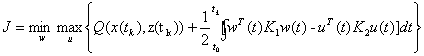 
, где 
- расстояние между противником и союзником,
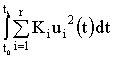и
-
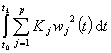оптимальные допустимые
стратегии управления u0(t) и w0(t),
K 1, K 2 –
симметричные положительно определенные матрицы соответствующих размерностей.
Полагается, что
противник формирует замкнутое управление по принципу обратной связи
"наихудшим" образом: 
Ограничения
на управление: 
.
Общий
вид гамильтониана для нашей задачи:
.
Применим
метод максимума Понтрягина, который приведет к получению двухточечной краевой
задачи (ДТКЗ):
Для решения
сформированной двухточечной краевой задачи (ДТКЗ) целесообразно воспользоваться
методом сведения ДТКЗ к одноточечной задаче Коши, изложенным в работе Баркова и
Кочеткова [3].
После
решения ДТКЗ предлагается нахождение управления в замкнутом контуре системы
оптимально-терминального управления.
Структура
терминальной СУ представлена на рисунке 1.
Сущность его заключается в следующем: по
текущей навигационной информации определяются начальные условия 
(
– номер итерации решения задачи в медленном контуре) и в
медленном контуре
прогнозируется
субоптимальная траектория 
на последующий
интервал движения ЛА 
(
, 
).
Разработанная
структура терминальной СУ, реализующей метод терминального управления позволила
получить управление в форме синтеза за счет увеличения такта решения задачи
управления в медленном контуре.
