Ecology / 6. Environmental Monitoring
Ph.D. Proskurnin OA, Smirnov
SA
Scientific - Research
Institution “Ukrainian Scientific Research Institute of Ecological Problems”,
Ukraine
Ph.D. Rybalova OV, Ph.D. Belan
SV
National University of Civil
Defense of Ukraine
Using Monte
- Carlo method for assessment of environmental risk caused by wastewater
discharges into a watercourse
One of
the biggest environmental problems in economically developed countries is a contamination
of water bodies (WB) by industrial, field, agricultural and municipal
wastewater (WW). In a number of post-Soviet countries, particularly in the
Russian Federation and Ukraine, in order to provide the contamination level
above the safe one it is developed and approved standards of pollutants discharge.
The standard of pollutants discharge is a limit mass of the substance, which is
allowed to discharge into WW per unit time [1, 2].
Elaboration
of the standard of pollutants discharge includes the calculation of allowable WW
amount. The calculation is based on the assessment of WB condition at a fixed
level of contamination. In the first phase the actual level of contamination is
validated. A disadvantage of the current approach to solving this problem is
the neglecting probabilistic nature of the content of pollutants in WW withdrawing
into WB. In methodological literature instability of WW is determined only by
the requirement to take into account an arithmetic mean value as the actual
concentrations of substances [3, 4]. (In order to increase representativeness
of the observation samples Ukrainian methodology [3] requires before averaging the
concentrations exclude the minimum and maximum values). Overall, however, the
calculation is rather deterministic: it defines the permissible concentration of
substances in WW which, according to calculation, does not lead to exceeding
the legally approved maximum of permissible concentration (MPC) of the
substances in WB. Thus, to include the consideration of the probabilistic
nature of WW is actual, as well as to consider the parameters of the
probabilistic nature of WB condition in the zone of discharge influence. This
will increasingly allow reflect the real nature of the process WB contamination.
The
most perspective direction in solving this problem seems to be the usage of ecological
risk assessment mechanism. According to the classical definition, risk is a
measure of uncertainty, which can be assessed by probabilistic method [5] In
practice, we use different criteria of this uncertainty. In most cases as an
environmental risk we understand either the risk of adverse changes in the environment,
or expectation of damage due to such changes [6]. Since in the rationing sanitation
problems only a possible fact of exceeding the MPC in WW is taken into account without
the analysis of its consequences for ecosystems and humans, it is advisable to
use the first definition of environmental risk, i.e. to consider the risk as a
probability of violation of environmental quality standards of WB due to WW
discharge.
In [7]
a method for calculating the permissible concentrations of substances in WW by
environmental risk assessment is described. However, described mechanism was
based on a significant assumption, that the concentration of the substance in
WW regarded as a random variable is distributed according to the normal law.
But this is true only if the process of formation of WW compounds is affected approximately
by equivalent factors [8]. In the case of sanitation (including water treatment),
this condition can not be met, and therefore it is necessary to provide an
arbitrary law of substance concentration distribution of in WW. For this purpose
a universal Monte Carlo method can be used, which was previously used to
determine the risk of technogenic accidents at potentially hazardous facilities
[9]. In this paper we consider the use of Monte Carlo method for estimation of
the probability of exceeding the MPC in WB below the WW discharge. The problem
is considered on the example of a conservative pollutant.
The
basis of the Monte Carlo method is based on the following mathematical
regularity [10]. If there is a random variable x, then its distribution function F(x) can also be considered as a random variable. In this case,
regardless to the law of initial value x
distribution the value of F(x) is
uniformly distributed on the interval [0 , 1]. This implies that the possible
values x may be derived from the equation
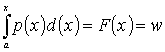 , (1)
, (1)
where a is lower boundary of
determining the value x; p(x) is density of distribution; wÎ [ 0 , 1] - uniformly distributed random
variable .
Equation
(1 ) of each realization of the random variable wÎ [ 0, 1 ] puts in one correspondence the
realization of x , distributed
according to given law F(x). This
allows to simulate the behavior of a random variable x by generating a random number value w.
Applied
to the problem of environmental risk assessment this pattern can be used as
following. If we represent a risk indicator I
as a function ![]() and generate several
times the value wiÎ [0, 1], i=1÷N, by the sample
and generate several
times the value wiÎ [0, 1], i=1÷N, by the sample ![]() we can judge
about the distribution of I. In particular
, the sample allows to calculate the non-exceedance probability of a given
value .
we can judge
about the distribution of I. In particular
, the sample allows to calculate the non-exceedance probability of a given
value .
In this
problem as a risk indicator serves the concentration
of conservative substance in control section (CS) , which is expressed by a
balance equation
![]() , (2)
, (2)
where Сфон, С, Скс is concentration of the substance in the
background section respectively (BS ) above WW discharge, in WB and in ; Qфон, q - , respectively is a water flow rate in the BS and WW flow rate.
Concentration
of C in the right side of equation ( 2) is a random variable which may
be represented as an argument of the distribution function , i.e. as. w- quantile (Fig. 1) .
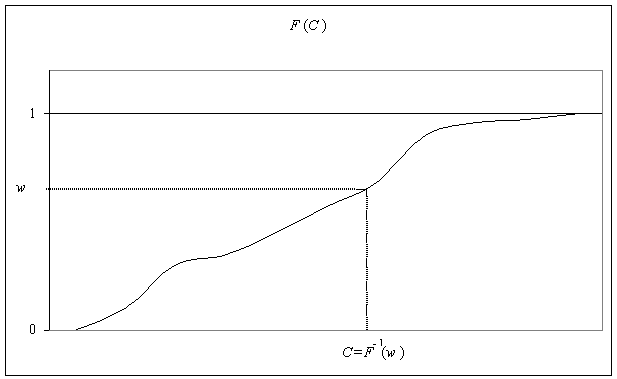
Figure
1 - Representation of the C concentration
in the form w- quantile
In this
case, the risk indicator is presented as a function of w:
![]()
where F-1
- is the inverse function of the
distribution function F(C).
In
practical problems, the function F(C)
can be constructed empirically according to field observations, followed by smoothing.
Below
is a demo, which is based on developed and approved standard of municipal WW discharge
in Alushta (Crimea) in the river Ulu Uzen (small river of Crimea) [11]. As an
indicator of pollution in this example ammonia nitrogen is considered. Table 1
shows the content of the substance in WW after refining at biological
wastewater treatment plants.
Table 1
- The content of ammonia nitrogen in municipal WW in Alushta in 2009
|
Month of Year |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Concentration
of C , mg/dm 3 |
0,86 |
0,79 |
0,62 |
1,20 |
0,65 |
0,62 |
0,52 |
0,78 |
0,61 |
0,74 |
0,77 |
0,78 |
Design
conditions for determination of ammonia nitrogen maximum concentration in WW has
been adopted as the following [11] :
- Water
flow in the FS Qфон = 0.03 m3 / s;
- WW flow
q = 0,02 m3 / s;
- concentration
of ammonia nitrogen in the FS Qфон = 0.05 dm 3 ;
- MPC of
ammonia nitrogen (at the moment of standards elaboration) 0.39 mg/dm 3.
In the
paper [11], the calculation of allowable concentration was conducted in
accordance with the existing procedure [3] excluding the probabilistic nature
of the substance concentration in WB and without environmental risk assessment
. As allowable concentration it was adopted estimated actual concentration
(mean value, excluding the maximum and minimum values) , equal to C = 0.720 mg/dm 3. Adoption
of the actual concentration as permissible due to the fact that the
concentration does not result in exceeding the maximum permissible
concentration in CS. Due to the short distance between the WW discharge and the
CS we can neglect the water self-cleaning. Then the concentration of the
substance in the CS is
![]()
In
order to assess the environmental risk on the base of Table 1 it was built the
empirical distribution function F(C)
followed by a linear smoothing (Fig. 3) . Level of risk acceptability is
assumed to be 0.05.
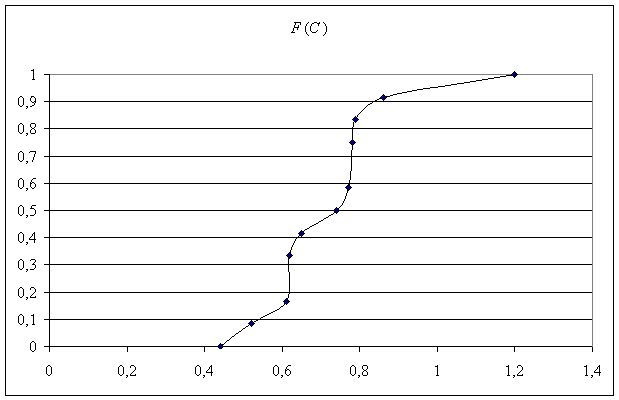
Figure
3 - The empirical probability distribution function of the concentration C
The
result of calculation of the random variable Скс for N =
10000 is the following : in 91115 cases Скс £MAC; in other cases
- Скс > MPC. Thus, the probability that
the concentration of ammonia nitrogen in the CS will exceed MPC makes
(10000-91115) / 10000 » 0,09. Consequently, the value
of considered environmental risk exceeds acceptable level .
Fig . 4
shows a histogram of the value Скс
distribution.
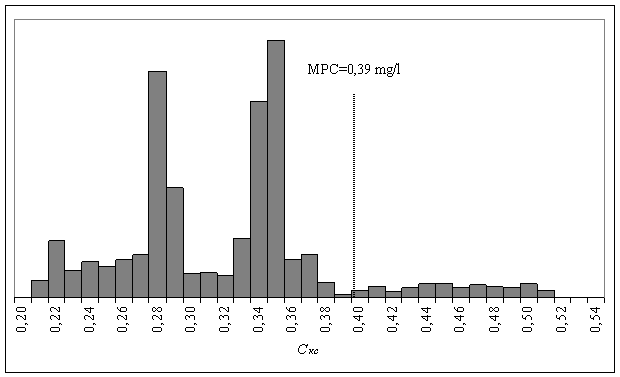
Figure
4 - Histogram of the value Скс
distribution
Conclusion.
The proposed algorithm for environmental risk assessment, which is based on the
Monte Carlo method , allows us to calculate the probability of non-exceedance
concentration level of a substance in the WB in the zone of WW discharge influence.
In speculating process the law of concentration distribution in the WW was taken
arbitrary , the method of risk assessment can be attributed to the
non-parametric .
It
should be noted that the adoption of an acceptable level of pollution in MPC is
not critical in terms of the calculation algorithm. As the acceptable level of
contamination it can be accepted an environmental standard for water bodies,
which is defined as the upper limit of the third category of water quality according
to the classification of surface water quality [12].
Subject
for further research is the complication of the problem in terms of assessing
the WW discharge influence directly on human health.
Bibliography:
1. Водный кодекс
Украины. К., Издательский Дом “Ін Юре”, 2004. – 138 с.
2. Водный кодекс РФ //
zakonrf.info/vodniy-kodeks/.
3. Инструкция о
порядке разработки и утверждения предельно-допустимых сбросов (ПДС) веществ в
водные объекты с возвратными водами. – Харьков: УкрНЦОВ, 1994. – 79 с.
4. Методика разработки нормативов допустимых сбросов веществ и
микроорганизмов в водные объекты для водопользователей // http://www.mnr.gov.ru/regulatory/detail.php?ID=21179.
5. Лисиченко Г.В.,
Хмель Г.А., Барбашев С.В. Методология оценивания экологических рисков / Г.В.
Лисиченко, Г.А. Хмель, С.В. Барбашев – Одесса: Астропринт, 2011. – 368 с.
6. Khigt F. Uncertainty
and Profit. – Boston: Houghton Miffin Co, 1921. – P. 210 – 235.
7. Проскурнин О.А.
Нормирование состава сточных вод путем оценки экологического риска / О.А.
Проскурнин // Вода и экология: проблемы и решения. – С.Пб., ООО «Борвик полиграфия», 2013. – № 4. – С. 65–73.
8. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А.
Практикум по теории статистики. — 3-е изд. — М.: Финансы и
статистика, 2011. — 416 с.
9. Бойко Т.В. Визначення техногенного ризику на основі методу Монте-Карло /
Т.В. Бойко, І.Р. Батуринська // Восточно-Европейский журнал
передовых технологий – № 2/11 – 2013 – С. 4-6.
10.
Ермаков С.М. Метод Монте-Карло и смежные вопросы. – М.: Наука, 1975. –
472 с.
11.
Отчет о НИР «Разработка норм ПДС
нормированных веществ со сточными водами КРП "ППВКХ г.Алушты" в водные
объекты"». УкрНИИЭП,
Харьков, 2009 – 63 с.
12.
Методика екологічної оцінки якості поверхневих вод за відповідними
категоріями [Текст]/ В.Д. Романенко,
В.М. Жукинський, О.П. Оксіюк та ін.– К.: Символ-Т, 1998. – 28 с.