Бронштейн Е.М., доктор физико-математических наук, профессор кафедры вычислительной математики и кибернетики, Уфимский государственный авиационный технический университет, профессор.

Исхаков Ф.Р., аспирант кафедры вычислительной математики и кибернетики, Уфимский государственный авиационный технический университет Инженер-программист ООО НПФ «Экситон-автоматика»

Оптимизация смешанного двухуровневого договора перестрахования на основе комбинированного показателя

Любое страховое общество даже при тщательном отборе рисков при приеме их на страхование не может создать портфель полностью изолированных друг от друга объектов страхования [1, c.184]. Возникает потребность в страховании своих активов в других страховых компаниях. Соответственно страховой компании необходимо заключать договор перестрахования.

В данной работе рассматривается комбинированный двухуровневый договор перестрахования, включающий в себя элементы эксцедентного и квотного видов перестрахования. Задача перестрахования заключается в оптимизации параметров этого договора по ряду критериев.

1. Методика принятий решений

Страховой компании необходимо выбрать из множества возможных договоров перестрахования (стратегий) наиболее эффективный. Для решения данной задачи был использован метод анализа иерархий. Проблема выбора отражена в виде иерархии, содержащей три уровня: цель, критерии и альтернативы (рис.1). Под альтернативами понимаются различные договора перестрахования. В качестве критериев выбраны меры риска VaR^a и CVaR^a случайной величины – убытка страховщикаDU^a =U₀ – U₁^α, где U₀, U₁^a– соответственно начальный и конечный (при использовании стратегии a) капитал инвестора, вероятность разоренияP^a, математическое ожидание прибылиM^a.

VaR^a —величина ущерба, которая с вероятностью, равной уровню доверия φ= 0,95, не будет превышена:

VaR^a_φ [DU^a] = inf {ξ | P(DU^a ≤ ξ ) ≥ φ}.

CVaR^a—математическое ожидание убытка компании при условии, что его величина большеVaR^a:

CVaR^a_φ [DU^a] = E[DU^a | DU^a ≥ VaR(DU^a)].

M^a— математическое ожидание прибыли страховой компании:

M^a= E[ U₁^a – U₀].

P^a—вероятность разорения страховой компании:

P^a= P[ U₁^a< 0].

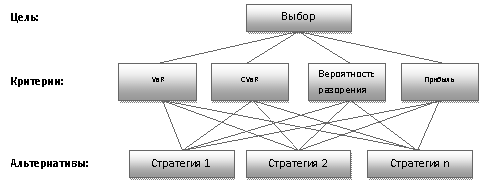
Рис.1. Структура задачи выбора решения.

Оценка договоров основана на вычислении комбинированного показателя для каждой из рассматриваемых стратегий. Комбинированный показатель будем искать в виде выпуклой комбинации [2,c.92]

, (1)

где λ_i^α— нормированное значение i-го критерия, ω_i — весовые коэффициенты, α — стратегия (вид договора перестрахования). Предпочтительна стратегия с минимальным значением Θ^α.

Величины весовых коэффициентов ω_i определяется пользователем: чем предпочтительней критерий, тем больше значение коэффициента. Весовые коэффициенты удовлетворяют следующим условиям:

.

Случайные величины: мера риска VaR^a, CVaR^a, P^a, M^a имеют разную размерность, т.е. их значения несопоставимы. Поэтому при формировании комбинированного показателя целесообразно вместо каждой из случайных величин X_i^a (i=1,2,4 – кроме P^a) рассматривать величины, нормированные следующим образом. Считаем, что значения X_i^a являются случайными величинами, зависящими от стратегии a [3,c.75]

,

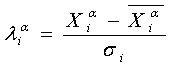где ― математическое ожидание X_i^a, σ_i ― среднее квадратическое отклонение случайной величины X_i^a.

2. Договор перестрахования

С точки зрения страховой компании, договор перестрахования представляет собой функцию, где размер иска является независимой переменной y, сумма компенсации страховой компанией – зависимой переменной F_ψ(y). Мы рассматриваем функцию, которая зависит от четырех параметров и является сочетанием эксцедентного и квотного видов перестрахования [4,c.300], причем рассмотрены две «квотные» области (двухуровневая модель).

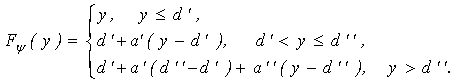⁽¹⁾

Функция перестрахования для перестраховочной компании выглядит следующим образом:

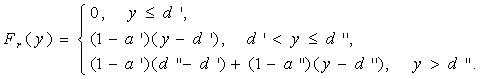
Здесь a’, a”<1, стратегия задается параметрами a’, a”, d’, d”. Разумеется, F_ψ(y) +F_γ(y) = y.

3. Формирование капитала страховой компании

U₁ – капитал страховой компании в конечный момент времени вычисляется следующим образом:

U₁ = U₀+ Pr + I – L – E – R – T ,

Где U₀ – начальный капитал компании, Pr – премии, I – доход компании от инвестиционной деятельности, L – страховые выплаты с учетом перестрахования, E – расходы, R – сумма премий, выплачиваемая перестраховщику, T – налоги.

4. Результаты вычислений

Математическая модель реализована в программном продукте, с помощью которого сымитировано функционирование страховой компании. Была проведена серия расчетов комбинированного показателя при различных комбинациях весовых коэффициентов. В таблице 2 представлены результаты расчетов.

Таблица 2

Результаты расчетов комбинированного показателя (КП)

	Весовые коэффициенты				Характеристики договора перестрахования				КП
№	VaR	CVaR	ВР	Пр	α'	α''	d'	d''
1	25	25	25	25	0,6	0	16000	26000	-0,6
2	0	33	33	33	1	0	0	30000	-0,4
3	33	0	33	33	1	0	6000	34000	-0,47
4	33	33	0	33	0,6	0	16000	26000	-0,8
5	33	33	33	0	0,2	0	10000	30000	-0,89
6	40	20	20	20	0,6	0	16000	26000	-0,74
7	20	40	20	20	0,4	0	16000	24000	-0,72
8	20	20	40	20	0,6	0	16000	26000	-0,48
9	20	20	20	40	1	0	6000	34000	-0,52

5. Заключение

В работе определен комбинированный договор перестрахования, экспериментально исследована эффективность его применения для страховой компании при учете ряда как эндогенных, так и экзогенных факторов. Установлено, что в большинстве случаев применение комбинированного договора эффективнее пропорционального и эксцедентного.

Литература:

1. Шахов В.В., Страхование: Учебник для вузов. — М.: ЮНИТИ, 2003. - 311 с.

2. В.Д. Ногин. Принятие решений при многих критериях: Учебно-методическое пособие.– СПб.: Издательство «ЮТАС», 2007. – 104с.

3. Орлов А.И., Математика случая. Вероятность и статистика – основные факты: Учебное пособие. – М.: Издательство«МЗ-Пресс», 2004. – 110с.

4. Гвозденко А. А., Страхование: Учебное пособие. — М.: Издательство «Проспект», 2006. - 464 с.

5. Борисов Б.И., Динамический метод анализа и управления деятельностью страховой компании: Автореферат диссертации.- М., 2007. –24 с.