Ванчин Е.А., Куликовский К.Л.

Самарский государственный технический университет, Россия

Определение смещения геометрического центра ППЗ относительно оси МНГП в процессе поиска его местоположения.

Для транспортировки нефти и газа на большие расстояния используются магистральные нефтегазопроводы (МНГП), часть из которых располагается на дне океанов и морей в глубинах достигающих 200 метров. При этом с целью соблюдения экологической безопасности необходима постоянная инспекция состояния МНГП. Для проведения инспекции целесообразно использовать подводные планирующие зонды (ППЗ) [1].

ППЗ путем изменения своей плавучести и положения центра тяжести перемещается на большие расстояния, не всплывая на поверхность, при минимальных затратах энергии. Планирующий зонд является носителем аппаратуры для получения необходимой информации.

Для проведения инспекции важной задачей является поиск нефтегазопровода под водой и определение угла пересечения траектории движения ППЗ с осью МНГП. Это необходимо для ориентации зонда таким образом, что бы траектория его движения совпала с осью МНГП и с требуемым направлением.

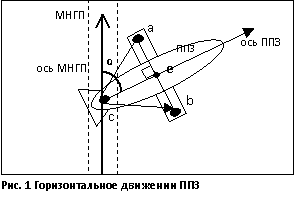
Эта задача решается при помощи информационно измерительной системы (ИИС), которая основана на применении электромагнитного метода измерения. ИИС позволяет определить момент встречи с нефтепроводом и угол α, под которым пересекается траектория движения зонда с осью нефтепровода (рис.1). Указанная система описана в [2].

В состав ИИС входит три электромагнитных преобразователя (ЭП). При этом ЭП_a и ЭП_b, расположены на крыльях зонда на оси a-b в точках a и b симметрично относительно оси планирующего зонда, а ЭП_с расположен в хвостовой части аппарата в точке с. Каждый из преобразователей попеременно выступает в роли источника электромагнитных импульсов и приемника отраженного от МНГП сигнала[3]. При этом определяется момент поступления отраженного сигнала от нефтепровода на преобразователи ЭП_a или ЭП_b и рассчитывается по приведенному алгоритму в [2] угол α.

Приведенный алгоритм предусматривает движение зонда только в горизонтальной плоскости – параллельно дну. При этом появление отраженного сигнала, на одном из преобразователей, соответствует положению ППЗ над нефтегазопроводом, т.к. сигналы от ЭП излучаются перпендикулярно донной поверхности водной среды. Это является частным случаем движения ППЗ.

Однако ППЗ перемещается по траектории подобной синусоиде, всплывая и погружаясь над поверхностью дна. Поэтому в момент времени появления отраженного сигнала на одном из преобразователей ЭП_a или ЭП_b, геометрический центр тяжести зонда может находиться на некотором расстоянии от МНГП. Для внесения коррекции в алгоритм управления, необходимо знать на каком расстоянии находится указанный геометрический центр от оси нефтепровода, а также угол α и скорость движения ППЗ.

Далее рассматриваются вопросы определения величины смещения геометрического центра тяжести ППЗ, в момент появления отраженных сигналов в зависимости от высоты его положения к углу дифферента.

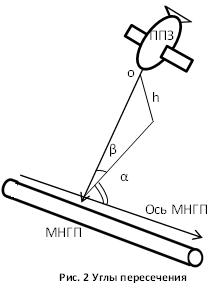
На рисунке 2 изображено движения планирующего зонд в пространстве под углом α к оси МНГП в горизонтальной плоскости и под углом β в вертикальной плоскости.

Для нахождения величины смещения необходимо определить угол α и скорость движения зонда. На рисунке 3 изображено положение ППЗ в процессе его погружения. Аналогично происходит всплытие аппарата. В момент нахождения аппарата в точке p возникает первый сигнал на преобразователе a или b и начинается отсчет . Через этот промежуток времени сигнал возникает на втором датчике, если движение зонда осуществляется под углом α≠90⁰. Если сигнал возникнет одновременно на a и b, значит ППЗ движется под углом α=90⁰. В точке d возникает отраженный сигнал на преобразователе в точке c. После этого момента можем определить скорость движения, при помощи соотношения:

,

где это расстояние между точкой e в хвосте зонда и серединой оси a-b (рис.2).

Согласно рисунку 3 пройденное зондом расстояние за промежуток времени равно l=l_{dp .} Так как зонд движется под углом β, то для расчёта скорости необходимо использовать проекцию l_dp т.е. расстояние l_dn. Это расстояние можем определить, используя выражение:

Угол β найдем с помощью выражения:

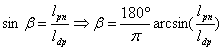
Т.е. выражение для l_dn примет вид:

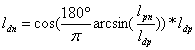
Соответственно выражение для определения скорости движения зонда:

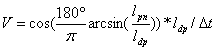(1)

Используя ранее полученные выражения из [2] рассчитаем угол α:

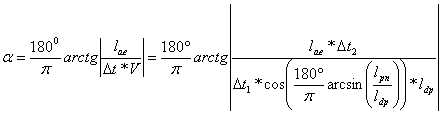(2)

Где время поступления сигналов между датчиками a и b, время поступления на датчик в точке с.

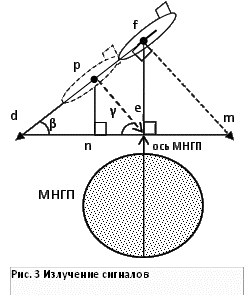
На рисунке 3 изображено движение зонда над МНГП в вертикальной плоскости. Зонд двигается на разных высотах от нефтепровода. И при больших углах наклона, излученные электромагнитные сигналы отразятся после прохождения зондом некоторого расстояние от МНГП. В момент нахождения аппарата в точке f , излучение сигналов будет попадать в точку m. Т.е. фактически зонд будет находиться над МНГП, но отраженный сигнал не поступит. В момент нахождения в точке p, отраженный сигнал зафиксируется на преобразователях. При этом зонд будет находиться на расстоянии l_ne от оси МНГП. Расстояние l_ne это искомое значение смещения.

Значение l_pn можно определить при помощи датчика давления. Как функция от времени:

Определим длину l_ne , используя соотношение:

(3)

Где γ :

Таким образом, по выражению (2) определим угол α. При этом по выражению (3) можно всегда знать положение зонда в момент измерения и ввести соответствующую коррекцию в алгоритм его управления.

Литература.

1. Ванчин Е.А., Куликовский К.Л. Информационно измерительная и управляющая система для поиска утечек в магистральных нефтепроводах и формирования траектории движения планирующего зонда//Восточное партнерство. 2013 Том 30.

2. Ванчин Е.А., Куликовский К.Л. Анализ факторов, влияющих на погрешности измерения угла пересечения планирующего зонда с нефтепроводом// Перспективные вопросы мировой науки. 2013 Том 37.

3. Куликовский К.Л., Ванчин Е.А. Способы построения информационно измерительных систем для подводных планирующих зондов// Современный научный вестник. 2012 №14.

4. Куликовский К.Л., Ванчин Е.А. Определение положения планирующего зонда с помощью измерительной аппаратуры на базе магнитометров//Новости передовой науки. 2013 Том 55.