Современные информационные

технологии/ 4 Информационная

безопастность

Ismagul R.

Kostanai State University named after A. Baitursynov, Kazakhstan

Аlmost multiperiodic solution of evolyutsion equations

 Let’s introduce some notations and definitions:  -the class of n-dimensional -functions, -satisfying the сonditions.

and almost multiperiodic in с - vector- almost period , where when ; countable-dimensional vector, where; W_m и V_m - functionals that assign vectors W_m= ( φ₁, …, φ_т, 0,…) и V_m= ( 0,…,0, φ_m+1,φ_т+2, …) to the vector φ = (φ1, ..., φt, ...).

Let’s consider a system of integrodifferential equations of the form 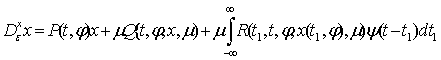, (1)  where x, Q, R are n-vectors-columns; P (t, φ) is a matrix of dimension n × n, φ = (φ1, ..., φt, ...) is a countable vector, and ,>0 are small parameters.
Let’s consider that the conditions [1,c.168] и () are met if:
1) vector-function is bounded and contiguous with all
variables, and has limited contiguous derivatives of first order in ,; diagonally - almost in period, belongs to -class evenly relatively to;

2) continuous function provides improper integral, where is permanent.

Let’s contemplate the differential operator:

.

To reduce the record we’ll take . It should be noted that the coefficients of Lipshitce enhanced condition for vector-function are .

Let’s contemplate the linearized equation:

. (2)

Let be the characteristic function of the functional, which satisfies the integral equation

.
 .
For characteristic function there are rates analogous to relations of the form I(a-b) и 1⁰-9⁰.

Let’s consider the functional Т, representing each vector-function in vector-function

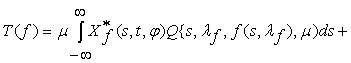
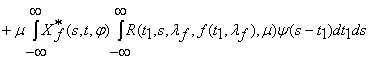
, where

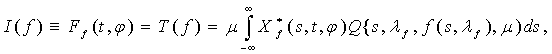
which is known from [1].

We will study

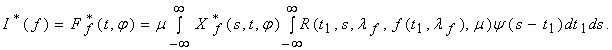
Considering that , we can write .

From rates III(a-d) we can conclude that there is such a number , for which with all there are the following relations:

1) ,

2) ,

3) ,

4) .

Thus, we come to the statement of theorem 1.

Theorem 1. If the conditions , are met for the equation (1), than for all the meanings, equation (1) has a single almost multiperiodic solution from the class , converging in a zero vector with .

REFERENCES:

1. Umbetzhanov D.U. Almost periodic solutions of evolution equations. Alma-Ata, Nauka, 1990, 188 p.