Д.т.н. Туленбаев М.С., к.т.н. Беглерова С.Т.,

Жульева Л.В., Маковецкая А.А.

Таразский государственный университет им. М.Х.Дулати, Казахстан

Синтез квазивейвлетов для информационных систем обработки экоаналитических данных

Введение. Основой информационных систем экологического мониторинга являются первичные источники информации о состоянии окружающей среды. Последнее десятилетие характеризуется устойчивой тенденцией к широкому распространению химико-аналитических информационных систем (ХАИС) с универсальными физико-химическими анализаторами состава и свойств вещества, особенно анализаторами спектрального типа (хроматографами, спектрометрами излучения, масс-спектрометрами и др.). Названные аналитические приборы нашли применение для решения задач экологической направленности в составе химико-аналитических комплексов (ХАК) типа ИНЛАН (РФ), Agilent Technologies (USA) и Perkin Elmer. Приборы этих фирм внесены в реестр государственной системы обеспечения единства измерений РК №KZ.02.02.00192-2003. Основным фактором, затрудняющим использование аналитических приборов (АП), является сложность и разнообразие алгоритмов первичной обработки выходных сигналов. К задачам первичной обработки относятся: дискретное представление сигнала АП, предварительная фильтрация (сглаживание), обнаружение информативного (полезного) участка сигнала, коррекция дрейфа и оценка параметров полезного сигнала [1].

Кратно-масштабный анализ сигналов АП. Исследования в области теории обобщенного спектрального анализа позволили не только по-новому оценить значение классического спектрального анализа Фурье и пределы его практического применения, но и создали методы и критерии синтеза базисных систем наиболее приспособленных для решения конкретной практической задачи. Примером тому является активно развивающаяся с середины 80-х годов теория вейвлетов. Благодаря прозрачности физической интерпретации результатов анализа, очень сходной с "частотным" подходом в Фурье-анализе, вейвлет технология стала популярным и эффективным средством анализа нестационарных сигналов в акустике, сейсмике, экологии и др. областях. Выходные сигналы аналитических приборов (АП) химико-аналитических комплексов (ХАК) экологических информационных систем в связи с различием физической сущности самих приборов, а также условии проведения анализа относятся к нестационарным сигналам с искажающими составляющими - шумами, помехами, дрейфом и т.п. [1,2,3]

Вейвлет технологии являются новым инструментом в обработке сигналов и изображений путем их разложения по адаптивной системе базисных функций и последующего анализа спектральных компонентов с целью выделения значимой информации на фоне помех. Сам термин "вейвлет" использовался ранее в литературе, но свое текущее понятие он получил в статье J. Morlet и A. Grossman (1984г.), посвященной исследованиям сейсмических сигналов с помощью базиса, который и назвали вейвлетом. Эта работа дала начало развитию теории вейвлетов в последующие годы целым рядом авторов: зарубежных S. Mallat, L.K. Meyer, D.J. Lemarie, I. Daubechies, A. Cohen, R.R. Chui и др. [5,6] и российских авторов [4,7]. Математическая формализация, данная работами Mallat и Meyer, привела к созданию теоретических основ вейвлет-анализа, названного мультиразрешающим (кратно-масштабным) анализом (КМА).

Проектирование квазивейвлетов для систем обработки экоаналитических данных. Суть проектирования квазивейвлетов есть определение коэффициентов h(n) и  масштабирующего уравнения. Эти коэффициенты полностью определяют масштабирующую и вейвлетную функции и используются в качестве импульсных откликов банков цифровых фильтров вейвлет-анализа сигналов. В отличие от вейвлетов Добеши коэффициенты h(n) квазивейвлетов должны вычисляться из заданной (или выбранной из некоторых соображений) функции u(t) – "кандидата" в масштабирующие функции. Алгоритм проектирования вейвлет-подобного базиса (квазивейвлета) включает несколько этапов[3,7].

Этап нормирования. Выбираем в качестве u(t) приборную функцию АП

                                              (1)

Проектируем систему линейно-независимых функций. Для этого путем смещения u(t) с шагом b образуем множество функций

,

где ; – среднеквадратическая ширина или ширина на половине высоты (полуширина) пика. Чтобы минимизировать ошибку вычислений, функцию u(t) задают  дискретными отсчетами на ширине m. Выберем норму сдвига (относительный шаг) b0 такой, чтобы функции  образовывали базис Рисса [4].

Ортогонализация. Воспользовавшись модифицированным способом ортогонализации Грамма-Шмидта, предложенным в [1,4], образуем из системы функций {uk(t)} функцию j(t), сдвиги которой с шагом b0 формируют ортонормированный базис , и путем ее сжатия вдвое – базис .

Определение коэффициентов масштабирующего уравнения. Для вычисления h воспользуемся формулой:

                      (2).

Ограничение числа коэффициентов h и вычисление g. Вследствие того, что функция u(t) обычно задана на всей числовой оси, но достаточно быстро убывает, поэтому коэффициенты h также быстро убывают. С учетом этого обстоятельства для построения блоков фильтров с конечной импульсной характеристикой число этих коэффициентов можно ограничить, отбросив коэффициенты, например,  для |n| больше некоторого N. Заметим, что число оставшихся коэффициентов должно быть четным. Коэффициенты g(n) вычисляются по формуле:

                     (3)

Проверка решения. Производится подстановкой в масштабирующее уравнение полученных коэффициентов h, функции  и вычисление ошибки по формуле:

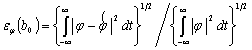                        (4).

Проектирование биортогональных квазивейвлетов начинается с выбора (задания) функций:

,                                                             (5)

                                              (6).

Сдвиги таких функций с шагом b0 образуют биортогональную смещенную базисную систему (СБС), для выбранного шага сдвига эти функции должны удовлетворять масштабирующим уравнениям:

,                                      (7)

.                                     (8)

Проектирование, также как и в ортонормированном случае, состоит из нескольких этапов.

Нормировка. Полагаем, что

.                                            (9)

Проектирование линейно-независимой системы функции. Путем смещения u(t) с шагом b образуем множество функций , где ; a– среднеквадратическая ширина или ширина на половине высоты (полуширина) пика.

Ортогонализация. Используя модифицированную процедуру ортогонализации Грамма-Шмидта, предложенным в [1], образуем из системы функций  функции j(t) и , сдвиги которых с шагом b0 формируют биортогональный базис , а путем сжатия вдвое – базис  и .

Определение коэффициентов масштабирующего уравнения. Для вычисления h воспользуемся формулами (6)

Ограничение числа коэффициентов h,  и вычисление g, . Число этих коэффициентов, так же как и в ортонормированном случае, можно ограничить, отбросив коэффициенты, например,  при |n| больше некоторого N. Заметим, что число оставшихся коэффициентов должно быть четным. Коэффициенты  вычисляются по формулам:

,                                               (10)

.                                              (11)

Проверка решения. Подставим в масштабирующие уравнения:

                                           (12)

,                                          (13)

полученные коэффициенты h, вычислим функцию  и определим ошибку по формуле (4), которая характеризует точность выполнения равенства (12) в зависимости от шага b0. Выполняя процедуру ортогонализации и вычисление h при различных величинах b0 можно построить функцию e(b0) и найти ее минимум. Аналогичные операции необходимо выполнить для проверки соответствия функции  масштабирующему уравнению (13). Как показывают расчеты, вид функции e(b0)  для различных функций u(t) отличается мало, поэтому интервал значений b0, при которых функции  удовлетворяют соответствующим масштабирующим уравнениям, будет равным . Полученные приведенным выше способом коэффициенты  и  должны удовлетворять обязательным соотношениям, налагаемым на них теорией КМА.

Выводы. При обработке реальных сигналов приборов, аппаратная функция известна, как правило, с некоторым приближением. В этом случае необходимо аппроксимировать функцией H(t) одиночный пик наблюдаемого сигнала, задать шаг b0 (шаг ) и вычислить коэффициенты y, h и g. В процессе отладки программного обеспечения на градуировочных объектах, варьируя коэффициентом b и шагом b "настраивают" систему обработки под особенности реального прибора. В результате обработки экоаналитических данных подавляется шум (в несколько раз) и улучшаются оценки значимых параметров обработки.

Литература:

1.                      Туленбаев М.С. Синтез адаптивных базисов спектрального представления сигналов химико-аналитических комплексов // Природопользование и проблемы антропосферы: Вестн. ТарГУ им. М.Х. Дулати. – Тараз, 2009. – №3. – С. 189-196.

2.                      Туленбаев М.С. Спектральные агоритмы обработки сигналов химико-аналитических комплексов в геоинформационных системах экомониторинга. // Вестник НАН РК, Алматы, 2010. №1, с.11-17.

3.                      Туленбаев М.С. Вейвлет-подобные базисы ортогонального разложения сигналов в информационных системах экологического мониторинга // VI Дулатовские чтения: матер.Междунар. науч.-практ. конф. – Тараз, 2009. – Ч. III. – С. 51-54.

4.                      Новиков Л.В. Модифицированные вейвлеты в обработке данных аналитических приборов // Научное приборостроение. 2006. – Т.16, №1, С. 3-14.

5.                      Daubechies I. Ten Lectures on Wavelets. SIAM press. Philadelphia, 1992. (Перевод: Добеши И. Десять лекций по вейвлетам. Москва-Ижевск: РИЦ РХД, 2001).

6.                      Mallat S. A wavelet Tour of Signal Processing. San Diego: Academic Press, 1999. (Перевод: Маллат С. Вейвлеты в обработке сигналов. М.: Мир, 2005).

7.                      Новиков Л.В. Обработка сигналов на основе ортонормированных квазивейвлетов // Приборостроение: Изв. Вузов. – 2007. – Т.50, №1. – С. 3-10.