Математика/5. Математическое моделирование

      к.ф.-м.н. доц. В.И. Евсеев  

Казанский  (Приволжский) федеральный университет, Казань, Россия,

                          кафедра прикладной информатики

   УДК 681.32                        1 - vladislaw.evseev@yandex.ru, т.89047610772

 

      МАТРИЧНЫЙ АНАЛИЗ БИНАРНЫХ ОПЕРАЦИЙ

 

      § 1 Понятие о бинарных операциях

 

         Построение сложных высказываний связано с принципами соединения простых высказываний по определенным схемам с помощью бинарных логических операций.           Пусть заданы два простых высказывания

 

                                             (1.1)

Здесь мы указываем в скобках значения функции истинности каждого высказывания:

 

                                                                       (1.2)

 

Бинарная операция связывает эти простые высказывания в сложное высказывание, соответствующее  по смыслу сложно-сочинённому или сложно-подчинённому предложению с некоторыми союзами. Сами соединительные союзы в математической логике имеют символические обозначения, а результаты бинарных операций по логическому значению однозначно определяются значениями исходных высказываний по законам, отражающим суть самой операции.

         Мы будем придерживаться методики и терминологии, в которой все бинарные операции условно подразделяются на основные и взаимные. Взаимные операции представляют  собой внешние отрицания основных операций. Заметим, что в процессе построения сложных высказываний должен сохраняться смысл самих исходных высказываний, а полученное сложное высказывание не должно быть бессмыслицей.

         Любая бинарная операция представляет собой «логическое произведение» двух элементов из различных универсумов высказываний (в частности, из одного, дважды взятого универсума W): если обозначить саму бинарную операцию символом «», а «логический квадрат» самого универсума высказываний – символом «», то можно записать:

                                       (1.3)

Сама бинарная операция рассматривается как отображение . Реальное выражение этого отображения определяется структурными формулами вида (5.8), в которых указываются как основная бинарная операция, так и её внешнее отрицание.

         Основными бинарными операциями являются:

а) логическое умножение или конъюнкция, которая обозначается символом  «&»  (или символом ); этот символ читается как союз «и»:

 

                                                                     (1.4)

б) логическое сложение или дизъюнкция, которая обозначается символом   и  читается как союз «или»:

 

                                                                                                (1.5)

в) логическое следование или импликация, которая обозначается символом  «» и читается «если…, то…»:

 

                                                                                                       (1.6)

 

г) логическое тождество или эквиваленция, которая обозначается символом «» и читается «…тогда и только тогда, когда…»:

 

                                                                                             (1.7)

 

Кроме того, существует четыре бинарных операции,  взаимных к основным; они будут рассмотрены в дальнейшем. Если обозначить классы истинности как , то бинарную операцию можно представить как результат логического умножения классов истинности. Например,

 

&  =  ,    & = ,  &   =  .                           (1.8)

 

В общем случае результирующая матрица имеет вид:

 

 

k

          0

          1

       j

i

   0 

   1

   0

   1

0

 

1

 

 

 

 

 

 

 

 

 

 

 

Величины   принимают значения {0,1} и могут быть представлены таблицей структуры бинарной операции:

          Матричная запись оказывается более удобной для многих случаев сложных высказываний, поэтому мы будем отдавать ей предпочтение. Такая таблица называется арифметической, потому что определяет значения арифметической функции истинности бинарной операции по значениям функций исходных высказываний. Её аналогом для записи структуры бинарной операции через выражения самих заданных высказываний и их отрицаний является «символьный массив» бинарной операции, который в общем случае имеет вид (стрелка указывает порядок вхождения аргументов в формулу):

                                  

      Y        

X

  

 

 

         

 

 

 

        

 Эта схема называется «метод четырёх блоков», так как на соответствующих пересечениях исходных элементов и их отрицаний стоят блоки, отражающие их конъюнкции. В каждой бинарной операции существует собственный набор рабочих блоков, соответствующий наборам единичных значений в арифметическом массиве. Следовательно, сам арифметический массив для произвольной бинарной операции может быть записан в виде таблицы:

 

                                     

      Y        

X

   0

  1

 0

         

 

 1

    

 

 

 

Здесь:   –  значения функции истинности изучаемой бинарной операции, они принадлежат множеству {0,1}. Совокупность рабочих блоков бинарной операции в общем случае следует из формулы:

 

                                                  (1.9)

 

Эта формула характеризует «логическое произведение» матриц  истинности и символьного массива. Оно выполняется поэлементно с последующим суммированием результатов. Аналогично находится выражение для отрицания бинарной операции общего вида:

 

        

        (1.10)

 

Формулы (1.9) и (1.10) позволяют структурировать выражение для :

k

          0

          1

       j

i

   0 

   1

   0

   1

0

 

 

 

1

 

 

                           

 

 

 

 

 

        

        

 

 Вычисляем теперь значение функции истинности для общего вида бинарной операции:

 

                   (1.11)

 

Для каждой бинарной операции указывается определяющее характеристическое свойство, таблица истинности (двух видов), структура рабочих блоков и функция истинности.

 

                   § 2. Конъюнкция высказываний.

 

         По своему определяющему свойству конъюнкция является истиной только в том случае, когда оба исходных высказывания – истины; в остальных случаях результат является ложью. Согласно этому свойству можно построить таблицу истинности данного сложного высказывания. Различают два вида таких таблиц:

          –  линейная таблица, в которой содержится три строки, отражающих  возможные сочетания значений истинности исходных суждений и результата:                                                                                (2.1)   

 

   X

    0

    0 

    1

    1

   Y

    0

    1

     0

    1

   Z

    0

   0

    0

    1

 

          –  матричная таблица, в которой результирующие значения образуют квадратную матрицу второго порядка:

 

                                              

                           

      Y        

X

   0

  1

 0

   0     

  0

 1

   0

  1

        

Как было указано ранее, стрелкой в верхнем левом углу обозначается порядок вхождения простых высказываний в рассматриваемое сложное высказывание. Существуют симметричные и несимметричные бинарные операции. Для симметричных бинарных операций изображение стрелки не обязательно, а для несимметричных – существенно. Поэтому мы в случае несимметричных операций обязательно будем указывать стрелкой их порядок.

В более сложных логических операциях стрелка не указывается, но предполагается определённая последовательность действий (в большинстве случаев сложных логических операций применяется лексикографический или заранее оговорённый порядок вхождения аргументов). Если полученные результаты применить к конъюнкции, то получаем:       её единственный рабочий блок расположен в соответствии с тем, что = 1, а остальные параметры равны нулю, то есть, символьный массив имеет вид:

                           

      Y        

X

  

 

 

         

 

 

 

        

Значит, функция истинности конъюнкции имеет вид:

 

                                                                     (2.2)

 

Конъюнкция является основной составляющей для всех основных операций.

В некоторых случаях (особенно для сложных логических операций) символ конъюнкции не используется, и она записывается как алгебраическое произведение сомножителей –  высказываний.

         Для конъюнкции матрица логической структуры имеет вид:

 

 

                  

k

          0

          1

       j

i

   0 

   1

   0

   1

0

 

 0

 0

1

 

1

0

0

 1

        

 

 

 

 

 

 

        

                   § 3. Дизъюнкция высказываний             

 

           Логическое сложение или дизъюнкция  обозначается символом «», который читается как «или» (заметим, что по смыслу это – соединительный союз, потому что допускается совместная истинность исходных высказываний). По своему характеристическому свойству дизъюнкция является ложью только в том случае, когда оба исходных высказывания – ложные. В остальных случаях результат является истиной. Вид операции:

 

                                               .                                       (3.1)

 

         Из  основного свойства следует вид арифметического массива дизъюнкции 

 

      Y        

X

   0

  1

 0

   0     

  1

 1

   1

  1

                  

 

 

 

 

 

 

Теперь можно записать символьный массив дизъюнкции через рабочие блоки:

 

                                                            ( 3.2)

        

При этом матрица символьного массива дизъюнкции имеет вид:

 

      Y        

X

  

 

 

         

 

 

 

                                     


 Получаем формулу для функции истинности дизъюнкции:

 

                                (3.3)

 

         В этой формуле можно провести преобразование с учетом выражения функции истинности отрицания высказываний:

 

                                                               (3.4)

 

         Подставляя эти значения в выражение (7.3), получим:

 

                  

k

          0

          1

       j

i

   0 

   1

   0

   1

0

 

 

 0

  0

 1

1

 

 0

 0

1

 1

 

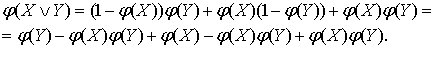
         Следовательно, получаем новый вид для функции истинности дизъюнкции:

 

                                                         (3.5)

 

         Обе рассмотренные ранее бинарные операции – конъюнкция и дизъюнкция – были симметричными операциями (их рабочие блоки располагаются симметрично относительно главной диагонали матрицы символьного массива). Теперь  построим матрицу логической структуры дизъюнкции.

 

                   § 4. Импликация высказываний

 

          Из основных бинарных операций только одна оказывается несимметричной. Эта операция соответствует построению сложно подчинённого  предложения по структуре «если X, то Y». Здесь первое высказывание Х называется причиной или посылкой, а второе Y – следствием. Такая операция называется логическим следованием или импликацией, она обозначается:

 

                   .                                                               (4.1)

 

 По своему характеристическому свойству импликация является ложью лишь в том случае, когда посылка – истина, а следствие  –  ложь.  Из этого свойства получаем  вид арифметической матричной таблицы истинности:

 

                           

      Y        

X

      

 

 

    1    

   1

 

 0

   1 

                           

 

 

 

 

 

        

 

В дальнейшем мы будем применять только матричную запись таблицы истинности бинарных операций.   

Из таблицы  следует вид символьного массива импликации

                                              

                                              

 

                                     

      Y        

X

  

 

 

         

 

 

 

                           

 

 

 

 

 

                           

 

Следовательно, явная запись совокупности рабочих блоков такова:

 

                                                   (4.2)

 

Теперь получаем формулу для функции истинности импликации:

                  

                              (4.3)

 

         Укажем также матрицу логической структуры импликации.

Она имеет следующий вид:

 

                  

                    

 

                  

k

          0

          1

       j

i

   0 

   1

   0

   1

0

 

 0

 0

  1

 1

1

 

 1

 0

0

 1

 

                  

                           

 

 

 

        

 

 

 

 

                            § 5. Эквиваленция высказываний

 

  Следующей основной бинарной операцией является часто применяемое логическое тождество или эквиваленция. Два высказывания называются эквивалентными, если у них совпадают логические значения, то есть, либо они оба одновременно  –  ложные, либо оба одновременно – истинные. По своему основному характеристическому свойству эквиваленция является истиной только в том случае, когда исходные высказывания логически эквивалентны, а в двух других случаях эта операция дает в результате ложь. Эквиваленция обозначается символически:

 

                                                .                                    (5.1)

        

По этому свойству получаем арифметическую матричную таблицу истинности для эквиваленции:

                           

      Y        

X

  

 

 

    1    

   0

 

 0

   1 

                           

 

 

 

 

 

        

Отсюда находим символьный массив для эквиваленции, в котором всего два рабочих блока:        

      Y        

X

  

 

 

         

 

 

 

                                     

 

 

 

 

 

 

 

По рабочим блокам записываем формулу для символьного массива эквиваленции:

                                                                         (5.2)

 

         Теперь получаем формулу для функции истинности:

 

                                                         (5.3)

 

         Если применить формулы отрицания высказываний и преобразовать с их помощью выражение (9.3), то можно придти к формуле:

 

                                                                (5.4).

 

         Рекомендуем читателям получать эту формулу самостоятельно.

Теперь построим матрицу структуры эквиваленции:

 

k

          0

          1

       j

i

   0 

   1

   0

   1

0

 

 0

 1

  1

 0

1

 

 1

 0

0

 1

 

 

 

 

                  

                    

 

                  

 

         § 6. Композиция отрицания с основными

                            бинарными операциями

 

         Если задана некоторая бинарная операция

 

                            ,

 

то для неё возможны  четыре различных способа построения композиции с применением отрицания:

а) внутреннее отрицание только первого аргумента

 

                     ,                                                                 (6.1)

б) внутреннее отрицание только второго аргумента

                   ,                                                                           (6.2)

в) внутренне отрицание обоих аргументов

 

                    ,                                                                 (6.3)

г) внешнее отрицание всей бинарной операции

                           

         .                                                                         (6.4)

 

        

Рассмотрим строение этих композиций.

а) Исходная бинарная операция имеет арифметический массив

 

                           

      Y        

X

   0

  1

 0

         

 

 1

    

 


         Внутреннее отрицание элемента Х имеет вид таблицы:

 

                                           

                           

X

0

1

1

0

                           

 

 

 

 Значит, в данной  операции первая строка арифметического массива будет соответствовать значению «1», а вторая строка – значению «0».

Таким образом, строки исходного арифметического массива меняются

 местами:

                                              

                                      ,

                  

                                              

      Y        

X

   0

  1

 0

         

 

 1

    

 

 

         При этом получаем формулу для матрицы истинности данной бинарной операции:

 

           (6.5)

 

б) Во втором случае по аналогии получаем, что при отрицании по второму аргументу будут меняться местами  столбцы арифметического массива.

         При

                                   

приходим к арифметическому массиву этой композиции, который имеет вид:

                                              

 

                           

      Y        

X

   0

  1

 0

         

 

 1

    

 

        

Функция истинности записывается аналогично предыдущему случаю (рекомендуется для самостоятельного вычисления).

в) Когда рассматривается внутреннее отрицание обоих аргументов, следует представлять эту операцию как последовательную композицию первого и второго видов отрицаний. Поэтому, к формуле для применяется отрицание по второму аргументу, то есть, у матрицы её массива переставляются столбцы, и в результате получаем таблицу:

                                     

                                     

        

                           

      Y        

X

   0

  1

 0

         

 

 1

    

 

 

Рекомендуем читателям самостоятельно записать значение функции истинности для этой композиции.      

г) Для случая внешнего отрицания мы получаем, что

 

                                      ,

что фактически означает:      

         Следовательно, арифметический массив этой операции получается заменой исходных значений параметров на взаимно противоположные

значения:

 

                           

      Y        

X

   0

  1

 0

     

 1

        

 

         § 17. Частные случаи композиций бинарных                                операций с отрицанием

 

          а) Композиция конъюнкции с отрицанием.

         Исходная операция конъюнкции характеризуется арифметическим массивом:              

                           

      Y        

X

   0

  1

 0

         

 

 1

    

 

 

Для неё функция истинности имеет вид

 

                           

 

Согласно построенной общей теории при отрицании первого аргумента в операции конъюнкции происходит перестановка первой и второй строк арифметического массива, что приводит к таблице

                                              

                                     

        

      Y        

X

   0

  1

 0

         

  1

 1

    

  0

        

 

                                     

 

 

 

 

Значит, функция истинности данной операции имеет вид

                                                                   (7.1)

         Аналогично, при отрицании по второму аргументу получается матрица арифметического массива для операции         

                  

      Y        

X

   0

  1

 0

         

  0

 1

    1

  0

                  

 

 

                                                       

 

 

В этом случае функция истинности принимает вид

                           

                                                                         (7.2)

         При внутреннем отрицании по обоим аргументам для операции вида

                                     

получаем арифметический массив:

        

      Y        

X

   0

  1

 0

   1     

  0

 1

    0

  0

 

                  

 

 

 

 

и функцию истинности

 

                                                            (7.3)

Внешнее отрицание конъюнкции приводит к операции

 

                           

Матрица истинности этой операции имеет вид

 

                           

      Y        

X

   0

  1

 0

   1     

  1

 1

    1

  0

 

                  

 

 

 

 

В технических приложениях эта операция носит наименование «штрих Шеффера», а по методике И.Канта «штокъюнкции» и обозначается

 

                                                                                 (7.4)

Для штокъюнкции получаем формулу совокупности рабочих блоков

 

                           

  Функцию истинности штокъюнкции  мы сразу запишем в виде, согласованном с таблицей логической структуры конъюнкции

 

                                                                  (7.5)

 

         б) Композиция дизъюнкции с отрицанием.

 

         Дизъюнкция (или логическое сложение) имеет арифметический массив:                                                    

      Y        

X

   0

  1

 0

   0     

  1

 1

    1

  1

 

 

 

 

 

 

 

Её функция истинности характеризуется формулой (5.10).

При отрицании по первому аргументу получаем таблицу

                                     

      Y        

X

   0

  1

 0

   1     

  1

 1

    0

  1

 

 

 

 

 

 

 

и соответствующую формулу для функции истинности:

 

                                (7.6 )

 

Эту формулу можно преобразовать с учетом выражений для функции истинности отрицания, тогда получим:

 

        

                                                                 (7.7 )

 

Сравнивая полученный результат с формулой (5.13), приходим к выводу, что имеет место равенство:

 

                                                                               (7.8)

 

         Этой формулой начинается получение многочисленных взаимосвязей между различными бинарными операциями.     Все они соответствуют   формулам, с помощью которых можно представить один и тот же блок в структуре четырех блоков, которые определённы для каждой из рассматриваемых операций и их композиций. Рассмотрим случай отрицания дизъюнкции по второму аргументу. В этом случае получаем арифметический массив                                   

                                     

                           

      Y        

X

   0

  1

 0

   1     

  0

 1

    1

  1

 

 

 

 

 

 

 

Здесь функция истинности принимает вид

 

                                                                 (7.9)

 

Для неё получаем связь с операций импликации в виде

 

                                                                               (7.10)

 

Для внутреннего отрицания дизъюнкции по обоим аргументам, находим

 

                                                                  

        

      Y        

X

   0

  1

 0

   1     

  1

 1

    1

  0

        

                           

 

 

 

 

 

        

Здесь рабочие блоки образуют конструкт

                  

                                                            (7.11)                                    

Следовательно, в этом случае функция истинности имеет вид

 

                   .                 (11.12)

 

Учитывая вид арифметического массива, можно записать эту формулу в другом виде:

                  

                   .                                             ( 7.13)

 

Отсюда следует формула взаимосвязи данной операции с внешним отрицанием конъюнкции:

 

                   .                                                            ( 7.14)

 

Эта формула отражает вид1-го закона до Моргана.

         Кроме того, рассмотренная операция  совпадает с рассмотренной выше операцией     «штокъюнкция» 

 

                            .                           (7.15)

 

 

    Теперь перейдём к рассмотрению внешнего отрицания дизъюнкции

                                     

                                      .

        

         Для этой композиции находим арифметический массив:

                  

      Y        

X

   0

  1

 0

   1     

  0

 1

    0

  0

 

 

 

                  

 

 

 

 

Значит, единственный рабочий блок этой операции

 

                            ,

а ее функция истинности

 

                                                                          (7.16)

 

         Эта операция также имеет своё наименование и обозначение. По методике И.Канта она называется «нильюнкция» и обозначается:

 

                                                                                     ( 7.17)

 

(Она читается «Х» ниль «У»). Кроме того, в технических приложениях она имеет наименование «стрелка Пирса», в честь одного из математиков, изучавших ее и нашедших ей многочисленные технические приложения.

Мы будем следовать традициям И.Канта.

         Операция нильюнкции, как видно из строения ее рабочих блоков, оказывается взаимной к операции дизъюнкции, так как

 

                            .                                                   ( 7.18).

 

         Эта формула носит наименование второго закона де Моргана.

  читателям.

 

в) Композиция импликации с отрицанием.

        

         Из основных операций только импликация исходно является

несимметричной логической операцией. При её  отрицаниях результат может быть как симметричной, так и несимметричной функцией. Рабочие блоки импликации определяются формулой (5.12). Для этой операции матричная таблица истинности имеет следующий вид

 

                                 

                                     

      Y        

X

   0

  1

 0

   1     

  1

 1

    0

  1

 

 

 

                  

 

 

 

Когда выполняется отрицание по первому аргументу, получаем

 

                           

 

В соответствии с общим положением, у матрицы истинности происходит перестановка строк:

                           

      Y        

X

   0

  1

 0

   0     

  1

 1

    1

  1

 

 

                  

 

 

 

Значит, формула для рабочих блоков имеет вид

 

                                                           (7.19)

 

Аналогично, если выполняется отрицание по второму аргументу

 

                             

получаем перестановку столбцов исходной матрицы, что приводит к получению следующих результатов.

 

 

Матрица истинности этой операции

                                     

      Y        

X

   0

  1

 0

   1    

  1

 1

    1

  0

 

 

                  

 

 

 

а формула для рабочих блоков

 

                                                          (7.20)

Из этой таблицы получаем, что данная композиция совпадает по строению с операцией штокъюнкции (штрих Шеффера):

 

                                                                               ( 7.21)

 

Теперь можно рассмотреть композицию двух внутренних отрицаний для импликации

                                     

Для её матрицы истинности путём перестановки строк в предыдущей таблице, получим

                  

      Y        

X

   0

  1

 0

   1    

  0

 1

    1

  1

 

 

                  

 

 

 

что приводит к формуле для рабочих блоков:

 

                                                           (7.22)

Сравнивая эту формулу с (6.12), приходим к выводу:

 

                                                                            (7.23 )

Эта формула носит название закона контрапозиции импликации.

 

 

         Рассмотрим теперь внешнее отрицание импликации

 

                                     

Для неё получаем матрицу истинности

                                     

      Y        

X

   0

  1

 0

   0    

  0

 1

    1

  0

 

 

                  

 

 

 

Из этой таблицы следует связь этой операции с конъюнкцией

 

                                                                              (7.24)

 

Эта операция имеет также своё название «поляризация» и часто применяется в логике (особенно в теории множеств –  как вычитание).

Для поляризации принято обозначение:

 

                                                                                (7.25)

Эта формула читается: «Х» без «У», она указывает на исключение некоторых объектов из рассмотрения. По логическому смыслу поляризация является взаимной операцией для импликации.

 

г) Композиция эквиваленции с отрицанием.

Формула рабочих блоков эквиваленции

 

                           

 

Эквиваленция сама может быть рассмотрена как композиция двух взаимных импликаций:

 

                                                        (7.26)

 

Это легко проверить с помощью функции истинности.

Действительно:

 

            

 

Поэтому произведение этих функций, которое определяет конъюнкцию,

приводит к результату

 

                           (7.27)

 

Этот результат совпадает с формулой эквиваленции (9.3).

При отрицании эквиваленции по первому аргументу, получаем:

 

                  

Поэтому матрица истинности принимает вид           

                                     

      Y        

X

   0

  1

 0

   0    

  1

 1

    1

  0

 

                  

 

 

 

 

Это означает, что формула для рабочих блоков

        

                  

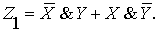
Полученная операция имеет самостоятельное значение и называется строгая дизъюнкция( или хартъюнкция). Она обозначается

 

                                                                                (7.28)

 

Легко проверить, что и отрицание эквиваленции по второму аргументу приводит к этой же операции, внутренне отрицание обоих аргументов снова даёт саму эквиваленцию, а её внешнее отрицание снова приводит к хартъюнкции (строгой дизъюнкции).

         Таким образом, мы рассмотрели все возможные композиции бинарных операций с отрицанием.

 

                   ЛИТЕРАТУРА:

 

1.     Ю.Л.Ершов, Е.А.Палютин. Математическая логика. СПб. «Лань»2005.

2.     И.А.Лавров, Л.Л.Максимова. Задачи по теории множеств, математической логике и теории алгоритмов. М. 1986 г.

 

3.     Евсеев В.И. О методике моделирования логических систем //Информационные технологии в образовании и науке, Казань, 2012. (225 – 231).