Математика/5. Математическое моделирование

                            к.ф.-м.н. доц.  В.И. Евсеев  

Казанский  (Приволжский) федеральный университет, Казань, Россия,

                          кафедра прикладной информатики

   УДК 681.32                        1 - vladislaw.evseev@yandex.ru, т.89047610772

 

О МОДЕЛИРОВАНИИ ЛОГИЧЕСКИХ ДОКАЗАТЕЛЬСТВ

 

 § 1. ОСНОВНЫЕ ВИДЫ  АКТОВ ДОКАЗАТЕЛЬСТВА

 

         Доказательность – одно из наиболее важных свойств правильного логического мышления. Структура доказательства включает в себя тезис, аргументы, демонстрацию или алгоритм доказательства, само доказательство и выводы или следствия из полученного результата.

         Обоснованием доказательства являются те положения, которые уже доказаны, или те, которые принимаются истинными без доказательства (например, аксиомы). В частности, мы будем использовать приведённые выше законы логики или некоторые следствия из них. Аксиоматический метод будет изложен в дальнейшем.

         Тезис – это предложение, истинность (или ложность) которого нужно доказать. В общем случае тезис может быть составленным из нескольких логически связанных предложений. По строению тезис может быть позитивным, утвердительным или негативным, отрицательным. Все составляющие тезиса должны быть однозначно понимаемы и отражать некоторую часть новых, ещё не полностью решённых задач.

         Аргументы – это факты или высказывания, истинность которых не вызывает сомнений, доказана или проверена опытом, что позволяет их использовать в процессе доказательства. В принципе, аргументы составляют совокупность логических формул, истинность которых известна.

         Формой доказательства (демонстрацией) называется способ логической связи между тезисом и аргументами. Эта связь должна быть обоснована на высказываниях, то есть, категорических суждениях и на правильной последовательности самих рассуждений (актов доказательства). Доказательство может быть прямым или косвенным. Существуют основные правила доказательства, которые представляют собой схемы или алгоритмы логически обоснованных рассуждений, а нарушение этих правил приводит к ошибкам в самих доказательствах и неправильным выводам, которые могут относиться к тезисам, аргументам или доказательствам Для обоснования тезиса обычно применяют две основные схемы, которые можно формализовать следующим образом:

а)  позитивное обоснование. Пусть даны А,В,С – известные истинные суждения (первичные аргументы), а Т – подлежащий доказательству тезис. Тогда схема прямого обоснования имеет вид:

 

                                                     (1.1).

 

б) негативное обоснование, содержащее исходно отрицание первоначального тезиса:

 

                                                                (1.2).

         Если все исходные аргументы объединить в виде первичной формулы (F), а тезис обозначить через Т, то можно получить схемы элементарных актов доказывания, для которых мы  рассмотрим только их  схематический вид.

         1)  эквивалентный позитивный однозначный акт

                   ,                                                           (1.3)

этот метод применяется в прямом доказательстве.  

         2) эквивалентный негативный однозначный акт

                   ,                                                           (1.4)

этот акт применяется в доказательстве от противного.                                  3) сопутственные позитивные многозначные акты:

         а) по прямой импликации

                   ,                                                           (1.5)

         б) по обратной импликации

                   .                                                            (1.6)

         4) сопутственные негативные многозначные акты:

         а) по прямой импликации

                   ,                                                           (1.7)

         б) по обратной импликации

                   .                                                           (1.8)

          5) альтернативные разделительные акты (в них используется операция нильюнкции):

         а) однозначный позитивный акт

                   ,                                                              (1.9)

         б) однозначный негативный акт

 

                   .                                                            (1.10)

 

         Иногда применяются условные линейные акты доказывания, которые являются по сути частными случаями рассмотренных, и мы не будем на них останавливаться.

 

 

         § 2. ОСНОВНЫЕ ВИДЫ   ТЕОРЕМ

        

         Теорема рассматривается как предложение, истинность которого должна быть обоснована строгим логическим доказательством. Доказательство – это демонстрация истинности утверждения путём применения аксиом, доказанных уже ранее теорем и следствий из них, вспомогательных предложений (лемм), а также логических законов. Такой подход позволяет строить обоснованную последовательность рассуждений (с возможным использованием формул, таблиц, графиков и т.п.), приводящих от условий теоремы к выводу о справедливости её утверждения. Сами условия теоремы – это совокупность исходных тезисов или посылок, которые характеризуют содержание теоремы, возможности её выполнения и предполагаемые действия при доказательстве. Формулировка теоремы – это утверждаемый тезис, требующий доказательства, а вывод рассматривается как последовательность формул и рассуждений, приводящих к самому доказательству.

         Исходные тезисы или посылки сами являются высказываниями из данного универсума   W. Обозначим эти посылки  Формула посылки имеет вид  Эта формула имеет область истинности и область ложности, которые мы обозначим соответственно() и  Очевидно, что

                            () +  = W.                                                  (2.1)

Формулировка теоремы является данной логической функцией T от нескольких утверждений  (высказываний)  , которые сами  связаны известными логическими функциями с исходными тезисами:

 

               

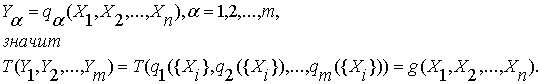
Следовательно, утверждение теоремы также содержит указанные высказывания, но под знаком  сложной логической формулы .  Для неё области истинности и ложности обозначим аналогично предыдущему: () и  

         Теперь перейдём к видам теорем, которые обычно применяются в математической логике. Первый вид – это прямая теорема: «Из посылки следует утверждение ». При этом требование доказательности имеет простой вид:

 

                                      ()  () .                                                (2.2)

Это условие проще всего проверять табличным методом: с помощью матриц Карно соответствующего вида. Прямая теорема может быть записана в форме правила вывода:                  

        

  

       условие

     доказательности:

  ()  ()

  

 

Вторым видом является обратная к исходной теорема, в которой исходные посылка и утверждение меняются местами: «Из посылки  следует утверждение  ». Требование доказательности в этом случае имеет вид:

                                      ()   () .                                     (2.3)

        

Мы не будем записывать её в форме правила вывода. Если выполняется равенство для областей истинности:

 

                            () = (),                                                   (2.4)

то мы приходим к понятию необходимых и достаточных условий, то есть, эквивалентности данных формул:

 

                    .                           (2.5)

 Третьим видом рассматривается теорема, противоположная данной: «Из отрицания  посылки  следует отрицание утверждения ».

         Для этого вида теоремы условия доказательности записываются с применением областей ложности данных формул:

        

                                                                              (2.6)

 

Соответственно этому можно записать форму правила вывода:

 

 

  

       условие

     доказательности:

      

  

        

Четвёртым видом является теорема, противоположная обратной, которая имеет вид: «Из отрицания  посылки  следует отрицание утверждения  ». В условии доказательности по сравнению с предыдущим меняются местами левая и правая части:

 

                              .                                                (2.7)

 

В этом случае мы также не будем записывать соответствующее правило вывода ввиду его очевидности.

 

§ 3. О ДОКАЗАТЕЛЬСТВАХ ЗАКОНОВ ЛОГИКИ.

 

         Мы будем условно подразделять все законы логики по уровням, соответствующим вхождению первичных высказываний. Таким образом, мы рассмотрим унарные, бинарные и тернарные законы, а также переходные формы законов, отражающие расширение или сжатие исходной формулы.     Существуют и законы более высоких уровней, но в данном пособии мы   не будем их рассматривать. Если закон состоит из равенства (тождества) двух частей, то удобно рассматривать каждую часть отдельно и затем сравнивать формулы рабочих блоков или матрицы Карно этих частей. Их совпадение приводит к доказательству закона. Если закон представляет собой тавтологию, то есть всюду верное высказывание, то достаточно показать, что функция истинности этого высказывания равна единице. Если же закон имеет вид последовательности импликаций, то для его доказательства нужно построить соответствующие части: посылку (причину) и результат (следствие). Затем проводится сравнение матриц Карно этих высказываний для выявления правильности следования или же определения дефектных блоков. Перейдём к рассмотрению основных логических законов.

 

1. Унарные (однослойные) законы.

 

1.1. Закон непротиворечивости:

 

                  

1.2. Закон тождества:

 

                  

1.3.Закон исключенного третьего:

 

                  

1.4.Закон введения отрицания:

 

                  

1.5. Закон снятия двойного отрицания:

 

                  

1.6. Законы идемпотентности:

                  

                               

 

 

         Не останавливаясь на доказательствах простейших законов, приведём пример доказательства для закона 1.4.

         Обозначим левую часть     

Для неё получаем:

 

                  

 

Этот результат утверждает справедливость данного закона.

 

2. Бинарные (двухслойные) законы. Они содержат два исходных высказывания и устанавливают основные соотношения этого уровня.

 

2.1. Законы коммутативности конъюнкции и дизъюнкции.

 

                           

 

2.2. Закон контрапозиции:

 

                           

 

2.3.Закон обратной контрапозиции:

 

                           

 

2.4. Закон отрицания импликации:

 

                  

 

2.5. Законы де Моргана:

 

                  

 

 

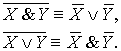
2.6. Законы взаимосвязи бинарных операций:                                                         

                                  

 

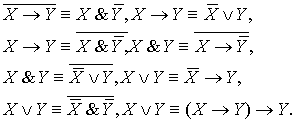
Доказательство этих формул предоставляем читателям.

 

         3. Тернарные (трехслойные) законы.

Они содержат три исходных высказывания и устанавливают основные закономерности этого уровня. В реальности таких законов очень большое количество, поэтому мы рассмотрим только основные из них.

 

         3.1. Законы ассоциативности конъюнкции и дизъюнкции:

 

        

 

         3.2. Законы дистрибутивности конъюнкции и дизъюнкции:

 

        

 

         3.3.Законы импликации:

        

        

 

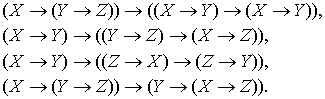
         3.4. Законы переноса:

        

         а) закон импортации

 

        

 

         б) закон экспортации

 

        

 

         3.5. Законы монотонности:

 

        

 

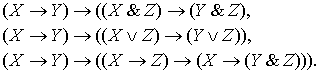
         3.6. Законы сложной контрапозиции:

        

        

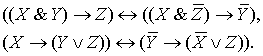
         3.7. Законы силлогизма:

 

        

 

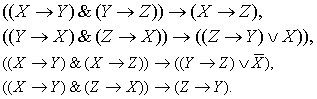
 Выражения для второй,  третьей и четвёртой  фигур силлогизма указываются в исправленной форме.

 

3.8. Законы выявления:

 

 

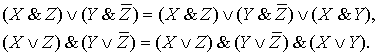
         4. Рассмотрим примеры доказательства некоторых из  приведённых законов, предоставляя возможность читателю по предлагаемым схемам провести исследование других законов.

         Докажем справедливость второго из законов сложной контрапозиции:

                  

 

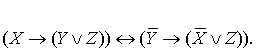
         Для доказательства найдем функции истинности левой и правой частей и покажем их совпадение.

         Введем обозначения:

 

        

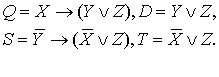
Теперь последовательно получаем для левой части:

 

        

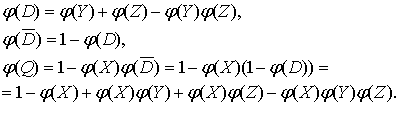
Аналогично для формулы в правой части получаем последовательно,

учитывая введенные обозначения:

 

                  

                  

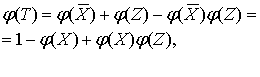
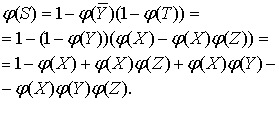
         Таким образом, значения функций истинности в левой и правой частях совпадают, что означает справедливость рассматриваемой формулы.

 

 

 

 ЛИТЕРАТУРА:

 

 

1.     Ю.Л.Ершов, Е.А. Палютин. Математическая логика. СПб. 2005.

2.     Дж.Шенфилд. Математическая логика. М.«Наука». 1975

3.     Евсеев В.И. Логика. Монография. «ТАРИ». Казань. 2001.