Математика/5. Математическое моделирование

к.ф.-м.н. доц. В.И. Евсеев

Казанский (Приволжский) федеральный университет, Казань, Россия,

кафедра прикладной информатики

УДК 681.32 1 - vladislaw.evseev@yandex.ru, т.89047610772

О МАТРИЧНЫХ ПРЕДСТАВЛЕНИЯХ НОРМАЛЬНЫХ ФОРМ

§ 1. Уровни нормальных квадратичных форм

В общем случае нормальная квадратичная форма может быть представлена как композиция четырех исходных суждений, построенная по определенной схеме, каждая схема характеризуется своим уровнем формы:

(1.1)

Для таких форм естественно определяются все ранее рассмотренные логические операции: если дан набор высказываний то их элементарным конъюнктом (или конъюнктивным одночленом) называется высказывание

. (1.2)

Аналогично, их элементарным дизъюнктом (или дизъюнктивным одночленом) называется высказывание вида

(1.3)

Дизъюнкция конъюнктивных одночленов называется дизъюнктивной нормальной формой (д.н.ф.), её можно записать в виде формулы

(1.4)

Аналогично, конъюнкция дизъюнктивных одночленов называется конъюнктивной нормальной формой (к.н.ф.), и её формула:

(1.5)

Заметим, что дизъюнктивная нормальная форма для трёх и четырёх переменных нами фактически использовалась при записи рабочих блоков в матрицах Карно.

Конъюнктивная нормальная форма является её двойственным представлением и выглядит несколько искусственно. Эти нормальные формы применяются для синтеза микросхем.

Нормальная форма называется совершенной, если в каждый её элементарный конструкт входят все исходные высказывания (возможно – с внутренними отрицаниями).

2. Остановимся теперь на случае квадратичных нормальных форм. В этом параграфе мы рассмотрим строение дизъюнктивных нормальных форм от четырех переменных. Для них мы получаем следующие слои элементарных конъюнктов:

а) первый уровень – одноместные конъюнкты

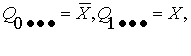
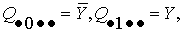(1.6)

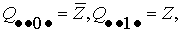
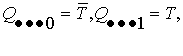
б) второй уровень – двуместные конъюнкты

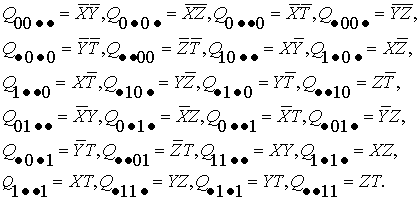(1.7)

в) третий уровень – трёхместные конъюнкты

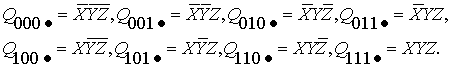(1.8)

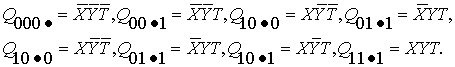
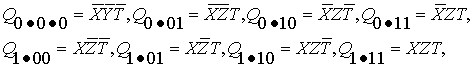
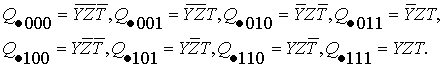
Таким образом, любой квадратичный конъюнкт можно представить в виде индексной записи , где индексы принимают значения из множества элементов .

Поэтому квадратичная дизъюнктивная нормальная форма имеет вид последовательности дизъюнкций:

(1.9)

Частным случаем дизъюнктивной нормальной формы является совершенная нормальная форма, в которой каждая переменная (высказывание) встречается в каждом элементарном конъюнкте только один раз.

г) четвертый уровень: для полных квадратичных конъюнктов вводится также сокращённая запись, соответствующая десятичной индексации (вместо двоичной). Применяя её, получим:

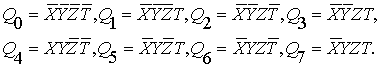(1.10)

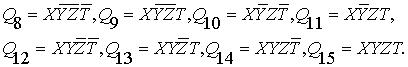
Именно такие выражения мы применяем при построении матриц Карно для квадратичных операций.

§ 2. Матричные представления нормальных квадра-форм.

Для структурирования матриц Карно квадра-форм необходимо применять тождества Канта, соответствующие уровням рассматриваемых универсумов. Универсум четвертого уровня представляет собой прямую сумму шестнадцати блоков, входящий в нормальные формы этого уровня:

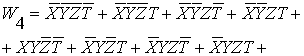
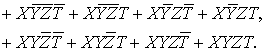(2.1)

Четыре универсума третьего уровня строятся для всех случаев нормальных форм этого уровня, поэтому мы приведем лишь первый из них.

(2.2)

Существует шесть типовых универсумов второго уровня, из которых также укажем только один:

(2.3)

Также из четырех типовых универсумов первого уровня приведем лишь один:

. (2.4)

Матричное представление нормальных форм находятся как конъюнкции нормальной квадратичной формы соответствующего уровня и универсума этого же уровня. Так, для нормальной формы первого уровня

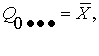
строим взаимный универсум третьего уровня:

При этом получаем вид матричной записи:

(2.5)

Матрица Карно в этом случае имеет вид:

T		0	0	1	1
Z	Y X	0	1	0	1
0	0	1	1	1	1
0	1	0	0	0	0
1	0	1	1	1	1
1	1	0	0	0	0

Аналогично можно получить матричное представление для нормальной формы первого уровня. Если, например, взять нормальную форму первого уровня

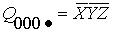(2.6)

И составить для нее конъюнкцию

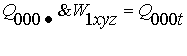
то получим результат:

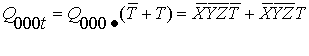(2.7)

Эта операция имеет матрицу Карно:

T		0	0	1	1
Z	Y X	0	1	0	1
0	0	1	0	0	0
0	1	0	0	0	0
1	0	0	0	1	0
1	1	0	0	0	0

Наибольший интерес здесь представляют нормальные формы второго уровня, так как с их помощью можно получить квадратичные представления бинарных операций, что в дальнейшем позволяет выделить те квадра-операции, которые можно представить в виде композиций бинарных операций.

Позволим себе привести один предварительный пример.

Пусть выбрана нормальная квадра-форма второго порядка:

. (2.8)

Соответствующий дополняющий универсум второго порядка имеет вид

.

В этом случае находим квадратичное представление:

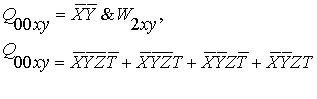(2.9)

Эта квадра-форма представляется матрицей Карно:

T		0	0	1	1
Z	Y X	0	1	0	1
0	0	1	0	1	0
0	1	0	0	0	0
1	0	1	0	1	0
1	1	0	0	0	0

Заметим, что рассматриваемая бинарная операция является нильюнкцией

, (2.10)

а соответствующее квадратичное представление обозначим

(2.11)

§ 3. Квадратичные представления бинарных операций

1.Как показано в последнем примере, для выбранной бинарной операции строится ее конъюнкция с дополняющим универсумом второго порядка, что приводит к искомому квадратичному представлению.

Рассмотрим эти представления для основных бинарных операций: конъюнкции, дизъюнкции, импликации (правой) и экваваленции. Остальные бинарные операции являются внешними отрицаниями указанных, значит, в их матрицах автоматически происходит замена нулей на единицы.

Перейдём к построению матриц Карно основных бинарных операций.

Для конъюнкции получаем исходный вид формулы:

(3.1)

Соответствующая квадра-форма является композицией:

(3.2)

Таким образом, получаем:

(3.3)

Теперь строим матрицу Карно для этой операции:

T		0	0	1	1
Z	Y X	0	1	0	1
0	0	0	0	0	0
0	1	0	1	0	1
1	0	0	0	0	0
1	1	0	1	0	1

На основе полученного результата можно сразу построить матрицу Карно для взаимной с конъюнкцией бинарной операции – штокъюнкции, но мы не будем на этом останавливаться.

2. Найдем квадратичное представление для дизъюнкции:

(3.4)

Формула Канта для этой операции имеет вид:

(3.5)

Поэтому получается квадратичное представление дизъюнкции:

. (3.6)

Подставляя в эту формулу выражение дополняющего универсума, находим выражение искомого представления:

(3.7)

Осталось только раскрыть скобки и записать явный вид этой квадра-формы.

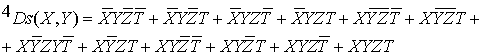(3.8)

Матрица Карно для дизъюнктивной квадра-формы принимает вид

T		0	0	1	1
Z	Y X	0	1	0	1
0	0	0	1	0	1
0	1	1	1	1	1
1	0	0	1	0	1
1	1	0	1	0	1

Отметим, что уже рассмотренная нильюнкция является взаимной операцией для дизъюнкции, и её матрица Карно в сумме с матрицей дизъюнкции составляет полное правильное покрытие всего универсума четвертого уровня. 3. Рассмотрим типичную правую импликацию, заданную своей формулой Карно:

(3.9)

Для нее квадратичное представление имеет вид:

(3.10)

Вычисления представляются формулой Канта.

(3.11)

После раскрытия скобок приходим к результату:

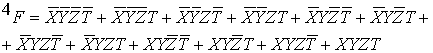(3.12)

Теперь можно построить матрицу Карно для этой операции:

T		0	0	1	1
Z	Y X	0	1	0	1
0	0	1	1	1	1
0	1	0	1	0	1
1	0	1	1	1	1
1	1	0	1	0	1

Заметим, что матрица взаимной (левой) импликации является относительно построенной, а в матрице соответствующего (левого) поляроида происходит «ротация» нулей и единиц.

4. Эквиваленция рассматривается как конъюнкция двух взаимных импликаций

(3.13)

Мы считаем известной формулу Канта для этой операции:

. (3.14)

Таким образом, квадратичное представление эквиваленции характеризуется следующей формулой:

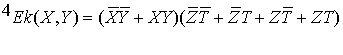(3.15)

После раскрытия скобок получаем матрицу Канта для этого квадратичного представления.

T		0	0	1	1
Z	Y X	0	1	0	1
0	0	1	0	1	0
0	1	0	1	0	1
1	0	1	0	1	0
1	1	0	1	0	1

Взаимная к эквиваленции бинарная операция называется хартъюнкцией (или строгой дизъюнкцией) и определяется формулой Канта:

. (3.16)

Матрица Карно для ее квадратичного представления отличается от матрицы эквиваленции «ротацией» нулей и единиц, поэтому мы не будем ее здесь приводить.

ЛИТЕРАТУРА

1. Ю.Л.Ершов, Е.А. Палютин. Математическая логика. СПб. 2005.

2. Дж.Шенфилд. Математическая логика. М.«Наука». 1975

3. Евсеев В.И. Логика. Монография. «ТАРИ». Казань. 2001.