Математика/5. Математическое моделирование

к.ф.-м.н. доц. В.И. Евсеев

Казанский (Приволжский) федеральный университет, Казань, Россия,

кафедра прикладной информатики

УДК 681.32 1 - vladislaw.evseev@yandex.ru, т.89047610772

ОБ АЛГОРИТМЕ ПОСТРОЕНИЯ ДОКАЗАТЕЛЬСТВА

§ 1. Построение алгоритма доказательства.

Для поверки правильности формулировки доказываемого предложения и самой содержательной стороны доказательства, как следует из приведенного ранее анализа, необходимо выполнить следующие логически взаимосвязанные шаги.

1) Нормализация формул посылки и следствия из нее. Это значит, что формулу посылки нужно привести к виду формулы Канта или нормальной дизъюнктивной формы, что позволяет точно определить количество реально входящих переменных, то есть, порядок операции.

Точно также нужно поступить и с формулой, требующей доказательства. Если их порядки совпадают, то можно по принципу импликативной формы доказательства приступить к сравнению значений у этих формул.

2) Если порядки формул посылки и следствия не совпадают, то к меньшей по своему порядку формуле применяют метод расширения до установления равенства порядков в обеих формулах.

3) Само расширений состоит в применении нейтральных унарных сомножителей при построении конъюнктов в нормальной дизъюнктивной форме. Каждый нейтральный сомножитель состоит из прямой суммы взаимных классов (например (). Таким способом строятся расширенные формулы необходимого порядка.

4) Для формул одного прядка имеющих вид нормальных дизъюнктивных форм, проводится сравнение значений элементов их матриц по критерию импликации. Так, условие правильности импликации

(1.1)

имеет матричный вид:

. (1.2)

5) Затем проводится сравнение значений всех блоков построенных матриц с целью фиксации «дефектных» блоков, в которых условия правильной импликации не выполняются.

6) Если импликация не содержит «дефектных» блоков, то доказательство завершается выводом и правильности формулировки исходного положения, если же имеются такие блоки, в которых условия (1.2) не выполняются, то необходимо исправить или переформулировать исходную теорему, что иногда бывает непросто сделать. Если же найдена исправленная формулировка предложения, то новую формулировку нужно снова проверить по тем же критериям.

7) Окончательная формулировка теоремы как закона логики.

§ 2. Применение алгоритма доказательства

В качестве примеров исследуем фигуры силлогизма в имликативной форме.

Первая фигура силлогизма может быть представлена в следующей импликативной форме:

(2.1)

Для левой стороны этой фигуры получаем структурные формулы

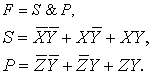(2.2)

Таким образом, получаем

(2.3)

что приводит к матрице Карно:

Z	Y X	0	1
0	0	1	1
0	1	1	0
1	0	0	0
1	1	0	1

Вторая сторона импликации

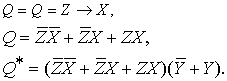(2.4)

Значит, для расширенной матрицы получаем формулу Канта:

(2.5)

откуда следует матрица Карно:

Z	Y X	0	1
0	0	1	1
0	1	1	1
1	0	0	0
1	1	1	1

Выполнение условий правильности вывода этой импликации очевидна:

. (2.6)

Теперь изучим вторую фигуру силлогизма в импликативной форме:

(2.7)

В данном случае получаем последовательность бинарных операций: (2.8)

Для внутренних бинарных операций и их отрицаний получаем:

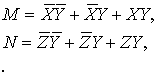(2.9)

Поэтому для их конъюнкции

(2.10)

Для правой стороны этой импликации находим:

(2.11)

Так как это лишь бинарная формула, то ее следует расширить до тернарной путем нейтральной конъюнкции с унарной формой

(2.12)

В результате получаем расширенную (псевдо тернарную) операцию:

(2.13)

. (2.14)

Теперь укажем явный вид матриц этих операций

Z	Y X	0	1
0	0	1	1
0	1	1	1
1	0	0	0
1	1	1	1

Z	Y X	0	1
0	0	1	1
0	1		1
1	0	0	0
1	1	0	1

Следовательно, вторая фигура силлогизма является законом логики, так как всюду выполняется условие правильности импликации:

(2.15)

Здесь мы продемонстрировали работу предложенного алгоритма для случаев, когда исходные формулы оказываются законами логики и не требуют изменений.

§ 3. Проверка наличия дефектных блоков с помощью алгоритма.

Так как правая сторона импликативной формулы для всех исходных видов фигур силлогизма одинакова, то для случаев третьей и четвертой фигур силлогизма распишем только левую сторону, а потом будем сравнивать ее уже с известной формулой.

Исходную формулу для третьей фигуры рассмотрим в виде

(3.1)

Для ее левой части получаем структуру:

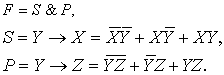(3.2)

Поэтому формула Канта принимает вид:

(3.3)

это приводит к матрице Карно:

Z	Y X	0	1
0	0	1	1
0	1		1
1	0	0	0
1	1	0	1

Сравнение с матрицей приводит к выводу о наличии «дефектного» блока

. (3.4)

В.И.Лобанов в предложил следующее исправление импликативной формы третьей фигуры:

(3.5)

Для исправленной формулы распишем вид правой части, так как левая часть совпадает с данной в исходной фигуре.

Правая часть здесь структурируется следующим образом:

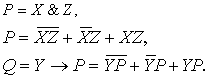(3.6)

Поэтому формула Канта здесь следующая:

(3.7)

То есть, совпадает со значением левой части в исходном виде:

. (3.8)

Четвертая фигура силлогизма исходно такова:

(3.9)

Известным уже способом получаем здесь формулу Канта:

(3.10)

что позволяет записать матрицу Карно:

Z	Y X	0	1
0	0	1	0
0	1	0	0
1	0	1	1
1	1	0	1

Следовательно, эта фигура имеет два «дефектных» блока:

, (3.11)

Слегка изменив вариант В.И.Лобанова для третьей фигуры, найдем подобное исправление и для четвертой фигуры:

(3.12)

Проведя расчет для данного вида правой части фигуры, получим:

. (3.13)

Матрица Карно здесь принимает вид:

Z	Y X	0	1
0	0	1	1
0	1	1	1
1	0	1	1
1	1	0	1

Отсюда сразу следует выполнение условий правильности построенной импликативной последовательности.

ЛИТЕРАТУРА:

1. Ю.Л.Ершов, Е.А. Палютин. Математическая логика. СПб. 2005.

2. Дж.Шенфилд. Математическая логика. М.«Наука». 1975

3. Евсеев В.И. Логика. Монография. «ТАРИ». Казань. 2001.