Математика/5. Математическое моделирование
Канд. техн.
наук Пономарев Д.Ю.
Сибирский
государственный аэрокосмический университет им. акад. М.Ф. Решетнева, Россия
Контурный метод тензорного анализа инфокоммуникационных сетей
Исследование вероятностно-временных
характеристик (ВВХ) инфокоммуникационных сетей и систем, к которым относится и
сеть Интернет, является одной из актуальных задач развития современных
инфокоммуникаций, т.к. именно данные характеристики позволяют оценить качество
обслуживания (QoS – Quality of Service)
информационных потоков в данных сетях. Оцениваемыми параметрами при этом
являются: вероятность потери пакета, среднее время задержки пакета в системе,
вариация времени задержки пакета. С момента построения сети ARPANET задача исследования ВВХ является одной из основных и
с развитием технологий сетей передачи данных остается актуальной. Однако проектирование рассматриваемых сетей может
быть затруднено трудоемкостью расчетов параметров оборудования, при которых
необходимый уровень QoS будет поддерживаться на
заданном уровне, что усложняется как сложной топологией таких сетей, так и
использованием дополнительных протоколов обработки на различных уровнях модели
взаимодействия открытых систем (ВОС).
Для оценки ВВХ сетей связи в данной работе
применяется математический аппарат преобразования координат (т.е. тензорный
анализ сетей [1]), рассматривая сети, как геометрические объекты, проекции
которых в различных системах координат различны, но физические свойства самих
объектов при этом не меняются. Основоположником тензорного анализа сетей
является Г. Крон [1], который впервые использовал тензорный анализ и топологию
в приложении к теории электрических сетей. Дальнейшее развитие идеи тензорного
анализа, в т.ч. и для информационных систем, получили в работах Петрова А.Е
[1], Петрова М.Н. [2], Лемешко А.В. [3] и др. Основополагающими в теории
Г.Крона являются два постулата, смысл которых заключается в том, что,
во-первых, объединение элементов не вводит никаких новых физических явлений,
ненаблюдаемых в примитивном элементе, а уравнение, описывающее поведение
сложной системы записывается аналогично уравнению состояния примитивного
элемента только в матричном виде; и, во-вторых, при изменении структуры сложной
системы изменяются только элементы матричного уравнения, а переход к описанию
новой структуры осуществляется с помощью матрицы перехода.
Для исследования инфокоммуникационных
сетей аксиомы тензорного анализа сетей сформулируем следующим образом.
Процессы обслуживания информационных
потоков в системах распределения информации, описываемые моделями теории
массового обслуживания, в основном определяются дисциплиной обслуживания
частной системы и, поэтому, анализ распределения трафика в сети может быть
проведен с использованием известных выражений для простейшего элемента и
дальнейшим их использованием в уравнении для сети путем замены величин входящих
в данные выражения на матричные переменные соответствующей размерности. Смысл
этой аксиомы заключается в том, что уравнения, описывающие процессы,
протекающие в сложной системе (сети), могут быть получены из уравнений
простейших элементов системы, так как при объединении элементов в систему не
возникают новые физические явления, в системе происходят те же процессы что и в
простых элементах. Таким образом, тензорная методология позволяет находить
параметры сложных систем (т.е. сетей) путем анализа их частей или проектировать
новые сети за счет объединения ранее исследованных. При анализе
инфокоммуникационных сетей в данной работе используется выражение для
определения загрузки системы.
Следующая аксиома тензорного анализа
формулируется так: описание инфокоммуникационных сетей, содержащих n систем
распределения информации, в разных системах координат содержит одинаковое число
матричных переменных и имеет одинаковый вид. Отличия заключаются лишь в
численных значениях элементов матричных переменных, таких как: загрузка,
длительность обслуживания, среднее число требований и т.д. При этом переход от
одной системы координат к другой производится использованием матриц перехода,
получение которых является простой и легко формализуемой процедурой. Таким
образом, для любой инфокоммуникационной сети существует возможность провести
простую процедуру преобразования для рассмотрения задачи оценки ВВХ в такой
системе координат, которая является более удобной для наблюдения и
исследования, при этом численные значения матричных переменных изменяются по
известному алгоритму. Причем новая система координат позволяет легко составлять
уравнения состояния элементов. Для применения полученных в результате анализа
уравнений к исходной системе следует вернуться к первоначальной системе
координат.
В качестве уравнения состояния в данной
работе выбрано выражение, определяющее загрузку инфокоммуникационных систем: 
В таком случае,
возбуждение сети производится контурными интенсивностями 
,
вызывающими в сети отклик в виде загрузок сети. Примитивная контурная сеть
состоит из контуров не связанных непосредственно между собой [4]. Количество
систем в примитивной сети равно количеству систем в исходной сети.
Геометрическими объектами, необходимыми
для описания такой примитивной сети, являются: вектор интенсивности потоков
вызовов в системах 
,
вектор загрузки систем распределения информации 
,
тензор средней длительности обслуживания 
.
Вектор интенсивности потоков вызовов
записывается, как: 
(
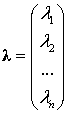- интенсивности информационных потоков)ю В общем виде, вектор загрузки систем
распределения информации, определяется, как: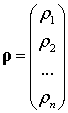 
(
- загрузки систем распределения информации). Тензор средней длительности
обслуживания записывается, как квадратная матрица размерностью n-столбцов на n-строк,
элементы по главной диагонали которой равны средней длительности обслуживания в
системах распределения информации, другие элементы характеризуют взаимное
влияние систем друг на друга, а при отсутствии влияния они равны нулю: 
Тогда, уравнение состояния для примитивной
сети, в общем случае, имеет вид: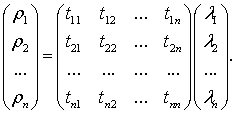 
Во вспомогательной системе координат
исходная сеть заменяется контурной сетью, которая получается при объединении
систем, составляющих примитивную сеть.
Далее, необходимо определить тензор и
формулы преобразования. Тензор преобразования это геометрический объект,
связывающий переменные исходной и вспомогательной сети [1]. Уравнение
преобразования тогда записывается, как [4]: 
где 
– вектор интенсивности поступления вызовов
для примитивной сети; 
– вектор контурных интенсивностей поступления
вызовов; 
– тензор преобразования интенсивностей
потоков.
Тензор преобразования определяет
преобразование координат при переходе от примитивной к вспомогательной системе.
В матричной форме тензор преобразования можно записать, как (k - число контуров):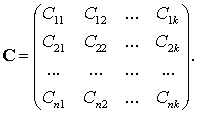 
Элементы i-ой строки матрицы показывают контурные потоки,
проходящие через i-ую систему распределения
информации, элементы j-го столбца
содержат информацию о системах входящих в j-ый контур.
Для нахождения элементов матрицы
преобразования в вспомогательной сети рассматриваются контурные интенсивности
потоков контуров и для каждой системы они выражаются через интенсивности
примитивной сети в соответствии с их местом в исходной.
При этом, для вспомогательной сети
уравнение состояния приобретает вид: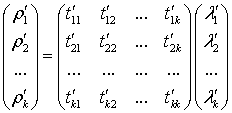 
или 
Для установления формул преобразования
геометрических объектов используются следующие предположения. Во-первых, что
поток вызовов с одной и той же интенсивностью (λ) поступления вызовет при
неизменной интенсивности обслуживания одну и ту же загрузку (ρ) устройств при
изменении структуры и можно считать, что будет выполняться соотношение
(инвариант): 
где переменные
со штрихом для вспомогательной структуры сети (содержащей информацию о
топологии исходной сети), без штриха для декомпозиционной структуры сети
(примитивной сети). Во-вторых, объединение систем в единую сеть не вызывает
никаких изменений процесса обслуживания информационного потока, т.е. тогда
анализ любой сложной системы (сети) будет связан с определением простейшего
элемента, его свойств и переносом алгоритма анализа на всю сложную систему
(сеть). В-третьих, изменение структуры сети не предполагает качественное
изменение основных соотношений между физическими величинами, описывающими
простейший элемент, а определяет только их численное изменение.
Тогда, с учетом топологии интенсивности
примитивной сети можно задать с помощью матрицы перехода, как: 
Следовательно, используя данное выражение, можно выразить загрузки
исходной сети через загрузки примитивной или декомпозиционной сети: 
Далее, 
Таким
образом, правило преобразования загрузок: 
Тогда, для нахождения правила
преобразования для матрицы средней длительностей обслуживания, используем
уравнение состояния для примитивной сети (
): 
Откуда,
выражая загрузку: 
Следовательно,
правило нахождения тензора средней длительности обслуживания записывается, как:
Таким образом, уравнение состояния вспомогательной
сети приобретает следующий вид:
. (1)
Используя данное матричное уравнение можно
оценить ВВХ инфокоммуникационной сети. Для этого необходимо решить уравнение
(1) относительно 
. Для нахождения распределения трафика по сети,
находим вектор интенсивностей потоков в сети, как: 
Откуда,
загрузка для каждой системы определяется, как: 
.
Для оценки ВВХ используем известные выражения для нахождения вероятности
состояний систем 
,
среднего числа требований в системе 
и среднее время задержки 
,
определяемые, как функциональные зависимости от загрузки 
в соответствии с выбранной дисциплиной
обслуживания системы распределения информации.
В заключение можно сделать следующие
выводы. Во-первых, уравнения, описывающие процессы, протекающие в
инфокоммуникационной сети могут быть получены из уравнений простейших элементов
системы, так как при объединении элементов в систему не возникают новые
физические явления, в сети происходят те же процессы что и в простых элементах.
Во-вторых, описания инфокоммуникационных сетей в разных системах координат
содержит равное число матричных переменных и имеет одинаковый вид. Таким
образом, для любой инфокоммуникационной сети существует возможность провести
простую процедуру преобразования для рассмотрения задачи оценки ВВХ в такой
системе координат, которая является более удобной для наблюдения и
исследования, при этом численные значения матричных переменных изменяются по
известному алгоритму. Представленные результаты демонстрируют широкие
возможности тензорного анализа по исследованию инфокоммуникационных сетей,
особенно при больших масштабах сетей. Также, следует отметить хорошую
формализуемость алгоритма контурного метода [4].
Литература:
1.
Петров А.Е. Тензорная
методология в теории систем. – М.: Радио и связь, 1985.
2.
Веревкина Е.В., Захарченко М.О., Петров М.Н. Тензорная методология в
информационных сетях. Красноярск: НИИ СУВПТ, 2001.
3.
Лемешко
А. В., Евсеева О. Ю. Тензорная геометризация структурно-функционального
представления телекоммуникационной системы в базисе межполюсных путей и
внутренних разрезов // Наукові записки УНДІЗ. - Вип. 1(13). - 2010. - С. 14-26.
4.
Пономарев Д.Ю. Тензорная методология в информационных
коммуникациях // Известия высших учебных заведений. Приборостроение. –
2012. – Т. 55. – № 5. – С. 18-23.