Работа на конкурс
научных работ
студентa 5 курса ФМФ
Лесосибирского
педагогического института – филиала
ФГАОУ ВПО
«Сибирский федеральный
университет»
Тарасюка Е.Н
Прогрессии в
геометрических задачах
Научный
руководитель –
ст.
преподаватель кафедры ВМиИ
Лесосибирского
педагогического института –
филиала ФГАОУ ВПО
«Сибирский
федеральный университет» Игнатьева
Н.К.
Прогрессии в геометрических
задачах
Тема
«Арифметическая и геометрическая прогрессии» изучается в разделе «Алгебра»,
поэтому геометрические задачи на прогрессии вызывают у учащихся с одной стороны
интерес, а с другой стороны - некоторые затруднения при поиске пути решения.
Среди задач указанного типа можно выделить два вида:
1. Задачи на нахождение
неизвестных элементов в треугольниках, стороны или углы которых образуют
прогрессии.
2. Задачи, в условии
которых ничего не говорится о прогрессиях,
то есть учащимся нужно самостоятельно догадаться о необходимости их
использования при решении задачи.
Приведем
несколько примеров задач первого и второго типа.
Задача 1 [1:56]. Стороны прямоугольного треугольника образуют
арифметическую прогрессию. Найти стороны треугольни
ка.
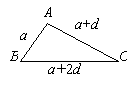Решение:
Пусть наименьший катет 
, тогда второй катет 
и гипотенуза 
где 
- разность прогрессии, 
.
По теореме Пифагора 
или 
. Решая это однородное уравнение, получим 
и 
(не удовлетворяют условию задачи). Имеем, 
, 
( где 
- любое число), то есть условию задачи удовлетворяют
прямоугольные треугольники, подобные египетскому.
Задача 2 [1:74]. Сторона квадрата
равна 
. Середины сторон этого квадрата соединили отрезками.
Получился новый квадрат. С новым квадратом поступили точно так же, как и с
предыдущим, и т.д. Найти предел суммы периметров и предел суммы площадей этих
квадратов
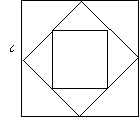Решение: Найдем длину стороны
нового квадрата, если сторона предыдущего квадрата равна/ 
. Так как сторона
нового квадрата – это гипотенуза равнобедренного прямоугольника с катетами 
, то она равна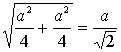 
. Следовательно, сумма периметров 
и сумма площадей 
всех образующих квадратов будут равны
и 
представляют собой суммы бесконечно убывающих прогрессий со
знаменателями
и 
соответственно.
Поэтому,
,
.
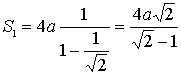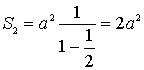Ответ: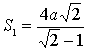 
, 
.
Задача 3 [3:56]. Длины сторон 
, 
и 
треугольника
образуют в указанном порядке арифметическую прогрессию. Найти во
сколько раз высота треугольника 
,
опущенная из вершины 
на
сторону 
,
больше радиуса вписанной в этот треугольник окружности.
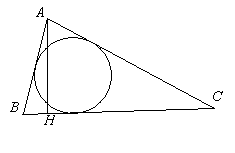
Решение: Рассмотрим треугольник 
и
проведем в нем высоту 
. Зная, что стороны AB, BC, AC треугольника ABC образуют в указанном
порядке арифметическую прогрессию, введем следующие обозначения. Пусть AB
,
тогда BC
, a AC
.
Здесь 
–
это разность арифметической прогрессии. Теперь запишем формулы для вычисления
площади треугольника. Площадь
треугольника АВС можно
вычислить с помощью высоты, проведенной из вершины A к стороне BC.
Имеем: 
С другой стороны, площадь треугольника АВС можно вычислить с помощью полупериметра и радиуса вписанной в
этот треугольник окружности:
Полученные
для площади треугольника 
выражения можно
приравнять. Будем иметь 
= 
Сократив
левую и правую часть полученного уравнения на 
,
получим 
= 
Откуда
Задача 4 [2:74] В окружность
радиусом 
вписан правильный треугольник, в треугольник вписана
окружность, в окружность снова вписан правильный треугольник, и т.д. Найти
сумму периметров всех правильных треугольников.
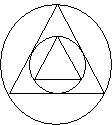Решение: Так как радиус вписанной в правильный
треугольник окружности в два раза меньше радиуса описанной около этого
треугольника окружности, то радиус окружности, описанной около треугольника 
(
)
в два раза больше радиуса окружности, описанной около треугольника 
(
)
. Он же в свою очередь в два раза больше радиуса окружности, описанной около
треугольника 
(
),
и т.д. (
).
Выразим
стороны правильных треугольников через радиусы описанных около них окружностей
по формуле 
. Тогда имеем:
,
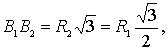
и т.д.
Периметры
соответствующих треугольников равны: 
и т.д.
Сумма периметров треугольников 
+… представляет собой сумму бесконечно убывающей
геометрической прогрессии со знаменателем 
и первым членом 
.
С помощью формулы суммы бесконечно убывающей
геометрической прогрессии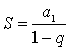 
находим, что 
=
.
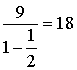Ответ: 18.
Таким
образом, мы получили, что высота треугольника в три раза больше радиуса
вписанной в этот треугольник окружности.
Анализируя решения задач, можно заметить, что
основная сложность содержится в задачах второго типа – трудно увидеть
прогрессию в задачах, в условии которых ничего о них не сказано. Целесообразность их изучения связана с тем, что обучение учащихся дополнительному материалу по
содержательно-методической линии
прогрессии в геометрических задачах способствует реализации
внутрипредметных связей школьных курсов алгебры и геометрии и является
выигрышным для восприятия.
Литература:
1. Азаров А.И. Системы
алгебраических уравнений. Текстовые задачи [Текст]: учебное пособие/А.И.
Азаров-Мн,1998. - 288 с.
2. Нагорнов О.В. Сборник
задач по алгебре. Часть 2. Иррациональные, тригонометрические, логарифмические
уравнения и неравенства. Прогрессии. В помощь учащимся 10–11 классов [Текст]:
учебное пособие/ О.В.Нагорнов, А.В. Баскаков–М.: НИЯУ МИФИ, 2009.-160 с.
3. Сканави М.И. Сборник задач по математике для поступающих во
втузы, [Текст]:учебное пособие/М.И.Сканави, В.К.Егерев.–М.:ООО Издательство
«Мир и образование»: ООО «Издательство ОНИКС-ЛИТ»,2013.–608 с.