Никишина Н.А.

Лесосибирский педагогический институт – филиал СФУ, Лесосибирск

Решение софизмов на клетчатой бумаге с использованием программы «Живая геометрия»

Одним из средств повышения интереса к математике служит использование в обучении различных парадоксов и софизмов [1, с 13].

Геометрические софизмы – это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или противоречивое утверждение, связанное с геометрическими фигурами и действиями над ними. В планиметрии большая часть ошибочных доказательств связана с использованием неправильных чертежей.

Рассмотрим, например, удивительное «доказательство» того, что площадь лицевой стороны многоугольника, вырезанного из бумаги, отличается от площади оборотной стороны того же многоугольника. Это «доказательство» придумано врачом-психиатром Л. Восбургом Лионсом.

Если начертить на листке бумаги в клетку фигуру, названную «треугольником Керри» в честь её первооткрывателя (рис.1), и разрезать её вдоль прямых, то перевернув части фигуры на другую сторону и составив из них фигуру, изображенную на рис. 2, мы обнаружим, что в центре новой фигуры появилась дырка площадью в 2 клетки. Иначе говоря, суммарная площадь частей исходной фигуры при переворачивании уменьшилась до 58 клеток! Перевернув еще раз (лицевой стороной вверх) лишь три части исходной фигуры, мы сможем составить из всех шести частей фигуру, изображенную на рис. 3. Её площадь равна 59 клеткам.

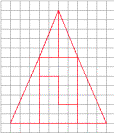
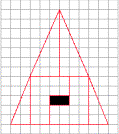
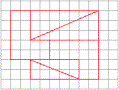
Рис. 1 Рис. 2 Рис. 3

Ошибка становится более очевидной, если использовать программу Живая Геометрия. Здесь уже свои гипотезы учащиеся могут проверить или опровергнуть, проведя непосредственно необходимые линии и сделать выводы.

Если мы соединим точки А и В на первом чертеже, то увидим, что отрезки, которые мы считали сторонами треугольника оказались не прямыми, а ломаными линиями (рис. 4).

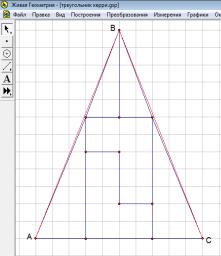
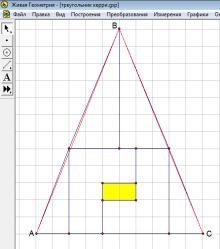
Рис. 4 Рис. 5

То же самое наблюдаем и на втором чертеже (рис. 5). И тогда возникает вопрос: чему же все-таки равна площадь этих фигур? Обратив внимание на последний чертеж (рис. 6), можно увидеть, что все его отрезки прямолинейны, никаких зазоров между линиями нет, следовательно, площадь всех этих фигур равна 58 клеткам независимо от перестановок.

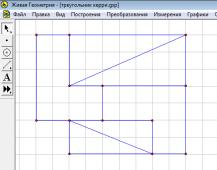
Рис. 6

Одно из главных достоинств "Живой геометрии" - возможность изменять объекты и перемещать их. Это преимущество можно использовать при изучении софизмов для наглядности. По мере приобретения навыков работы с программой деятельность учащегося развивается по таким направлениям, как анализ, исследование, построение, доказательство, решение задач, а также решение головоломок и даже рисование.

Таким образом, благодаря клетчатой бумаге и возможностям программы "Живая геометрия", мы уверенно можем сопровождать стандартный материал школьной программы и выходить за её пределы, иллюстрировать уже известные факты геометрии и предполагать открытие новых, проводить эксперименты и развивать навыки проведения доказательных рассуждений.

Литература:

1. Гайдук, Ю.М. Математические софизмы [Текст] / Ю.М. Гайдук // Математика в школе. – 1952. – № 6. – С. 13 – 18

2. Гарднер, М. Математические чудеса и тайны [Текст] / М. Гарднер. – М.: Наука, 1964.

3. Линдгрен, Г. Занимательные задачи на разрезание. Пер. с англ. Ю.Н. Сударева. Под ред. и с послесл. И.М. Яглома. – М.: «Мир», 1977.

4. Шарыгин, И.Ф. Наглядная геометрия [Текст] / И.Ф Шарыгин, Л.Н. Ерганжиева // Учебное пособие для учащихся V—VI классов. – 1995.

5. Сайт учителя математики Фефеловой Виктории Режим доступа: http://fefelova.ucoz.ru/index/zhivaja_geometrija/0-29