И.А. Долгарев, А.И. Долгарев
К СОВРЕМЕННМУ CОCТОЯНИЮ ТЕОРИИ ПОВЕРХНОСТЕЙ
В работе приведена схема изложения начал евклидовой теории поверхностей в связи с выражением коэффициентов формы кривизны (второй квадратичной) через коэффициенты метрической формы поверхности, [1]. Выявляются некоторые дополнительные свойства регулярных поверхностей, [2,3]. Это влечет изменения в изложении теории поверхностей. Важным является содержание внутренней геометрии поверхности и отношение к изометричным поверхностям. Наметим схему изложения фактов с акцентом на фундаментальные дифференциальные формы поверхностей.
Предполагается, что начальные понятия евклидовой дифференциальной геометрии вводятся традиционно. Считается обязательным изложение следующих тем.
Основные понятия теории кривых.
Регулярная кривая. Сопровождающий репер кривой. Кривизна и кручение кривой, вычисление в произвольной параметризации. Натуральные уравнения кривой. Поведение кривой вблизи обыкновенной точки.
Первые понятия теории поверхностей.
Определение поверхности, регулярная поверхность. Задание поверхности векторной функцией
= 
, 
. (1)
Касательная плоскость и нормаль поверхности в обыкновенной точке. Нормальная кривизна линий на поверхности. Фундаментальные формы поверхности: метрическая форма и форма кривизны. Вычисление коэффициентов фундаментальных форм. Индикатриса кривизны. Главные кривизны, полная и средняя кривизны поверхности. Классификация обыкновенных точек поверхности.
Основное значение имеет определяемость регулярной евклидовой поверхности ее метрической формой. Этому вопросу в настоящей работе уделено большое внимание. Более 150 лет назад была доказана определяемость поверхности коэффициентами первой и второй квадратичных форм – теорема Петерсона-Бонне. В настоящее время коэффициенты второй формы оказались выраженными через коэффициенты первой формы. Указанный факт влияет на содержание теории поверхностей.
1. Выражение коэффициентов формы кривизны
через коэффициенты метрической формы поверхности
Регулярная евклидова поверхность в общем случае описывается функцией (1) и может быть задана в окрестности всякой своей обыкновенной точки явной функцией, см. например, [4, c. 210 – 213],
,
иными словами это поверхность-график, или явно заданная поверхность. Векторная функция, описывающая поверхность, такова:
= 
, 
. (2)
Как и в случае (1), поверхность является 2-параметрической. Коэффициенты
метрической формы 
поверхности в
параметризации (2) равны
, 
, 
; 
= 
. (3)
Коэффициенты формы кривизны 
поверхности (2) есть
, 
, 
. (4)
1.
ТЕОРЕМА. [1] Коэффициенты
формы кривизны 
евклидовой регулярной поверхности (2) выражаются через
коэффициенты метрической формы 
следующими формулами
, 
, 
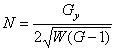. (5)
# По (3) имеем 
. Дифференцируем первую и третью формулы из (3):
, 
, 
, 
.
(6)
Отсюда находим:
= 
, 
, 
, 
. (7)
Первые
две формулы подставляем в соответствующие формулы в (4) и получаем первую и
третью формулы в (5). Перемножаем значения производных 
в (7), получаем с
использованием второй формулы из (3):
,
а отсюда имеем вторую формулу в (5). #
Теорема 1 может быть сформулирована в виде
2. ТЕОРЕМА. Коэффициенты формы кривизны 
евклидовой регулярной поверхности являются функциями коэффициентов
метрической формы 
и их производных первого порядка. #
Вместе с тем справедливо
3. УТВЕРЖДЕНИЕ. Справедливо неравенство
.
(8)
4. СЛЕДСТВИЕ. Знаки величин 
и 
одинаковы. #
2. Следствия
выражения коэффициентов формы кривизны поверхности
через коэффициенты
метрической формы
Подставляя формулы (5) в известные формулы теории поверхностей, приходим к некоторым следствиям.
5. ТЕОРЕМА. [1, теорема 1]
Для явно заданной поверхности 
полная кривизна выражается через коэффициенты ее метрической формы и
производные первого порядка этих коэффициентов и имеет вид
. (9)
Согласно [3], средняя кривизна поверхности равна
.
Нормальная кривизна линий на поверхности такова:
, 
.
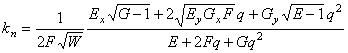Как известно, полная кривизна поверхности равна
.
Вид обыкновенной точки поверхности определяется знаком полной кривизны поверхности в этой точке. По формуле (9) и утверждению 3, справедлива
6. ТЕОРЕМА. [3, теорема 7] Обыкновенная
точка евклидовой регулярной поверхности является эллиптической, если в этой
точке величины
и 
отличны
от нуля и имеют одинаковые знаки; является гиперболической, если указанные
величины отличны от нуля и имеют противоположные знаки; и точка является параболической
или точкой уплощения, если
.
3. О внутренней
геометрии поверхности
Предмет внутренней геометрии поверхности принято связывать с метрической (первой квадратичной) формой поверхности. Согласно [4, c. 225], «Те геометрические свойства поверхности, которые можно установить, исходя из задания только первой квадратичной формы, относятся к внутренней геометрии поверхности.» Вместе с тем отмечается, что внутренняя геометрия поверхностей изучает изгибание поверхностей. Известны теоремы Либмана и Гильберта: первая о неизгибаемости сферы, вторая – о несуществовании в 3-мерном евклидовом пространстве полной регулярной поверхности отрицательной кривизны, т.е. о неизгибаемости поверхности отрицательной кривизны на плоскость. В связи с фактом выражения коэффициентов формы кривизны поверхности через коэффициенты метрической формы, теорема 1, лучше внутреннюю геометрию поверхности связывать только с изгибанием поверхности.
4. Определяемость
поверхности метрической формой
Схема отыскания поверхности по ее метрической форме содержится в [2, 5].
7. ТЕОРЕМА. Если на
односвязной области 
евклидовой плоскости заданы действительные дифференцируемые функции
двух действительных аргументов
, (10)
удовлетворяющие условиям
, (11)
то на этой области определяется поверхность (2) с точностью до положения в пространстве, для которой функции (10) являются коэффициентами метрической квадратичной формы. Начальные условия
,
выделяют единственную поверхность,
проходящую через точку 
и имеющую в этой точке касательную плоскость
, где 
, 
. (12)
# Первое из условий (11) означает, что имеется дифференциальное уравнение в полных дифференциалах
. (13)
Решение уравнения существует, обозначим его
, 
. (14)
Согласно
(3), первая квадратичная форма каждой из поверхностей (14) имеет коэффициенты
(10). Действительно, по заданным уравнениям имеем 
, 
и по условию теоремы 
. Формулы (3) означают 
, 
. Заданные начальные условия из семейства (14) выделяют
единственную поверхность с касательной плоскостью (12). #
В формулах 
, полученных из формул (3), значения радикалов имеют два знака
, т.е.
, 
.
8. ЛЕММА. Знаки перед
радикалами определяются по второму коэффициенту 
метрической формы поверхности, см. (3); при 
в обыкновенной точке 
в области 
определения функции 
знаки производных 
одинаковы, при 
знаки производных противоположны. #
Возможны следующие векторы, определяющие касательную
плоскость в точке 
поверхности (2):
, 
,
где 
, 
. Плоскости 
, 
и также плоскости 
, 
симметричны
относительно плоскости 
, т.е. определены с точностью до положения в пространстве.
Знаки рассматриваемых радикалов могут быть получены и по начальным условиям, где задана точка, через которую поверхность проходит.
Тем самым и поверхность (2) определяется с точностью до положения.
5. Пример получения поверхности по метрической форме
Эллиптический и гиперболический параболоиды задаются функцией
.
Имеем 
; коэффициенты метрической формы поверхностей есть
. (15)
Теперь,
считая функции (15) заданными, отыскиваем функцию 
, описывающую поверхность. Согласно (3), 
, 
. По (15) находим
.
По
коэффициенту 
видно, что обе
производные 
имеют знаки, либо
совпадающие со знаками координат 
обыкновенной точки,
либо противоположны этим знакам. Сначала
рассмотрим случай 
и пусть
.
В соответствии с теоремой 7, уравнение (13) принимает вид
.
Его решение есть
.
Условие
выделяет
эллиптический параболоид 
.
Далее, рассмотрим случай 
, и пусть
, 
.
Имеется дифференциальное уравнение
,
см.
(13), оно определяет гиперболический параболоид 
.
В случаях 
и 
определяются те же
поверхности, но
симметричные полученным, т.е. поверхности получены с точностью до положения в пространстве.
6. Связь с
изометричностью поверхностей
Существование изометричных поверхностей, на первый взгляд, вызывает некоторые сомнения в определяемости поверхности метрической формой.
Известно, что существуют изометричные поверхности, не совпадающие в движениях, например, плоскость и цилиндр. Кажется, что предлагаемая работа заведомо противоречива, знакомиться с такой работой не хочется. Но дело в том, что речь идет о различных вещах. Для каждой из различных изометричных поверхностей указывается своя параметризация, с тем, чтобы метрические формы поверхностей совпадали. Авторы работы для всех поверхностей рассматриваю одну и ту же параметризацию, чтобы каждая поверхность в этой общей параметризации задавалась своей функцией, и по метрической форме поверхности восстанавливают поверхность.
Изометричные поверхности, не
совпадающие в результате евклидовых движений, описываются различными функциями
(2). Участок 
плоскости 
при 
, 
описывается функцией 
или векторной
функцией
.
(Векторы евклидова пространства 3-мерны.) При этом
, 
.
Цилиндрическая
поверхность 
описывается функцией 
, или на области 
функциями 
. Выберем 
. Изменим обозначения:
рассматривается цилиндр 
в виде
.
В параметризации 
цилиндр обладает
метрической функцией с коэффициентами 
, как и плоскость 
.
Функции 
и 
на области 
различны, задают
различные поверхности, хотя и изометричные; цилиндр не получается из плоскости
евклидовым движением, но получается изгибанием.
Для цилиндра имеем
, 
.
Метрические
формы плоскости 
и цилиндра 
различны. Естественно
ожидать, что они определяют различные поверхности.
Для отыскания поверхности по
коэффициентам 
в окрестности точки 
,согласно (13), получается дифференциальное уравнение
,
для
отыскания поверхности по коэффициентам 
в окрестности точки 
получается
дифференциальное уравнение
.
Имеется
в первом случае плоскость 
, во втором случае –
цилиндр 
. Задача нахождения поверхности по ее метрической функции
разрешилась и однозначно с точностью до движения пространства.
Задача определяемости регулярной евклидовой поверхности 3-мерного пространства ее метрической формой разрешена полностью: не только установлена такая определяемость, но и указан способ получения поверхности по заданным коэффициентам метрической формы. Разрешена задача элементарными средствами, может излагаться в учебных курсах, см. [5].
Список литературы
- Долгарев А.И. Новый вид основной теоремы Гаусса в евклидовой теории поверхностей. // Materiali IX mezinarodni vedecko-praktika conference «Dni vedy – 2013» - Dil 32. Matematika. Vystavba a architektura: Praga. Publiching House “Education and Skience”. s.r.o. – 2013. С. 55 – 60.
- Долгарев А.И. Система линейных уравнений первого порядка в частных производных. Задание евклидовой поверхности коэффициентами ее первой квадратичной формы. // Materiali IX mezinarodni vedecko-praktika conference «Dni vediy – 2013» - Dil 32. Matematika. Vystavba a architektura: Praga. Publiching House “Education and Skience”. s.r.o. – 2013. С. 32 – 40.
- Долгарев А.И. Добавочные возможности
первой квадратичной формы евклидовой поверхности. // Materialy IX Miedzynarodowej naukowi-praktycznej konferencji
“Dinamika naukowych badan
– 2013” Volume 12.
Matematyka. Fizyka.
Nowoczesne informacyjne technologie. Chemia i chemiczne technologie: Przemysl.
Nauka i studia – 2013, C. 20 – 26.
- Рашевский П.К. Курс
дифференциальной геометрии. – М.: Гостехиздат, 1956. 420с.
5. Долгарев И.А., Долгарев А.И. Обновленная основная теорема теории поверхностей
в курсе геометрии. // Информационные технологии в математике и математическом
образовании. Материалы II Всероссийской научно-методической конференции.
Красноярск: КГПУ – 2013, С. 327 – 331.