Таттибеков К.С.
Таразский государственный педагогический институт, Казахстан
Высшие симметрии OSP(2/1)
- нелинейное уравнение Шредингера
При
групповом анализе произвольная эволюционная система
![]() (1)
(1)
и ее различные
дифференциальные следствия рассматриваются как бесконечномерное многообразие
[F] в пространстве переменных
![]()
Условие
инвариантности многообразия [F] по отношению группы преобразований записывается
в виде определяющего уравнения [1]
![]() (2)
(2)
где ![]() -операторы полного
дифференцирования по t и x соответственно,
-операторы полного
дифференцирования по t и x соответственно, ![]() - вычисляется с
помощью уравнений (1). Решения определяющего уравнения (2) образуют алгебру
Ли-Бэклунда допускаемой системой (1).
- вычисляется с
помощью уравнений (1). Решения определяющего уравнения (2) образуют алгебру
Ли-Бэклунда допускаемой системой (1).
Один из
способов интегрирования связан с вычислением алгебры Ли-Бэклунда, включающий в
себя множество высших симметрий уравнения. Этот подход позволяет
систематический находит частные решения, причем высшие симметрии связаны с
решениями солитонного типа [1,2]. В этой работе построены группы симметрии
уравнений OSP(2/1)-S3.
Так в
работах [3,4] были построены ![]() - градуированное суперобобщение нелинейного уравнения
Шредингера OSP(2/1) - S3:
- градуированное суперобобщение нелинейного уравнения
Шредингера OSP(2/1) - S3:
![]()
![]() (3)
(3)
![]()
![]()
где ![]() - функция четности,
т.е
- функция четности,
т.е ![]() - коммутирующие,
- коммутирующие, ![]() - антикоммутирующие
искомые функции.
- антикоммутирующие
искомые функции.
Система
уравнений (3) является условием совместности линейной системы
![]()
![]()
![]()
![]() .
.
Здесь -![]() где
где ![]() - генераторы супергруппы OSP(2/1):
- генераторы супергруппы OSP(2/1):
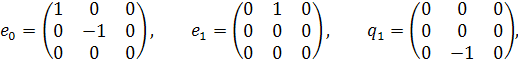
![]() удовлетворяющие
коммутационным соотношениям
удовлетворяющие
коммутационным соотношениям
![]()
![]()
![]()
где st-операция супертранспонирования, [,]-коммутатор, {,}-
антикоммутатор.
Непосредственной
проверкой нетрудно установить следующие равенства
![]()
где Н = ![]() –
ортосимплектическая матрица супергруппы
–
ортосимплектическая матрица супергруппы
OSP(2/1), ![]()
Система
уравнений OSP(2/1)-S3 (3) как интегрируемое
уравнение обладает N -
солитонным решением, бесконечным числом интегралов движения и т.д.
Пусть
функции ![]() исчезают при
исчезают при ![]() . Тогда плотность
. Тогда плотность ![]() локальных интегралов
движения
локальных интегралов
движения
![]()
определяется по рекуррентным формулам
![]()
где ![]() ,
,
![]()
![]()
Первые несколько интегралов
сохранения
![]()
![]()
Определяющие
уравнения для операторов Ли-Бэклунда
![]()
допускаемой системой
OSP(2/1)-S3 (1) имеет вид (4):
![]()
![]()
![]()
![]()
Решение
определяющего уравнения (2) вида ![]() назовем решением m - порядка и обозначим через
назовем решением m - порядка и обозначим через ![]() . Мы будем рассматривать решение определяющих уравнений (4) явно независящих от х,t.
. Мы будем рассматривать решение определяющих уравнений (4) явно независящих от х,t.
ЛЕММА. Решение порядка m уравнений (4) имеет вид
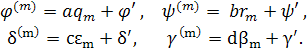 (5)
(5)
где а, b, с, d - постоянные числа, функций ![]() - зависят от
- зависят от ![]()
Доказательство. Подстановка функций ![]() зависящих от
зависящих от ![]() и их производных по х до m - го порядка включительно в первое уравнение (4) дает (6):
и их производных по х до m - го порядка включительно в первое уравнение (4) дает (6):
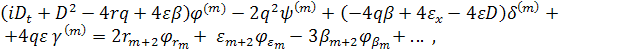
где многоточием отмечены
слагаемые меньшего порядка. Отсюда следует, что должно быть
![]() (7)
(7)
С учетом последнего,
уравнение (6) перепишется так
![]() +
+ ![]()
Следовательно, ![]() (8)
(8)
Тогда, из (7),(8) следует справедливость
первого равенства в (5).
Аналогично
поступая со всеми остальными определяющими уравнениями (4), окончательно
убеждаемся в справедливости леммы.
Используя
указанную в доказательстве леммы схему найдем решения определяющих уравнений
первых нескольких порядков;
![]()
![]()
![]()
![]()
![]()
![]() и т.д.
и т.д.
Нетрудно
показать, что по шаговое уточнение алгебры (5) для любого m приведет к справедливости следующих равенств
![]()
![]()
где многоточием отмечены
слагаемые меньшего порядка, представляющие собой сумму однородных многочленов
относительно ![]() и их производных по х до порядка
и их производных по х до порядка ![]()
ТЕОРЕМА.
Алгебра Ли - Бэклунда системы нелинейных уравнений OSP(2/1)-S3 коммутативна, ее
элементы порядка ![]() вычисляются по
рекурентным формулам (9):
вычисляются по
рекурентным формулам (9):
![]()
![]()
![]() +
+
![]()
![]() -
-
![]()
![]() причем
причем ![]()
Доказательство.
Сначала покажем, что оператор ![]() в (9) имеет смысл,
т.е.
в (9) имеет смысл,
т.е.
![]()
где ![]() - некоторая
дифференциальная функция .
- некоторая
дифференциальная функция .
Для семейства
![]()
уравнений OSP(2/1)-S3
имеем, что
![]()
где ![]() означает производную
по времени соответствующей потоку k.
С другой стороны знаем, что
означает производную
по времени соответствующей потоку k.
С другой стороны знаем, что ![]() - плотность закона
сохранения, следовательно
- плотность закона
сохранения, следовательно ![]() т.е. выражение
т.е. выражение ![]() является полной производной.
является полной производной.
Далее подстановка
(9) в
(4) дает
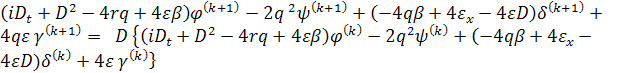
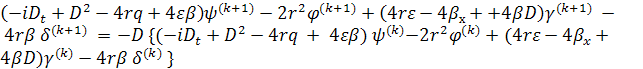
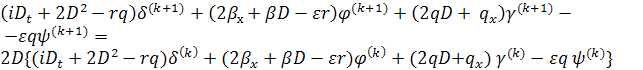
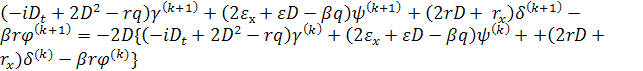 ,
,
из которых следует справедливость рекурентных
формул (9).
Умножение в алгебре
Ли-Бэклунда определим по формуле
![]()
где ![]() - функция четности. Тогда доказательство коммутативности
построенной алгебры сводится к установлению следующих равенств
- функция четности. Тогда доказательство коммутативности
построенной алгебры сводится к установлению следующих равенств
![]()
![]()
для операторов Ли-Бэклунда
![]()
Справедливость
последних равенств устанавливается непосредственной проверкой.
Отметим, что в бозонном
случае ![]() полное описание
алгебры Ли-Бэклунда проведено в [5].
полное описание
алгебры Ли-Бэклунда проведено в [5].
Литература:
1. GurseesM., Qquz O. A super Soliton Connection /Lett.Math.Phys., 1986,
v.11, №3, p.235-246.
2. Жибер А.В. Уравнения
n - волн и система нелинейных уравнений Шредингера /ТМФ, 1982, т.52, №3,
с.405-413.
3. Ибрагимов Н.Х. Группы
преобразований в математической физике. М.:Наука, 1983.
4. Kulish P.P. Quantum OSP-invariant nonlinear Schrodinger еquations
/Lett. Math. Phys.,1985, v.10, p.87-93.
5. Олвер П. Приложение
групп Ли к дифференциальным уравнениям. Пер.с англ. -М.:Мир, 1989, -639 с.