МОДЕЛИРОВАНИЕ ГИДРОДИНАМИЧЕСКИХ ПОТОКОВ В КОЛОННОМ АППАРАТЕ

Кажгалиев К.С.

Евразийский национальный университет имени Л.Н. Гумилева, г. Астана kairbek.ks@mail.ru

АННОТАЦИЯ

При моделировании процессов химической технологии одним из главных факторов является гидродинамика потоков в аппаратах. Структура потоков оказывает существенное влияние на эффективность химико-технологических процессов, поэтому ее необходимо учитывать при моделировании. В данной работе был разработан программный продукт, в основе которого лежит универсальная математическая модель, описывающая гидродинамику реальных потоков - модифицированная ячеечная модель, которая может учитывать сложности, возникающие в различных аппаратах при оценке существование обратных потоков в аппарате. Программный продукт разработан в среде Delphi 7.

ANNOTATION

When modeling the processes of chemical technology one of the main factors is the hydrodynamics of flow in the apparatus. Flow structure has a significant impact on the efficiency of chemical processes, so it must be taken into account in the simulation. In this paper programme model was developed which is based on a universal mathematical model describing the hydrodynamics of real flows - modified cell model that can take into account the complexities involved in a variety of devices in assessing the existence of reverse flows in the machine. Programme model is developed in Delphi 7.

В настоящее время в химической промышленности начинают широко применять компьютерное моделирование для оптимизации старых и создания новых производств. Разработанную математическую модель процесса необходимо использовать для исследования и прогнозирования поведения реального объекта, т.е. её свойства и поведение с определённой степенью приближения должны совпадать с моделируемым процессом. Это свойство математической модели называется свойством традуктивности, или переносимости результатов расчёта, получаемых с помощью математической модели, на поведение реальных химико-технологических процессов. В результате вместо анализа свойств реальных объектов или их физических моделей, реализуемых обычно на пилотных или полупромышленных установках, большинство исследований можно проводить с применением разработанной математической модели, что существенно дешевле, быстрее и безопаснее. Для корректного решения этих задач необходимо, чтобы математическая модель была адекватна реальному процессу.

В данной работе представлена математическая модель гидродинамики на макроуровне. Выбор модели, адекватно описывающий гидродинамику потока в аппарате с помощью разработанного программного продукта, выполнялся на насадочном абсорбере. Абсорбцией называется процесс поглощения газа или пара жидким поглотителем (абсорбентом). В промышленности абсорбция с последующей десорбцией широко применяется для выделения из газовых смесей ценных компонентов (например, для извлечения из коксового газа аммиака, бензола и др.), для очистки технологических и горючих газов от вредных примесей (например, для очистки отходящих газов от сернистого ангидрида) и т.д. При абсорбции процесс массопередачи протекает на поверхности соприкосновения фаз. Поэтому в аппаратах для поглощения газов жидкостями (абсорберах) должна быть создана развитая поверхность соприкосновения между газом и жидкостью. Скорость массопередачи в насадочном абсорбере зависит от гидродинамического режима в аппарате.

Насадочные абсорберы представляют собой колонны, загруженные насадкой – твердыми телами различной формы – для увеличения поверхности соприкосновения между газом и жидкостью. Жидкость стекает по поверхности насадки тонкой пленкой и одновременно распределяется в слое насадки в виде капель и брызг. Насадка опирается на решетку, в которой имеются отверстия для прохода газа и стока жидкости. Газ поступает в колонну снизу и движется вверх противотоком по отношению к жидкости.

В целях данной работы компьютерное моделирование гидродинамики потоков в аппаратах осуществлялось в среде Delphi на языке Object Pascal. Для оценки адекватности различных моделей использовалась сумма квадратов отклонений, полученных при моделировании, от соответствующих значений на экспериментальной кривой разгона.

Решение систем дифференциальных моделей производилось с помощью численного метода Эйлера. Использовались следующие параметры аппарата: внутренняя S поперечного сечения, высота аппарата, объемная скорость потока в аппарате, внутренние характеристики аппарата по наличию обратных потоков и продольной диффузии. Экспериментальная кривая разгона, т.е отклик аппарата на ступенчатом возмущение приведена в таблице 1.

Таблица 1 - Кривая разгона аппарата ( Cо=0,18):

Время, с	1	2	3	4	5	6	7	8	9	10
Концентр., % об.	0,001	0,008	0,01	0,027	0,045	0,075	0,1	0,12	0,14	0,16

При запуске программы открывается диалоговое окно выбора режима работы. Разработан следующий режим расчета аппарата (рис.1).

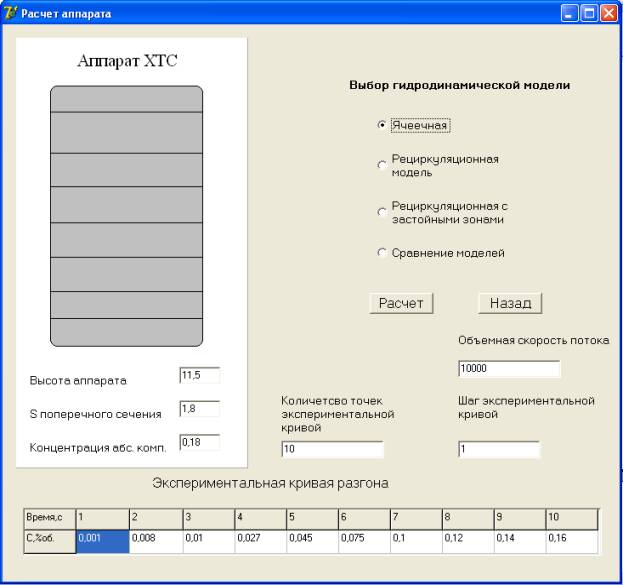
Рисунок 1. Окно расчета аппарата.

В данном окне предлагается ввести данные по экспериментальной кривой разгона химического аппарата, т.е. отклик аппарата на ступенчатое возмущение (на вход в аппарат подается индикатор с известной концентрацией, на выходе из аппарата фиксируется выходное значение концентрации через определенное время). Далее вносятся объемная скорость потока, проходящего через аппарат, а также высота и площадь поперечного сечения аппарата и выбирается модель.

Предлагается использовать ячеечную модель для тарельчатых колонн (для разделения бензиновых фракций, газового конденсата), аппаратов с псевдожиженным слоем, насадочных колонн. Далее для проведения расчетов необходимо ввести дополнительные параметры (рис. 2). В данном окне выбирается шаг метода Эйлера при решении системы дифференциальных уравнений.

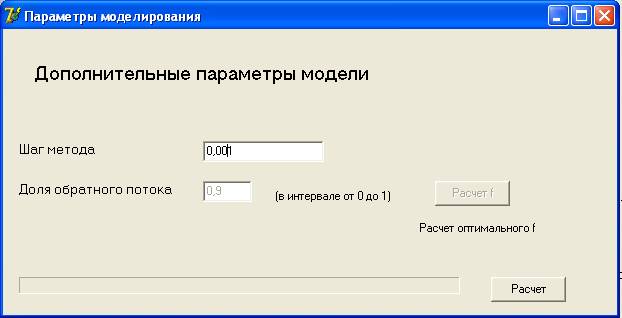Рисунок 2. Окно дополнительных параметров ячеечной модели

Результаты ячеечной модели для данного аппарата показали хорошее совпадение с экспериментальными данными вполне адекватные результаты со среднеквадратичной погрешностью 0,0000000614990401. Наиболее адекватно описывает гидродинамику данного аппарата ячеечная модель с 5 ячейками (рис 3).

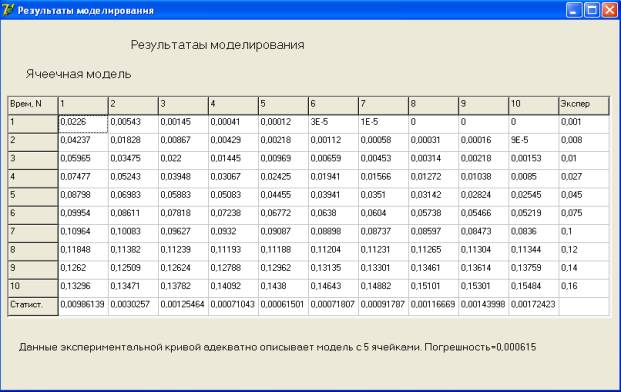
Рисунок 3. Окно вывода результатов и рекомендаций

В заключение, данная компьютерная модель может быть использована для выявления структуры и поведения потока в аппарате, моделирования новых и оптимизации уже действующих аппаратов химической технологии. В возможна программная реализация модели с застойными зонами, которая позволит повысить точность результатов, а также расширит возможность для расчета химико-технологических процессов.

Список использованной литературы:

1. Кафаров В.В., Глебов М.Б. Математическое моделирование основных процессов химических производств. –М.: Высш. шк., 1991. – 400 с.

2. Закгейм А.Ю. Введение в моделирование химико-технологических процессов.- М.:Химия , 1982.

3. Кроу К. Математическое моделирование химических процессов М.:Мир, 1973.