Технические науки/12. Автоматизированные системы управления на производстве

Д.т.н. Бурмистрова О.Н.¹, Сушков А.С.², Бурмистров В.А.¹

ФГБОУ ВПО «Ухтинский государственный технический университет», ФГБОУ ВПО «Воронежская государственная лесотехническая академия»

Обоснование положения генетического подхода для решения задач многокритериальной оптимизации

В статье приведены результаты экспериментов по оценке эффективности многоточечности и полигамности, составляющими основу предложенного смешанного эволюционного метода, в сравнении с известными генетическими методами.

Ключевые слова: генетический алгоритм, эволюционные методы, тестовые задачи, оценка качества

Генетические алгоритмы (ГА) выражают эволюцию популяции хромосом в направлении от начального поколения к окрестностям экстремума. Обоснование этого положения содержится в основной теореме генетического подхода – теореме схем (иначе называемой schemata theorem или теорема шаблонов) [1].

Ранее в работах [2, 3] рассматривался разработанный автором гибридный модифицированный эволюционный алгоритм и перспективы его применения для решения задач многокритериальной оптимизации. В этой статье приведены результаты экспериментов по оценке эффективности многоточечности и полигамности, составляющими основу предложенного смешанного эволюционного метода, в сравнении с известными генетическими методами. Для исследования эффективности ГА предложено несколько вариантов тестовых функций. Известен набор тестовых функций К. ДеДжонга, в котором имеются одно- и многоэкстремальные функции с различным рельефом, а также ряд других наборов [4].

К числу основных тестовых задач для проверки отдельных аспектов эффективности разрабатываемых методов относятся задачи маршрутизации транспортных средств с временными окнами, задача двумерной упаковки, задача синтеза топологии и распределения трафика в вычислительных сетях и др.

Большинство предложенных наборов включает задачи непрерывной оптимизации сравнительно малого размера. Одной из основных тестовых задач отражающих особенности задач пространственно-временного синтеза, является задача синтеза расписаний – JSSP (Job Shop Scheduling Problem) [1, 4].

К исходным данным задачич JSSP относятся:

Q – число стадий обслуживания каждой работы;

А = {A₁,A₂,...A_n} – множество работ;

M ={M₁,M₂,...M_m} – множество исполнителей (машин, единиц техники и т.п.);

P = [P_ij] – матрица производительностей машин, где P_ij – затраты времени на выполнение работы i на машине j;

C= (C₁,C₂,...C_m) – вектор цен, где C_j – цена за единицу времени работы машины M_j;

T = (T₁,T₂,...T_n) – ограничения на время окончания работ, где T_i – предельное время для завершения работы i;

Q – штраф, добавляемый к общим затратам Z при нарушении какой-либо работой соответствующего ей временного ограничения.

Требуется составить расписание, при котором минимизируются затраты на выполнение всех работ с учетом штрафов.

Приведены результаты экспериментов по оценке эффективности многоточечности и полигамности, составляющими основу предложенного гибридного эволюционного алгоритма, в сравнении с известными генетическими методами. В качестве тестовой примем задачу JSSP. Для сравнительного анализа результатов тестирования кроме разработанного алгоритма (ГМЭА) примем к рассмотрению следующие методы: CGA (Classic Genetic Algorithm), HCM (Heuristics Combination Method), PSO (поведение толпы), ASO(колония муравьев), VEGA (Vector Evaluated Genetic Algorithm), FFGA (Fonseca and Fleming’s Multiobjective Genetic Algorithm), NPGA (Niched Pareto Genetic Algorithm), SPEA (Strength Pareto Evolutionary Algorithm).

Выполненное исследование потенциала рекомбинации позволяет сделать вывод о наличии оптимальных значений длин фрагментов L, на которые разделяются хромосомы при кроссовере. Для подтверждения этого вывода было проведено экспериментальное исследование зависимости функций полезности от L на примере задачи JSSP.

Ранее отмечено, что снижение эффективности генетического поиска происходит из-за явления преждевременной стагнации. Это явление исследовалось на применении методов HCM и предложенного гибридного алгоритма к задаче синтеза расписаний со следующими исходными данными: число стадий обслуживания работ q=4 стадии, число работ n=105, число машин m=15. Результаты двух вариантов решения задачи при применении каждого из сравниваемых методов приведены в табл. 1, где N – число разрывов хромосом при кроссовере (отметим, что длина хромосомы в данной задаче равна =420), Evals– число оценок целевой функции.

Таблица 1 – Решение задачи JSSP

Evals	270	20т	30т	40т	50т	75т	100т	125т
N=20	22570	22293	22121	21963	21901	21834	21821	21811
N=20	23498	22147	22073	21970	21850	21798	21789	21781
N=1	22570	22145	22126	22118	22118	22118	22118	22118
N=1	23498	22134	22119	22100	22099	22083	22072	22072

Результаты показывают, что при многоточечном кроссовере вероятность преждевременной стагнации уменьшается, соответственно удается заметно ближе подойти к точке экстремума.

На рисунке 1 представлена зависимость коэффициента разнообразия генов r (доля генов, имеющих неодинаковые значения в хромосомах родителей в очередном акте кроссовера) от номера поколения.

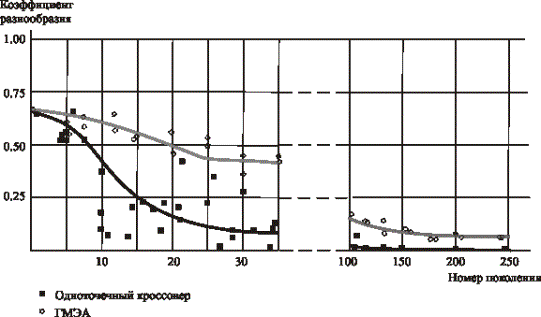
Рис. 1 Иллюстрация вырождения популяции с ростом числа поколений

На рисунке светлыми точками обозначены значения r, полученные в некоторых случайно выбранных актах кроссовера при применении разработанного метода, а темными точками – аналогичные значения, полученные при применении одноточечного кроссовера (СGA). Рисунок иллюстрирует заметно меньшую предрасположенность разработанного алгоритма к ранней стагнации.

В [5] приводится теоретическое обоснование наличия оптимальных значений длин фрагментов L в смешанном эволюционном методе. Для подтверждения теоретических результатов были проведены эксперименты по определению оптимальных значений L.

На рис. 2 представлены результаты решения задачи синтеза многостадийных расписаний с 4 стадиями, 200 работами и 15 машинами с помощью разработанного метода. Точки соответствуют отдельным вариантам решения, кривая отображает усредненную зависимость целевой функции от размера фрагмента L.

Полученные результаты позволяют сделать вывод: длина фрагментов L влияет на эффективность поиска. Для разработанного алгоритма в задаче JSSP оптимальные значения L находятся в диапазоне {5, 40} при общей длине хромосомы, равной 800. Следовательно, однородный и одноточечный кроссоверы не относятся к лучшим вариантам ГА.

Аналогичные результаты были получены при решении других тестовых задач. Рис. 2 иллюстрирует результаты решения задачи маршрутизации транспортных средств с временными окнами (VRPTW), в которой хромосомы содержат по 40 генов, а рис. 3 – результаты решения задачи синтеза топологии и распределения трафика (СТРТ) в вычислительной сети с хромосомами длиной в 276 генов. В обоих случаях использовался метод ГМЭА.

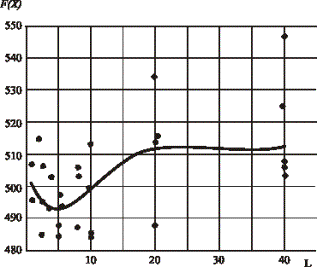
Рис. 2 Зависимость результатов решения задачи VRPTW от длины фрагментов L

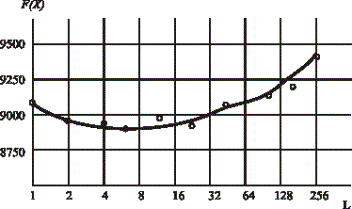
Рис. 3 Зависимость результатов решения задачи СТРТ от длины фрагментов L

Интерес представляет сравнение разработанного ГМЭА с методами PSO и ACO [6]. Результаты такого сравнения приведены на рис. 4, где Delta есть разность между полученным и наилучшим известным результатом решения тестовой задачи синтеза многостадийных расписаний с 105 работами. Эти результаты свидетельствуют о преимуществе разработанного метода перед другими сравниваемыми методами.

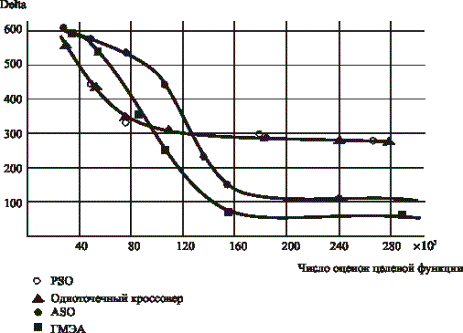
Рис. 4 Сравнение результатов решения задачи синтеза расписаний различными генетическими методами

Оценка эффективности разработанного алгоритма проводилась на примере следующей разновидности тестовой задачи синтеза расписаний JSSP: задано:

1) Множество работ A={A₁, A₂,…,A_n}, где каждая работа A_i последовательно проходит q стадий обслуживания;

2) На каждой стадии имеется m_k машин , общее число машин ;

3) Для обслуживания работы А_i на стадии k, выбирается одна из m_k машин;

4) Одновременно на одной машине может обслуживаться не более одной работы, начатое обслуживание не прерывается;

5) Все работы распределены по типам и, если соседние во времени исполнения работы, обслуживаемые на j-й машине, относятся к разным типам, то j-я машина должен пройти переналадку;

6) Задана матрица производительностей P, элемент P_ij равен времени обслуживания i-й работы на j-й машине;

7) Для каждой машины задана матрица переналадок E, элемент которой E_ir равен времени переналадки машины при переходе с обслуживания работы i-го типа на обслуживание работы r-го типа;

8) Заданы цены единицы времени обслуживания и переналадки каждой машины (соответственно C_j и R_j);

9) Заданы ограничения на сроки выполнения каждой i-й работы: «мягкие» D_i и «жесткие» T_i ограничения, причем T_i>D_i, из-за нарушения сроков налагаются штрафы G₁ и G₂, соответственно, G₂ >>G₁.

Требуется получить расписание, минимизирующее общие затраты, складывающееся из штрафов, затрат на обслуживание всех работ на всех стадиях и затрат на переналадки всех машин.

В экспериментах принято: число работ 94, число машин 15, размер популяции 200. Усредненные по нескольким вариантам расчета зависимости целевой функции F(X) от числа evals обращений к процедуре ее вычисления показаны на рис. 5.

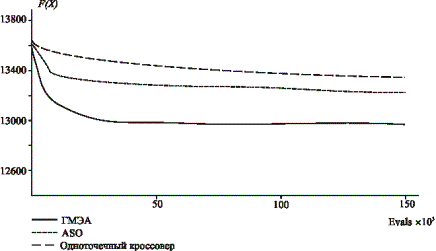
Рис. 5 Сравнительные результаты поиска разными методами

Эксперименты показали, что разработанный ГМЭА обеспечивает результат более точный по сравнению с результатами применения неадаптивных генетических алгоритмов в среднем на 7…10%.

Таким образом, проведенные исследования показали существенное преимущество разработанного алгоритма перед существующими методами, а так же перспективность применения метагенетического подхода, сочетающего ГА и классические методы оптимизации.

Список литературы:

1. Норенков И.П., Арутюнян Н.М. Эволюционные методы в задачах выбора проектных решений // Наука и образование электронное издание №9, 2007

2. Яковлев К.А., Муратов А.В. Разработка модифицированного эволюционного алгоритма решения задач многокритериальной оптимизации на всех этапах жизненного цикла парка транспортно-технологических машин // Вестник Воронежского государственного технического университета − 2010.− Т.6. − №7. − С. 33-38

3. Яковлев К.А. Решение задачи многоцелевой оптимизации подвижности лесотехнических машин // Вестник Воронежского государственного технического университета − 2010.− Т.6. − №7. − С. 64–67

4. Genetic Algorithms (Evolutionary Algorithms): Repository of Test Functions. - http://www.cs.uwyo.edu/~wspears/functs.html.

5. Гладков Л.А. Генетические алгоритмы / Гладков Л.А., Курейчик В.В., Курейчик. – М.: ФИЗМАТЛИТ, 2006. – 243 с.

6. Osyczka A., Kundu S. A new method to solve generalized multicriteria optimization problems using the simple genetic algorithm // Structural Optimization. 1995. Vol. 10. P. 94-99.