Док.техн.наук. Гришин А.П., канд.экон.наук. Гришин А.А.

Применение аппарата нечеткой логики

для автоматизации технических средств сельскохозяйственного назначения

 
 
Нечеткие регуляторы.
Наиболее встречаемым видом неопределенности при решении задач автоматизации технических средств сельскохозяйственного назначения является неопределенность, связанная с невозможностью контроля параметров технологического процесса во всех требуемых точках объекта. И, как следствие, неточность задания переменных в расчетных моделях, начальных и граничных условий.
В начале 1980-х гг. получила развитие теория нечетких множеств и нечеткая логика, позволяющая описывать качественные, неточные понятия и наши знания об окружающем мире, а также оперировать этими знаниями с целью получения новой информации.
Причинами быстрого развития нечеткого моделирования для интеллектуальных систем управления (ИСУ) явились: 
- возможность построения систем управления в условиях, когда имеется информация лишь качественного характера; 
- малая чувствительность систем управления к изменению параметров объекта управления; 
- малая трудоемкость построения систем управления сложными объектами.
Для нечеткого моделирования существуют области, где их применение наиболее предпочтительно: 
- системы регулирования, где модель объекта управления определена лишь качественно; 
- надстройка над традиционными системами регулирования для придания им адаптивных свойств (например, в ПИД-регуляторах); 
- воспроизведение участия человека-оператора в ИСУ. 
Общей предпосылкой для применения нечетких регуляторов существуют два фактора: как уже отмечено выше, наличие неопределенности и наличие информации качественного характера необходимой при построении ИСУ. Последний фактор имеет принципиальное значение, поскольку такой характер информации присущ только интеллекту.
Преимущество ИСУ перед АСУ при управлении сложными технологическими процессами с участием живых организмов обусловлено тем, что они работают не только с количественной информацией, в отличии от традиционных АСУ, но и с качественной информацией, характерной для базы знаний, где заложены причинно-следственные взаимосвязи в каждой конкретной ситуации, информацией о возможном дальнейшем развитии событий в управляющей системе и переходе к другой ситуации в зависимости от предпринятых действий, другой информацией методического характера. 

Например, рассмотрим систему стабилизации давления в сети водоснабжения животноводческого комплекса, оперирующую количественными данными. Сигнал от датчика давления и сигнал, соответствующий желаемому значению давления, поступает к блоку сравнения; блок сравнения вычисляет сигнал рассогласования и выдает его на вход регулятора; регулятор по сигналу рассогласования формирует регулирующее воздействие согласно конкретному фиксированному закону управления (алгоритм работы регулятора будет зависеть от его структуры и метода синтеза); регулирующее воздействие поступает на исполнительный элемент, непосредственно влияющий на давление в сети (частотно-регулируемый насос, электроприводной вентиль); вызванное регулирующим воздействием изменение режима работы исполнительного устройства приводит к изменению давления в сети и его приближению к заданному значению. Работа такой системы будет безупречна, если ее взаимодействие с окружающим миром было формально количественно описано на этапе синтеза регулятора и реально никогда не выходит за рамки этого описания. Но реальный мир одними количественными данными описать нельзя – реальный мир описывается количественными, описываемыми математическими терминами, и качественными, описываемыми средствами естественного языка, знаниями. Поэтому работа такой системы на практике в определенных нештатных ситуациях (т.е. ситуациях, не предусмотренных при синтезе регулятора, а предусмотреть все, как известно, невозможно) будет протекать с точки зрения человека нерационально или даже абсурдно. Представим себе несколько нештатных ситуаций, приводящих к изменению сигнала датчика давления: в сети при максимальном водоразборе произошла авария с разрывом трубопровода; в месте установки датчика происходит утечка воды; датчик вышел из строя и этот список можно продолжить. Во всех случаях автоматика среагирует согласно алгоритму, изменяя давление в сети и его приближая его к заданному значению, что приведет к усугублению нештатной ситуации.

А теперь представим, что стабильное давление в сети пытается поддержать человек, а не вышеописанная АСУ. Сидит человек перед манометром, посматривает на него и, в зависимости от его показаний, поворачивает ручной регулятор преобразователя частоты и меняет производительность насоса. Если манометр выйдет из строя, человек быстро это поймет по своим наблюдениям (допустим, манометр показывает 0,5 атмосферы, а насос работает на полную мощность). Если кто-то ненадолго открыл вентиль, и давление упало по манометру, то человек может ничего и не предпринимать, если уверен, что вентиль вот-вот закроют. Если произошел прорыв трубопровода, и давление резко снизилось, то вместо того, чтобы включать насос на полную мощность, нужно устранить аварию, иначе энергия насоса будет растрачиваться впустую. Такой список нештатных ситуаций для АСУ, в которых человеческое управление предпочтительнее можно продолжить ещё. Почему человек, как «устройство управления», зачастую, оказывается более приемлемым – потому что он обладает не только данными, но и, самое главное, знаниями о данной системе. Знает, что манометр может иногда давать ошибочные показания; знает, что, пока возникшую интенсивную утечку воды перекрыть нельзя, то качать воду в сеть бесполезно; знает ещё много чего, а если чего и не знает, то сможет сделать выводы по наблюдаемым данным, и, таким образом, пополнить свои знания. В отличие от АСУ, человек оперирует не только точной количественной информацией (показаниями манометра), но и качественной информацией: в сети слишком большое давление, а не точной количественной оценкой «давление в сети 10 атмосфер». Имеют место ошибочные показания манометра, а не – «погрешность составляет 25%»; кратковременное незначительное снижение давления, а не – «снижение давления в течение трех секунд на 0,5 атмосферы и т. д. Это объясняется тем, что знания об окружающем нас мире далеко не всегда могут быть четко описаны количественными характеристиками. Поэтому для успешного взаимодействия с реальным миром необходимо оперировать не только количественными, но и качественными знаниями, в том числе неопределенными (нечеткими). Например: давление воды в сети 2 атмосферы (это количественное четкое знание); давление воды в сети значительно выше 0,5 атмосферы (это количественное нечеткое знание).

Математический аппарат.

Математический аппарат нечетких знаний или нечетких множеств, нечеткой логики впервые предложен американским ученым Лотфи Заде (Lotfi Zadeh) в 1965 г. Для описания нечетких множеств вводятся понятия нечеткой и лингвистической переменных.

Характеристикой нечеткого множества выступает функция принадлежности. Обозначим через µf_c(x) – степень принадлежности к нечеткому множеству C. Тогда нечетким множеством С называется множество упорядоченных пар вида C={µf_c(x)/x}, где µf_c(x) [0,1]. Значение µf_c(x)=0 означает отсутствие принадлежности к множеству, 1 – полную принадлежность.

Проиллюстрируем это на простом примере. Формализуем неточное определение «температура почвы». В качестве x (область рассуждений) будет выступать шкала в процентах. Допустим, что она изменяется от 0 до 40⁰С. Нечеткое множество для понятия "оптимальная температура для растения" может выглядеть следующим образом:

C={0/0; 0/5; 0/10; 0,5/15; 0,80/20; 1,0/25; 0,70/30; 0,30/35; 0/40}.

Так, температура почвы 20⁰С принадлежит к множеству "Оптимальная" со степенью принадлежности 0,80. Для определенных растений в определенный этап роста температура почвы 25⁰С будет приближенной к оптимальной, для других растений – слишком высокой. Именно в этом и проявляется нечеткость задания соответствующего множества.

Для нечетких множеств, как и для обычных, определены основные логические операции. Самыми основными, необходимыми для расчетов, являются пересечение и объединение.

Пересечение двух нечетких множеств (нечеткое "И"): A и B: f_AB(x) = min (µf_А(x), µf_В(x)).

Объединение двух нечетких множеств (нечеткое "ИЛИ"): A и B: f_AB(x) = max (µf_А(x), µf_В(x)).

Нечеткая переменная описывается набором (N,X,A), где N – это название переменной, X – универсальное множество (область рассуждений), С – нечеткое множество на X.

Значениями лингвистической переменной могут быть нечеткие переменные, т.е. лингвистическая переменная находится на более высоком уровне, чем нечеткая переменная. Каждая лингвистическая переменная состоит из:

· названия;

· множества своих значений, которое также называется базовым терм-множеством T. Элементы базового терм-множества представляют собой названия нечетких переменных;

· универсального множества X;

· синтаксического правила G, по которому генерируются новые термы с применением слов естественного или формального языка;

· семантического правила P, которое каждому значению лингвистической переменной ставит в соответствие нечеткое подмножество множества X.

Рассмотрим такое нечеткое понятие как Влажность зерна. Это и есть название лингвистической переменной. Сформируем для нее базовое терм-множество, которое будет состоять из трех нечетких переменных: "Низкая", "Умеренная", "Высокая" и зададим область рассуждений в виде X=[0;100] (%). Последнее, что осталось сделать – построить функции принадлежности для каждого лингвистического терма из базового терм-множества T.

Существует свыше десятка типовых форм кривых для задания функций принадлежности. Наибольшее распространение получили: треугольная, трапецеидальная и гауссова функции принадлежности.

Треугольная функция принадлежности определяется тройкой чисел (a,b,c), и ее значение в точке x вычисляется согласно выражению:

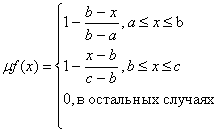
При (b-a)=(c-b) имеем случай симметричной треугольной функции принадлежности, которая может быть однозначно задана двумя параметрами из тройки (a,b,c).

Аналогично для задания трапецеидальной функции принадлежности необходима четверка чисел (a,b,c,d):

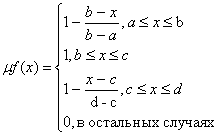
При (b-a)=(d-c) трапецеидальная функция принадлежности принимает симметричный вид.

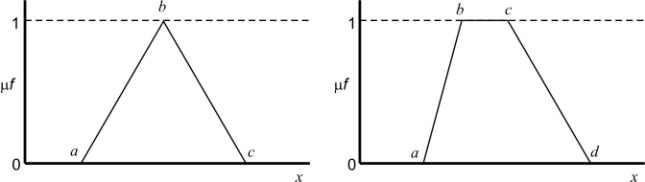
Рис. 1. Типовые кусочно-линейные функции принадлежности.

Функция принадлежности гауссова типа описывается формулой

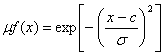
и оперирует двумя параметрами. Параметр c обозначает центр нечеткого множества, а параметр σ отвечает за крутизну функции.

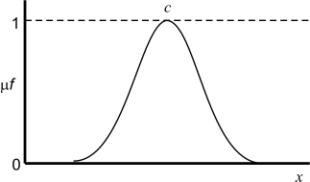
Рис. 2. Гауссова функция принадлежности.

Совокупность функций принадлежности для каждого терма из базового терм-множества T обычно изображаются вместе на одном графике. На рис. 3 приведен пример описанной выше лингвистической переменной "Влажность зерна" для значения X=62,0%, на рис. 4 – формализация неточного понятия «загрязнение зерна примесями". Так, для зерна с 15% примесей степень принадлежности к множеству "Низкое" равна 0,20, "Среднее" – 0,47, "Высокое" – 0,0.

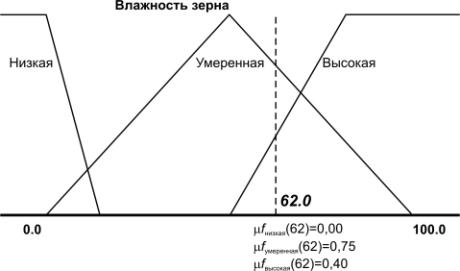
Рис. 3. Описание лингвистической переменной "Влажность зерна".

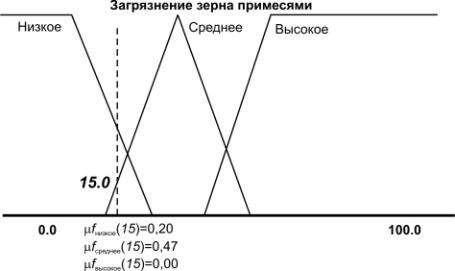
Рис. 4. Описание лингвистической переменной "Загрязнение зерна примесями".

Количество термов в лингвистической переменной редко превышает 7.

Практика применения.

Основой для проведения операций нечеткой логики является база правил, содержащая нечеткие высказывания в форме "Если-то" и функции принадлежности для соответствующих лингвистических термов. Они позволяют при построении нечетких регуляторов осуществлять нечеткие выводы. При этом должны соблюдаться следующие условия:

1. Существует хотя бы одно правило для каждого лингвистического терма выходной переменной.

2. Для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки (левая часть правила).

В противном случае имеет место неполная база нечетких правил.

Пусть в базе правил имеется m правил вида:

R₁: ЕСЛИ x₁ это A₁₁ … И … x_n это A_1n, ТО y это B₁ …

R_i: ЕСЛИ x₁ это A_i1 … И … x_n это A_in, ТО y это B_i…

R_m: ЕСЛИ x₁ это A_i1 … И … x_n это A_mn, ТО y это B_m,

где x_k , k=1..n – входные переменные; y – выходная переменная; A_ik – заданные нечеткие множества с функциями принадлежности.

Результатом нечеткого вывода является четкое значение переменной y^* на основе заданных четких значений x_k , k=1..n.

В общем случае механизм логического вывода включает четыре этапа: введение нечеткости (фазификация), нечеткий вывод, композиция и приведение к четкости, или дефазификация (см. рис. 5).

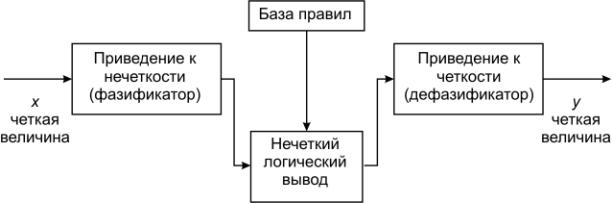
Рис. 5. Система нечеткого логического вывода.

Алгоритмы нечеткого вывода различаются главным образом видом используемых правил, логических операций и разновидностью метода дефазификации. Разработаны модели нечеткого вывода Мамдани, Сугено, Ларсена, Цукамото.

Наиболее распространенный способ логического вывода в нечетких регуляторах – вывод Мамдани. В нем используется минимаксная композиция нечетких множеств. Данный механизм включает в себя следующую последовательность действий.

1. Процедура фазификации: определяются степени истинности, т.е. значения функций принадлежности для левых частей каждого правила (предпосылок).

2. Нечеткий вывод. Сначала определяются уровни "отсечения" для левой части каждого из правил. Далее находятся "усеченные" функции принадлежности.

3. Композиция, или объединение полученных усеченных функций, для чего используется максимальная композиция нечетких множеств.

4. Дефазификация, или приведение к четкости. Существует несколько методов дефазификации. Например, метод среднего центра, или центроидный метод.

Геометрический смысл такого значения – центр тяжести для кривой µf_c(y). Рис. 6 графически показан процесс нечеткого вывода по Мамдани для двух входных переменных и двух нечетких правил R1 и R2.

Таким образом, для того чтобы интеллектуальная САУ обладала близкой к человеческой возможностью работы со знаниями, необходима их формализация и представление в технической системе посредством некоего языка описания знаний, категориями которого система могла бы оперировать так же, как человек словами. Также очевидно, что для достижения большего эффекта интеллектуализации технической системы этот язык должен описывать все возможные виды знаний: количественные и качественные, четкие и нечеткие.

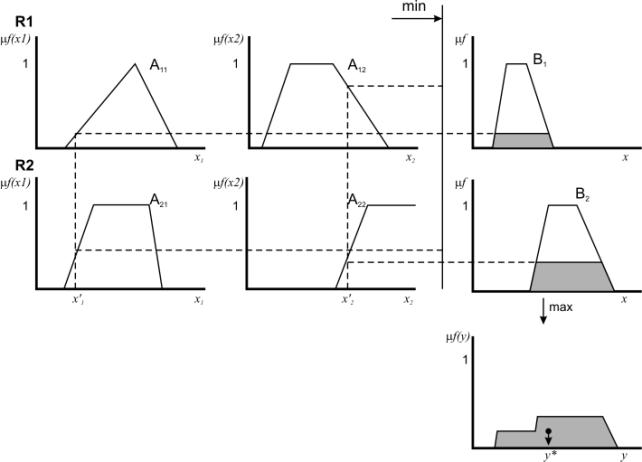
Рис. 6. Схема нечеткого вывода по Мамдани.

Проиллюстрируем этот подход на простом примере управления глубиной погружения в почву рабочего органа почвообрабатывающей машины при вспашке. Входным точным значением здесь является плотность почвы ρ, а выходным - длительность действия актуатора t – приводного механизма поступательного движения рабочего органа, определяющего глубину его погружения в почву.

Введем две лингвистические переменные: "плотность почвы" с термами "малая", "средняя", "большая". И "длительность поступательного движения актуатора" с термами "короткая", "средняя", "большая". Соответствующие входные и выходные функции принадлежности приведены на рисунке 7а и 7б. Нечеткая инструкция управлением этой системой может сводиться к трем простым правилам: 1) при малой плотности длительность поступательного движения актуатора должна быть короткой, 2) средней плотности должна соответствовать средняя длительность поступательного движения актуатора, 3) в случае большой плотности требуется большая длительность поступательного движения актуатора.

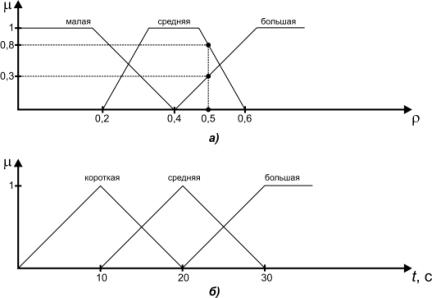
Рис. 7. Входные и выходные функции принадлежностей лингвистических переменных "плотность почвы" а) и "длительность поступательного движения актуатора" б).

Как следует из рисунка 7а, области определения входных функций принадлежности различных термов пересекаются, поэтому выходная нечеткая инструкция будет представляться некоторой комбинацией приведенных правил. При этом естественно предположить, что в эту комбинацию отдельные правила будут входить с коэффициентами, определяемыми степенями принадлежности точных исходных данных соответствующим термам.

Пусть зафиксированное в некоторый момент значение плотности ρ равно 0,5. Процедура фаззификации показывает, что эта плотность со степенью 0,3 принадлежит терму "большая плотность" и со степенью 0,8 - терму "средняя плотность", а к терму «низкая плотность» не принадлежит. Согласно принятому правилу комбинирования нечетких выходных инструкций, длительность поступательного движения актуатора должна быть на 0,3 большой и на 0,8 средней. Конкретные правила дефаззификации могут быть различными. Мы применим центроидный:

Где t_б и t_с – длительности поступательного движения актуатора, при которых выходные функции принадлежности соответствующих термов ("большая" и "средняя") принимают максимальные значения. В нашем случае t = 24,2 с.

Рамки доклада, к сожалению, не позволяют нам сейчас провести дальнейший очерк классов ИСУ для автоматизации сельхозпроизводства, основанных на нейронных сетях и генетических алгоритмах.

Сейчас ясно одно: затронутая проблема весьма актуальна на сегодняшний день потому, что ни один из упомянутых классов, как впрочем и сами ИСУ пока не получили широкого распространения при создании устройств автоматизации сложных динамических систем в машинах и машинных технологиях сельскохозяйственного производства. Еще требуется проведение НИР с целью научного обоснования применения ИСУ в сельском хозяйстве, создания теоретической основы их разработок для решения таких конкретных задач, как, например в растениеводстве:

- создание первичных преобразователей физиологических параметров и характеристик различных культур в электрические сигналы для мониторинга состояния растений в интенсивных технологиях.

- создание интенсивных интеллектуальных технологий возделывания культур и получения семенного материала на основе принципов слежения за отдельными физиологическими процессами в растениях, регистрации их и согласования воздействия внешних условий (светового, температурного и питательного режима, влажности и содержания СО₂) с физиологическим состоянием растения по программе, задаваемой самим растением;

- создание первичных преобразователей агротехнических параметров и характеристик сельскохозяйственных объектов и организмов, участвующих в интеллектуальных, роботизированных агротехнологиях для мониторинга этих параметров и характеристик;

- создание интеллектуальных машин и машинных технологий для растениеводства на основе динамичного перехода от интеллектуализации отдельных операционных узлов и рабочих органов машин в сфере почвообработки, посева, ухода за насаждениями, уборки урожая и послеуборочной обработки урожая до создания интеллектуальных роботизированных комбайнов и агротехнологий;

- разработка теоретических основ, методик, рекомендаций, базы знаний и базы данных для специалистов профильных лабораторий и отделов механизации растениеводства в области создания интеллектуальных систем управления.

Гибридизация методов интеллектуальной обработки информации – девиз, под которым прошли 90-е годы у исследователей ИСУ. В результате объединения нескольких технологий искусственного интеллекта появился специальный термин – "мягкие вычисления" (soft computing), который ввел Л. Заде в 1994 году. В настоящее время мягкие вычисления объединяют такие области как: нечеткая логика, искусственные нейронные сети, вероятностные рассуждения и эволюционные алгоритмы. Они дополняют друг друга и используются в различных комбинациях для создания гибридных интеллектуальных систем.

Влияние нечеткой логики оказалось, пожалуй, самым обширным. В условиях реального мира знания качественного характера обладают не меньшей, а, зачастую, гораздо большей полезностью, чем знания количественные. Более того, большинство проблем человеку приходится решать изначально опираясь только на нечеткие знания.