Technical science

Zhussupova B.T., Chromushina М.Е.

A.Baitursynov Kostanay State University

POSSIBILITY TO REALIZE THE MODULE OF FUZZY-NEURAL CONTROL USING FUZZY LOGIC TOOLBOX

Abstract

In our days there is a need for systems that can not only be performed once programmed sequence of actions with pre-defined data but also able to analyze incoming information, search and find patterns to make predictions, etc. In this area of application in the best way proved neural network. This area explores the intelligent methods to solve various tasks used in various areas, including in industry, economy, medicine, and other. The intelligent computing systems (ICS), representing an association of neural networks, genetic algorithms and fuzzy systems, allow to solve various tasks, but the most important thing - they become a universal tool for information processing.

Key words: neural networks, fuzzy system, membership function, forecasting.

I. Introduction

Thanks to the development and publications of L. Zadeh, E. Mamdani, M, Sugeno has identified a range of possible applications of fuzzy set theory ( FST) for practical tasks, in which the object and terms of its functioning poorly understood, the model of the object and purpose of management of poorly formalized. Using traditional approaches, it is difficult to get adequate model of the processes, taking into account the available expert knowledge [1]. Note that often we come to the conclusion, acting on the basis of linguistic rules, in which is concentrated theoretical knowledge and personal experience of management. To turn such expert rules in the mathematical model is conveniently using FST. It is possible to implement such model with the help of means of “Fuzzy Logic Toolbox” of “Matlab” package.

II. Task Statement

Let's say, we will call predicted criterion number . Many different factors influence this criterion. Designate them through , then the model of this criterion will represent functional display of a look: , where - vector of influencing factors. At a large number of factors it is convenient to classify their influence in the form of a hierarchical tree of a logical conclusion. Elements of a tree it is interpreted so: tree root – criterion ; terminal tops – private influencing factors of influence (); non-terminal tops – parcels of influencing factors; arcs of the graph out of non-terminal tops – enlarged influencing factors ().

Rollups and are implemented through the logical conclusion of the fuzzy knowledge bases. Values of factors are expressed as a deviation (in percent) from average indicators. For modeling of the integrated influencing factors expert fuzzy knowledge bases type Mamdani are used. Elements of antecedents of indistinct rules communicate logical operation And. For modeling of considered criterion the fuzzy knowledge base type Sugeno is offered. Each rule of this knowledge base models one type of marketing. The coefficients in the conclusions of the rules define the sensitivity criterion for the relevant factors. The coefficients are selected expertly by the method of paired comparisons Saati.

For getting the graphs of the membership functions of fuzzy therms "Low" (L), Medium (M) and High (H) is used membership function of Gauss. , where – the membership function of the factor to the fuzzy number ; and  – the parameters of the membership function: the coordinate of the maximum and the coefficient of concentration.

In a clear case the extent of membership is calculated by substituting the current value of the variable in the formula for calculating . When we have fuzzy source data it is necessary to determine the extent of membership of one of fuzzy set  – the values of the input variable, to another fuzzy set – to the therm from the knowledge base, which is equal to the height of the intersection of these fuzzy sets. When creating a fuzzy model of the considered criteria systems of fuzzy output for each factor are implemented in the Fuzzy Logic Toolbox of Matlab package.

III. Results

For the implementation of the fuzzy model of competitiveness of the University are use four systems of fuzzy conclusion [3, c.255-276]:

y1_Quality.fis – fuzzy modeling system of quality of the University (y₁).

y2_Image.fis - fuzzy modeling system of the image of the University (y₂).

y3_Service.fis - modeling system of the Service (y₃).

Q_Competitive Strength Index.fis - fuzzy system of forecasting of competitiveness of the University (Q).

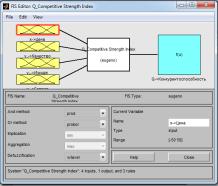
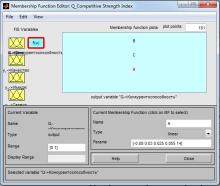
Picture 1 – Membership functions of competitiveness

The interface of model is realize using a system GUI. When you click to “Rate competitiveness” is a function conc.m. call.

IV. Conclusions

This interface is simple, intuitive and does not require much explanation: the source data are entered in the text boxes according to the legend (L - low, BA - below average, A - average, UM - upper-middle, UI - upper intermediate)

Literature:

1. Лукас В.А. Введение в Fuzzy-регулирование. – Екатеринбург: Изд-во УТГГА, 1997. – 36 с.

2. http://matlab.exponenta.ru.

3. Горбань А.Н. Нейронные сети на персональном компьютере. / А. Горбань, Д. Россиев. – Новосибирск.: Наука, 1996. – C. 255-276.