Engineering sciences. Effective tools of modern science – 2014

Graduate student V. A. Ruk, Doctor of Engineering Sciences, professor A. Nurzhauov

Pavlodar State University named after S. Torayghyrov, Kazakhstan

The definition of the moments of inertia in the pinion of transport vehicle’s transmission

While doing the theoretical study of movement of transport vehicles arises necessity in their dynamic modeling. Dynamic model of transport vehicle is represented as rotationally or translationally moving masses, applied to the shaft and connected between each other by elastic connections. The quantity of masses and the degree of freedom in the system depend on the specific approach to the solution of the problem. The measure of inertia in the applied rotational mass determines by the applied moment of inertia relative to the axis of rotation. For the definition of the value of applied moment of inertia it is necessary to know moments of inertia of every mass relative to its own axis of rotation, which will be led to the axis of adduction then. The construction of transport vehicle consists of big quantity of joints and aggregates, which have very different configurations. The definition of the moments of inertia in all details is not possible. At the same time, it’s possible to determine theoretically in the first approximation moments of inertia of details by the analyzing of their construction and by the defining of their locations and kinds of moving. In the transmission of transport vehicle the most common details are cylindrical pinions. For the definition of the moment of inertia relative to the axis of rotation let’s take like an example the pinion of seventh gear, located on the secondary shaft in gearbox of crawler tractor DT-75M ‘Kazakhstan’. 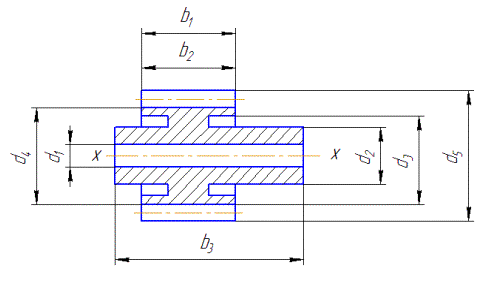The sketch of this pinion is shown at the figure 1.

Axial moment of inertia is the sum of multiplication of points’ masses in this system and of squaring of distances from the axis [1]:

where – moment of inertia of system relative to the axis Ox;

m_i – mass of point i in the system;

r_i – distance of this point from the axis.

Figure 1 – The sketch of pinion

For the definition of moment of inertia of pinion let’s divide it to the simple geometrical parts.

At the picture pinion is shown like a detail, consisted of cylindrical parts with the diameter d_i and the length b_i (i = 1, 2, … - numbers of parts). By looking at the sizes of parts and by the using of known formulas it’s possible to determine the values of volumes V_i. Also by the using of drawings or parts’ catalog we can find the weight of detail and its mass.

While determining of axial moment of inertia we can divide the pinion to four parts. Three parts are thick-walled hollow cylinders. The fourth part consists of teeth and empty spaces between neighboring teeth, surrounded mentally by cylindrical surfaces in the foot and top of teeth.

The moment of inertia of hollow cylinder with mass m, outer radius R₁ and inner radius R₂ is determined by the formula [2, 3]:

According to this formula the moment of inertia of thick-walled hollow cylinder with inner diameter d₁, outer diameter d₂ and height b₃ is determined by the formula:

The mass of thick-walled cylinder m₁ is determined from the formula:

where ρ – density of the pinion.

By analogy let’s make the formulas of two next thick-walled hollow cylinders with inner diameters d₂ and d₃, outer diameters d₃ and d₄ and heights b₂ и b₁:

Then we will accept that moment of inertia of teeth in the pinion is equal to the half of moment of inertia of hollow cylindrical body relative to its axis, coincident to the axis of pinion. Now we can determine the moment of inertia of fourth part in our pinion [4]:

where m_ц – mass of hollow cylindrical body with the length b₁, inner diameter d₄ and outer diameter d₅.

Moment of inertia of examined pinion relative to the axis x, passing the centre of masses, is equal to the sum of moments of inertia of its parts, determined relative to this axis:

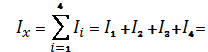
Axial moments of inertia in similar from the view of geometry pinions of other mechanisms in transport vehicles are determined by this formula. For details with other construction formulas must be created with the sequence, described above.

Literature:

1 Савин Г. Н., Путята Т. В., Фрадлин Б. Н. Курс теоретической механики. Издательское объединение «Вища школа», 1973, 360 с.

2 Дерюгин Е. Е. Динамика вращательного движения абсолютно твердого тела [Текст]: учебное пособие / Е. Е. Дерюгин, Л. А. Теплякова. – Томск: Изд-во Том. гос. архит.-строит. ун-та, 2010. 65 с.

3 Whittaker E. T. A Treatise on the Analitical Dynamics of Particles and Rigid Bodies. Библиотека “R&C Dynamics”, 1999, 587 с.

4 Нуржауов А. Н. Исследование динамики гусеничного трактора класса 30 – 40 кН тяги и ресурса его планетарного механизма поворота : монография. – Павлодар: Кереку, 2009. – 329 с.