УДК 519. 624
Жүктелген дифференциалдық
теңдеулер үшін шеттік
есепті шешудің бір сандық әдісі
ф.-м.ғ.к.
К.Ж.Назарова , оқытушы Б.Ж.Алиханова А
Ясауи атындағы ХҚТУ
Әртүрлі
физикалық құбылыстарды зерттеуде дифференциалдық теңдеулермен қатар
интегро-дифференциалдық теңдеулер қажеттігі туындайды.
Интегро-дифференциалдық теңдеулердің жуықтау шешімін
іздестіру барысындағы интегро-дифференциалдық мүшені
квадратуралық формуламен
алмастыруда жүктелген
дифференциалдық теңдеулер алынады. Қолданбалы математиканың көптеген есептері жәй
дифференциалдық теңдеулер үшін екі нүктелі шеттік есептерге келтіріледі. Сондықтан,
жүктелген жәй
дифференциалдық теңдеулер үшін шеттік есептердің
зерттелуінің ғылымдағы
орны ерекше. Жүктелген дифференциалдық теңдеулерді шешуде
жәй дифференциалдық теңдеулер үшін шеттік есептер теориясының әдістері
қолданылады.
![]() кесіндісінде екінші ретті жүктелген дифференциалдық теңдеу үшін екі нүктелі шеттік есепті қарастырайық
кесіндісінде екінші ретті жүктелген дифференциалдық теңдеу үшін екі нүктелі шеттік есепті қарастырайық
![]() (1)
(1)
![]() (2)
(2)
Мұндағы
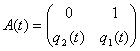 ,
, 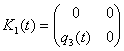 ,
, 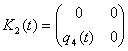 ,
, ![]() -
- ![]() -да үзіліссіз.
-да үзіліссіз.
![]() ,
, ![]() .
.
(1), (2) есебінің шешімі деп (1) дифференциалдық
теңдеуін, (2) шеттік шартын қанағаттандыратын, ![]() -да үзіліссіз дифференциалданатын
-да үзіліссіз дифференциалданатын ![]() вектор-функцияны
айтады.
вектор-функцияны
айтады.
Анықтама. Егер кез-келген ![]() үшін (1), (2)
есебінің жалғыз шешімі болса, онда ол бірмәнді
шешілімді.
үшін (1), (2)
есебінің жалғыз шешімі болса, онда ол бірмәнді
шешілімді.
(1) теңдеуінде
![]()
белгілеуін енгізсек, онда мынадай теңдеулер жүйесін
аламыз:
![]()
![]() біртекті теңдеудің
фундаменталды шешімі болсын.
біртекті теңдеудің
фундаменталды шешімі болсын.
Берілген ![]() аралық 3 бөлікке бөлінеді:
аралық 3 бөлікке бөлінеді:
![]() әрбір
интервалдағы
әрбір
интервалдағы ![]() функциясының
сығылуын
функциясының
сығылуын ![]() деп
белгілейік.
деп
белгілейік.
![]() белгілеулер енгізіп
белгілеулер енгізіп
![]()
интервалдарында ![]()
алмастыруларын енгіземіз. Сонда (1) – (2) есебі
эквивалентті, көпнүктелі параметрлі шеттік есепке келтіріледі.
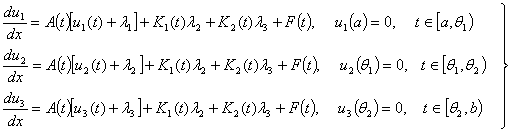 (3)
(3)
![]() , (4)
, (4)
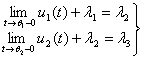 (5)
(5)
Біртекті дифференциалдық теңдеуінің
![]() - фундаменталды
матрицасын пайдаланып (3) есебінен эквивалентті интегралдық теңдеулер
жүйесіне көшеміз:
- фундаменталды
матрицасын пайдаланып (3) есебінен эквивалентті интегралдық теңдеулер
жүйесіне көшеміз:
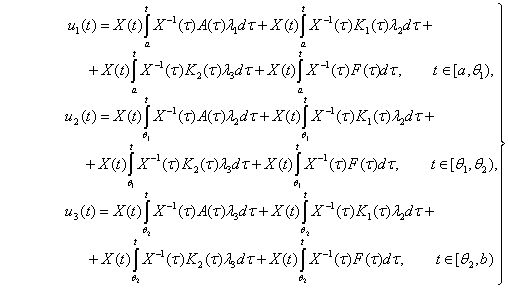 (6)
(6)
Осы теңдіктер арқылы ![]() шектерін анықтап
(4), (5) шеттік шарттарына қоямыз. Сонда белгісіз параметрлерді анықтайтын
келесі теңдеулер жүйесін аламыз:
шектерін анықтап
(4), (5) шеттік шарттарына қоямыз. Сонда белгісіз параметрлерді анықтайтын
келесі теңдеулер жүйесін аламыз:
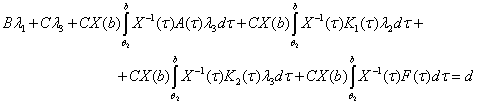 (7)
(7)
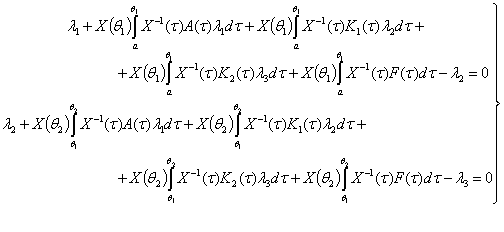 (8)
(8)
Бұл теңдеулер жүйесін
векторлық түрде былай жазуға болады:
![]() , (9)
, (9)
мұндағы
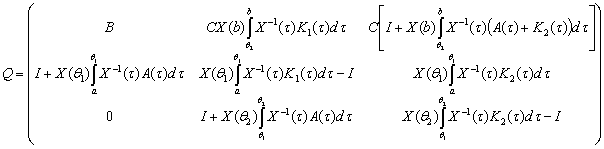 ,
,
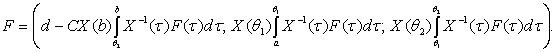
Сонымен ![]() жұбы, (3) – (5)
есебінің шешімін табу үшін (6) интегро-дифференциалдық теңдеуі үшін Коши есебі мен (9) сызықты теңдеулер жүйесін
бірге шығарамыз.
жұбы, (3) – (5)
есебінің шешімін табу үшін (6) интегро-дифференциалдық теңдеуі үшін Коши есебі мен (9) сызықты теңдеулер жүйесін
бірге шығарамыз.
Ол үшін
мынадай алгоритм ұсынамыз:
а) Таңдап
алынған ![]() үшін
үшін ![]() матрицасына кері
матрица бар деп жорамалдап
матрицасына кері
матрица бар деп жорамалдап ![]()
сызықты теңдеулер жүйесінен ![]() параметрін табамыз, яғни:
параметрін табамыз, яғни:
![]() .
.
б) Әрбір интервалда ![]() ,
,![]() табылған
параметрдің
табылған
параметрдің ![]() сәйкес мәнінде (9)
Коши есебін шығарып
сәйкес мәнінде (9)
Коши есебін шығарып ![]()
шешімін аламыз. Бастапқы
берілген теңдеудің шешімі
![]()
функциялар жүйесі болады.
Теорема 6. (1), (2) есебі бірмәнді
шешілімді болу үшін ![]() матрицасының
кері матрицасы бар болуы қажетті және жеткілікті.
матрицасының
кері матрицасы бар болуы қажетті және жеткілікті.
![]() кесіндісінде екінші ретті жүктелген дифференциалдық теңдеу үшін екі нүктелі шеттік есепті қарастырайық
кесіндісінде екінші ретті жүктелген дифференциалдық теңдеу үшін екі нүктелі шеттік есепті қарастырайық
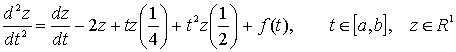 (10)
(10)
![]() (11)
(11)
![]() функцциясы
функцциясы ![]() де үзіліссіз.
де үзіліссіз.
(10), (11) есебін матрицалық түрде жазамыз:
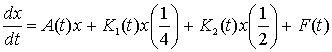 (12)
(12)
![]() (13)
(13)
Мұндағы
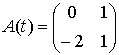 ,
, 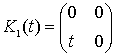 ,
, 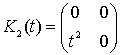 ,
, ![]() -
- ![]() -да
-да
үзіліссіз
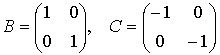 ,
, ![]() .
.
(12) теңдеуінде 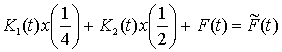
белгілеуін енгіземіз. ![]()
![]()
(12) ![]() біртекті теңдеудің фундаменталды
шешімі, өйткені
біртекті теңдеудің фундаменталды
шешімі, өйткені
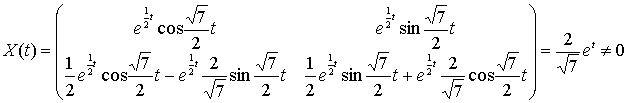
(12),(13) есебіне параметрлеу әдісін қолданамыз.
Берілген ![]() аралық 3 бөлікке бөлінеді:
аралық 3 бөлікке бөлінеді: 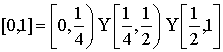 . Әрбір интервалдағы
. Әрбір интервалдағы ![]() функциясының
сығылуын
функциясының
сығылуын ![]() деп
белгілейміз.
деп
белгілейміз.
![]() белгілеулер енгізіп
әрбір интервалда
белгілеулер енгізіп
әрбір интервалда ![]() алмастыру-ларын жасаймыз. Сонда (12) , (13) есебі
эквивалентті, көпнүктелі параметрлі шеттік есепке келтіріледі.
алмастыру-ларын жасаймыз. Сонда (12) , (13) есебі
эквивалентті, көпнүктелі параметрлі шеттік есепке келтіріледі.
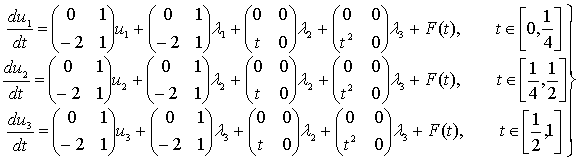 (14)
(14)
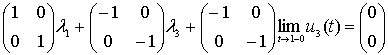 , (15)
, (15)
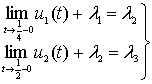 (16)
(16)
Біртекті дифференциалдық теңдеудің ![]()
![]() - фундаменталды шешімдерін пайдаланып
(14) есебінен эквивалентті
интегралдық теңдеулер жүйесін аламыз. Интегралдық теңдеудің
оң жағын шеттік және үзіліссіздік
шартына қоямыз, сонда
- фундаменталды шешімдерін пайдаланып
(14) есебінен эквивалентті
интегралдық теңдеулер жүйесін аламыз. Интегралдық теңдеудің
оң жағын шеттік және үзіліссіздік
шартына қоямыз, сонда ![]() параметріне байланысты сызықты теңдеулер жүйесін
аламыз:
параметріне байланысты сызықты теңдеулер жүйесін
аламыз:
![]()
мұндағы
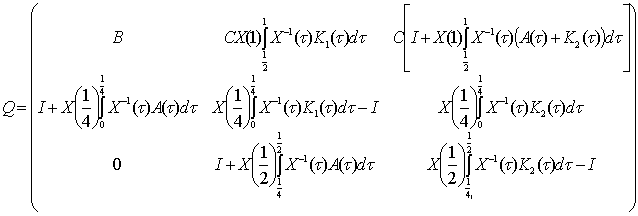
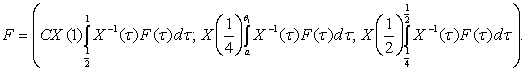
Сонымен ![]() -жұбы көпнүктелі
параметрлі шеттік есеп шешімін табу үшін
мынадай алгоритм ұсынылады:
-жұбы көпнүктелі
параметрлі шеттік есеп шешімін табу үшін
мынадай алгоритм ұсынылады:
а) Таңдап
алынған ![]() үшін
үшін ![]() матрицасына кері
матрица бар деп жорамалдап
матрицасына кері
матрица бар деп жорамалдап
![]()
сызықты теңдеулер жүйесінен ![]() параметрін табамыз, яғни:
параметрін табамыз, яғни:
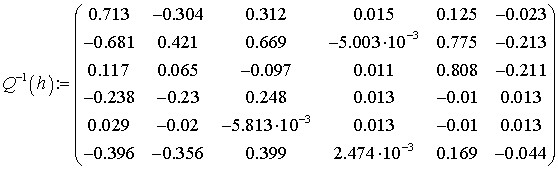
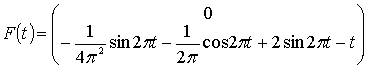
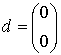
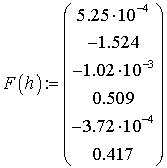
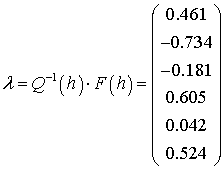
б) Әрбір интервалда ![]() ,
,![]() табылған
параметрдің
табылған
параметрдің ![]() сәйкес мәнінде Коши есебін шығарып
сәйкес мәнінде Коши есебін шығарып ![]() шешімін аламыз.
Сол әдістердің арасындағы көп қолданылатыны ол Рунге – Кутта әдісі. Коши есебін шығару үшін осы әдіске
бағдарлама құрылды.
шешімін аламыз.
Сол әдістердің арасындағы көп қолданылатыны ол Рунге – Кутта әдісі. Коши есебін шығару үшін осы әдіске
бағдарлама құрылды.
Бастапқы
берілген теңдеудің шешімі
![]()
функциялар жүйесі болады. Егер
![]() жұбы
параметрлі көпнүктелі шеттік есеп
шешімі болса, онда функциялар жүйесі
жұбы
параметрлі көпнүктелі шеттік есеп
шешімі болса, онда функциялар жүйесі
![]() (10) – (11) есебінің шешімі болады.
(10) – (11) есебінің шешімі болады.
Пайдаланылған әдебиеттер
тізімі:
12. Джумабаев Д.С. Признаки
однозначной разрешимости линейной краевой задачи для обыкновенного
дифференциального уравнения// Ж. Вычисл. матем. и матем.физ. -1989.-Т.29, №1,
-С.50-66.