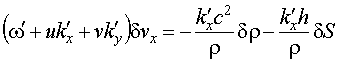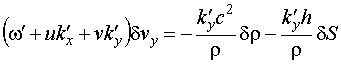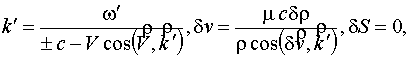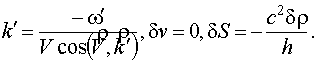Математика/5. Математическое моделирование

К.т.н. Бойчук И.П., к.т.н. Карташев А.С.

Белгородский государственный технологический университет
им. В.Г. Шухова, Россия,
Национальный аэрокосмический университет им. Н.Е. Жуковского «ХАИ», Харьков, Украина

Взаимодействие звуковой волны с головной ударной волной

При движении тел со сверхзвуковой скоростью в среде возникают так называемые скачки уплотнения, или ударные волны. Эти скачки распространяются на большое расстояние от движущегося тела, взаимодействуя со звуковыми волнами. В результате взаимодействия меняются характеристики всех величин среды, что приводит к изменению и звуковых волн. Взаимодействие звуковой волны со скачком уплотнения в одномерном случае было рассмотрено в [1].

Пусть ударная волна (прямой скачек уплотнения), лежащий в плоскости

, движется в положительном направлении оси со скоростью . Навстречу ему распространяется звуковая волна (рис.1).

Для рассмотрения распространения звука воспользуемся уравнениями акустики неоднородной и движущейся среды, полученными Блохинцевым [1]:

,	(1)
,	(2)
,	(3)
, , .	(4)

В этих уравнениях исходное (невозмущенное) состояние среды описывается величинами – скорость, давление, плотность и энтропия. Звук, как малые колебания, описывается величинами: – скорость звуковых колебаний, – давление звука, – изменение плотности среды, – изменение ее энтропии, происходящее при прохождении звуковой волны.

Рис. 1 Схема взаимодействия ударной волны со звуковой волной

В двумерном случае уравнения (1) – (4) есть:

,	(5)
,	(6)
,	(7)
,	(8)
, .	(9)

Поскольку предполагается, что постоянны по обе стороны от скачка, то величинами пренебрегаем.

Перейдем в систему координат, в которой скачек покоится –,. В этой системе скорость среды равна . Тогда уравнения (5) – (9) примут вид:

,	(10)
,	(11)
,	(12)
.	(13)

Предположим, что падающая волна есть гармоническая. Тогда положим, что пропорциональны , где – частота в системе , – компоненты волнового вектора . Подставляя в уравнения (10) – (13), получим:

,	(14)
,	(15)
,	(16)
.	(17)

Система (14) – (17) позволяет получить два решения: либо , либо . Рассмотрим эти случаи. В первом случае из уравнений (14) – (16) получаем:

(18)

где . Это решение представляет адиабатическую волну с фазовой скоростью .

Во втором случае решение суть:

(19)

В этой волне имеют место изменения плотности среды и изменение энтропии . Скорость звуковых колебаний равна нулю. Поскольку , то из последнего уравнения (19) получаем , т.е. волна не вызывает изменения давления в среде. Эта волна движется со скоростью, равной скорости движения среды, т.е. переносится средой. Такие волны называются энтропийными [2].

Таким образом, имеем два рода проходящих волн. Первый – изоэнтропичные волны (18). Второй – это колебания энтропии, распространяющиеся в виде волн (19), которые порождены необратимыми процессами в скачке уплотнения.

Литература:

1. Блохинцев Д.И. Акустика неоднородной движущейся среды: – М: Наука, 1981. – 208 с.

2. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. Теоретическая физика: т.VI. – М.: Наука. Гл. ред. физ–мат. лит., 1986. –736 с.
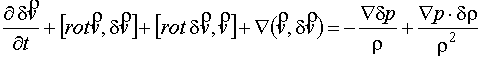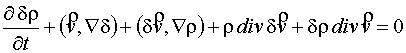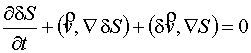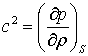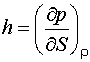
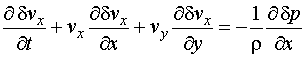
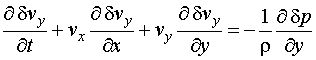
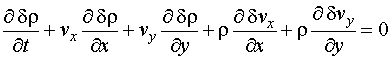
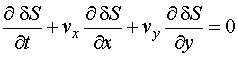
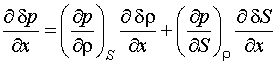
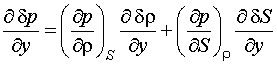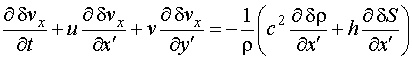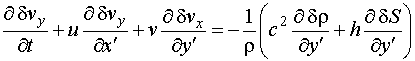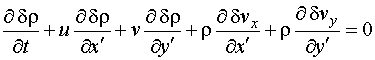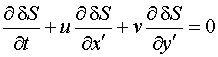