К расчету подкрепленных пологих оболочек

Трубачев С.И., к.т.н., доцент НТУУ «КПИ», Яхно Б.О., к.т.н., доцент НТУУ «КПИ»

В литературе, посвященной теории оболочек, известен целый ряд вариантов уравнений статики и динамики ребристых оболочек. Классификацию большинства из этих вариантов производят по способам А.И.Лурье и В.Э.Власова [ 1 ].

Метод А.И.Лурье

1. Формулируют геометрические условия сопряжения стержней и оболочки.

2. Записывают выражение для полной потенциальной энергии ребристой оболочки в виде суммы потенциальных энергий оболочки и стержней.

3. Обобщенные силы в выражении для потенциальной энергии стержней выражают через обобщенные смещения с помощью одномерного закона Гука.

4. Обобщенные смещения стержней выражают через соответствующие смещения оболочки с помощью геометрических уравнений сопряжения.

5. Из выражения для полной потенциальной энергии на основе принципа возможных перемещений получают уравнения равновесия ребристой оболочки в смещениях.

Метод В.З. Власова

1. Формулируют геометрические условия сопряжения стержней и оболочки

2. Стержни мысленно отделяют от оболочки, относя их реакции к внешним поверхностным силам.

3. Соответствующие названным реакциям силы, действующие на стержень, выражают с помощью уравнения Кирхгофа через усилия и моменты в стержнях

4. Усилия и моменты в стержнях выражают через параметры деформации с помощью одномерного закона Гука для стержней.

5. Параметры деформации стержня выражают через смещения точек его оси с помощью уравнения Клебша и далее с использованием условия сопряжения – через смещения оболочки.

Таким образом, реакции стержней в обоих методах, а вернее путях вывода уравнений статики ребристых оболочек, является лишь выбор соотношений, связывающих усилия и моменты в стержне с деформациями его оси (закон Гука). При одном и том же законе Гука оба пути приводят к одинаковым уравнениям ребристых оболочек.

Подход А.И.Лурье и В.З.Власова основываются на объединении уравнений, описывающих деформацию оболочки (в соответствии с гипотезой Кирхгофа) и деформацию стержней (в соответствии с гипотезой жестких сечений). Построенная таким образом теория ребристых оболочек, как конгломерат теории оболочек и теории стержней, имеет ряд противоречий, заключающихся в том, что:деформация ребристых оболочек описывается системой уравнений двенадцатого порядка, содержащей ряд слагаемых, не имеющих механического смысла в теории оболочек, например, четвертые производные от тангенциальных смещений; уравнения теории ребристых оболочек являются несопряженными и имеют неэллиптический тип. Тем не менее все эффективно используемые уравнения ребристых оболочек построены именно на объединении уравнений теории оболочек и теории стержней.

При большом числе часто расставленных ребер применяется метод приведения ребристой оболочки. Понятно, что при этом напряженно-деформированное состояние вблизи ребер искажается. Имеется ряд нерешенных вопросов: нет четко установленных критериев применимости, т.е. при каком числе и расстоянии между ребрами допустимо их «размазывание»; в ряде случаев формулы определения приведенной жесткости либо отсутствуют, либо не имеют достаточных обоснований (например, при косоугольной сетке ребер); отсутствуют рекомендации для нерегулярной расстановки ребер. В связи с этим ниже рассматриваются лишь методы, учитывающие дискретную постановку.

Трудности аналитических решений обуславливаются наличием разрывных параметров в функциях жесткости оболочки. В связи с этим определились следующие направления:

1. Отыскание аналитических решений, например, в тригонометрических рядах с использованием дельта-функций, которые имеют импульсный характер и учитывают скачки и изломы в искомых функциях. Отметим, что в отличие от гладкой оболочки получаемая здесь система алгебраических уравнений для коэффициентов членов ряда разложения даже при шарнирном опирании оказывается совместимой в силу неортогональности тригонометрических функций дискретного аргумента при произвольных жесткостях и расположении ребер.

2. Рассмотрение ребристой оболочки как контактной задачи. При этом используется расчленение на гладкую оболочку и подкрепляющие ребра, либо выделяются гладкие панели и ребра, которые стыкуются между собой. Так, например, в оболочках с параллельной системой ребер, нормальных к двум шарнирно опертым сторонам, для каждого гладкого участка ищется решение в виде одинарных тригонометрических рядов с последующим выполнением условий контакта по линиям ребер. Здесь, как и вообще для аналитических решений, ограничения применимости метода обусловливаются трудностями выбора функций, удостоверяющих различным граничным условиям. Еще более усложняются аналитические методы решения при перекрестной системе ребер.

Применение методов численного анализа для расчета ребристых оболочек свободно от ряда недостатков, присущих аналитическим решениям. Метод численного решения позволяет учитывать различные контурные условия и условия сопряжения, наличие ребер и др.

Рассмотрим основные соотношения. Используя принцип минимума потенциальной энергии (принцип возможных перемещений Лагранжа)

(1)

Можно получить уравнение равновесия подкрепленной оболочки и статические граничные условия. В случае тонких оболочек деформации представляются в виде [ 1 ]

(2)

Компоненты с относятся к среднему слою. В случае пологих оболочек

(3)

, , – кривизны поверхности оболочки.

Подставляя выражения (2) (3) в (1) для упругого трехмерного тела и интегрируя по толщине оболочки в пределах от до получим векторное вариационное уравнение для гладких тонких упругих оболочек

, , – компоненты интенсивности общей внешней нагрузки на оболочку, - площадь срединной поверхности оболочки. Для пологой оболочки и следовательно , (рис.1)

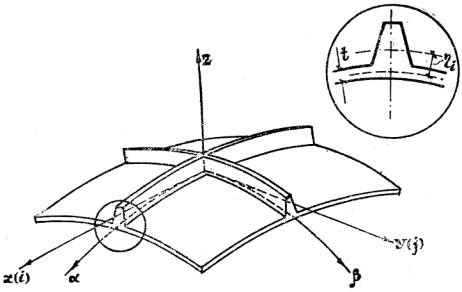
Рис.1

Здесь

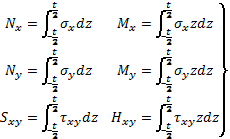
A и В – коэффициенты первой квадратичной формы срединной поверхности оболочки в криволинейных ортогональных координатах , . Принята зависимость, соответствующая обычным гипотезам тонких оболочек:

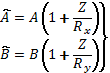
При интегралах вида в выражении (7) использовались упрощения 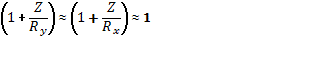. Учет этих членов привел бы к более точным выражениям для усилий (8), чем точность исходных предпосылок теории оболочек.

Из уравнения (4) в качестве чистого случая могут быть получены вариационные уравнения для криволинейных балок. Например, для криволинейных балок с осью , лежащей в плоскости , при учете энергий продольной деформации, кручения и изгиба в двух плоскостях получаем [1,2]

(5)

, , – компоненты интенсивности общей внешней нагрузки, приложенной к оси балки

(6)

- угол закручивания

Зависимости (6) приведены для случая криволинейной балки с осью OX

Аналогичные уравнения и зависимости будут для криволинейной балки с осью , лежащей в плоскости [2]

(7)

Где

(8)

Если балки являются ребрами, подкрепляющими оболочку (рис.1), то условия неразрывности деформаций между ребрами и оболочкой на основе гипотез прямых нормалей и ненадавливания волокон имеют вид:

(9)

Ребра расположены эксцентрично по отношению к ее срединной поверхности, h - расстояние от оси балки до срединной поверхности оболочки. Для ребер на внутренней поверхности оболочки величина берется со знаком «-».

Вариационное уравнение для тонкой упругой оболочки, подкрепленной ребрами i-того и j-того направлений будет иметь вид

Где , , – потенциальные энергии деформаций гладкой оболочки и ребер, , , - потенциал внешних сил, приложенных к гладкой оболочке и ребрам, m,n – число ребер соответственно i-того и j-того направлений

Данная сумма содержит в качестве слагаемых столько уравнений, сколько имеется ребер соответствующих направлений. Аналитическое решение состояния ребристых оболочек получено в простых случаях опирания, т.е. с граничными условиями типа Навье. В этом случае функции перемещений представляются в виде ряда Фурье [ 3,4 ] для решения практических задач с более сложными условиями закрепления необходимо применить численные методы. В настоящее время наиболее популярным является МКЭ [ 5-7]. Основные этапы решения которого являются: разбиение оболочечной конструкции на элементы; составление разрешающих уравнений с помощью метода начала возможных перемещений; определение узловыхперемещений, деформаций и напряжений. На основе этого метода с применением пакета прикладных программ Abaqus были получены результаты расчета серии подкрепленных оболочек.

Литература

1. Абовский Н.П. Ребристые оболочки: В 2-х т. - Красноярск: Изд-во Крас-нояр. политехн., ин-та, 1967

2.Абовский Н.П. Вариационные принципы теории упругости и теории оболочек. / Абовский Н.П., Андреев Н.П., Дерюга А.П.- М.: Наука, 1978. 228 с.

3. Амбарцумян С.А. Теория анизотропных пластин: Прочность, устойчивость и колебания. 2-е изд., перераб. и доп. - М.: Наука. Гл. ред. физ.-мат. лит., 1987.-360 с.

4. Амиро И.Я. Теория ребристых оболочек / Амиро И .Я., Заруцкий В.А. // Методы расчета оболочек: В 5-ти т. Т.2. Киев: Наук, думка, 1980. - 368 с.

5. Галлагер Р. Метод конечных элементов. Основы: Пер. с англ. — М.: Мир, 1984-428 С.

6. Зенкевич О. Метод конечных элементов в технике — М.: Мир, 1975.-542 С.

7. Сегерлинд Л. Применение метода конечных элементов — М.: Мир, 1979. — 392 С