T.R. Amanbayev¹, S.J. Antony²

¹State University of South Kazakhstan, Shymkent, Kazakhstan;

²University of Leeds, Leeds, UK

Dynamics of dual aggregate of particles in suspension

We consider the dynamics of interaction of two particles in suspension. The task of bringing together the particles in suspension is quite complex and interesting, because it happens on the distance at which the surface forces come into play. Usually the interaction at distances much smaller than radius of the particle is considered. In this case, as known, Stokes formula that determines the effect of viscous resistance of environment is unacceptable [1]. Formula for viscous resistance of particles at close distances can be obtained from the hydrodynamic analog of movement in plane capillary with Poiseuille’s flow in it [1,2]. After ignoring the minor terms it becomes as [1]

(1)

where h is the shortest distance between the surfaces of the particles, μ is dynamic viscosity of liquid, t is time, a is radius of particles. Sign “−“ in left side of equation (1) means, that force is directed against velocity of coming together of particles dh/dt. Note, that the expression (1) is valid for short distance between particles, i.e. when .

The force of molecular attraction of particles with short distances between them will be written as [1,3]

(2)

Here K is Van-der-Waals-Gamaker constant. Equation of motion of particles relative to another will be written in the form

(3)

where m is mass of particle. We choose following dimensionless variables: , , . Equation (3) in dimensionless variables takes the form

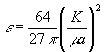, (4)

It is estimated that the coefficient at the higher derivative ε is small enough. For example, for suspension of water with particles with radius a<~10 μm at the normal conditions is ε<~. It means that equation (4) is singularly perturbed equation. Singular equation corresponding for equation (4) has the form

, () (5)

where is dimensionless relative velocity of particle. Equation (5) has the single solution

(6)

Since under common properties of singularly perturbed equations for very large times integral curve of equation (4) should be strived to relationship (6), it follows that the velocity of the particle at the limit for →0 tends to infinity. Note solution (6) is stable because . Integration of equation (5) gives

. (7)

It follows that the aggregation of two particles (=0) occurs during final time . In practice, strong enough fixation of particles is necessary that the distance of their surfaces is less than m [1]. Equation (4) cannot be integrated in finite form, therefore for integration this equation must be performed using numerical methods. For the convenience the equation (4) is written as a system

, . (8)

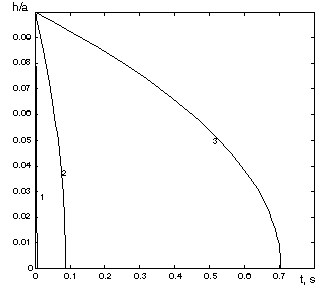
We want to solve this system with initial conditions: . Note that the value should be much less than one. In addition, to set the initial velocity of the particles need to know the previous history of the movement of particles relative to each other. On a random value (not of equal to value, satisfying condition (6)) velocity reaches the value corresponding solution (6). This figure shows the dynamics of aggregation of particle with a radius 2 μm (curve 1), 5 µm (2) and 10 µm (3). Dimensionless initial distance between particles is =0.1 and initial velocity satisfies to expression (6). Calculations showed that the numerical solution of system (8) is nearly identical to the solution (7) of singular equation.

Литература:

1. Бибик Е.Е. Реология дисперсных систем. – Ленинград. 1981.

2. Лойцянский Л.Г. Механика жидкости и газа. – Москва: Наука. 1970.

3. Волощук В.М., Седунов Ю.С. Процессы коагуляции в дисперсных системах. – Ленинград: Гидрометеоиздат. 1975.