Акимова В.А., д. ф.-м. н. Латышев А.В., д. ф.-м. н. Юшканов А.А.

Московский государственный областной университет, Москва

Решение задачи о поведении газа над движущейся

поверхностью

Задача о поведении газа над движущейся поверхностью в последние годы привлекает пристальное внимание [1]-[4]. Это связано с развитием современных технологий, в частности, технологий наноразмеров. В [1]-[4] эта задача решалась численными или приближенными методами. В настоящей работе показано, что эта задача допускает аналитическое решение. Аналитическое решение строится с помощью теории обобщенных функций и сингулярных интегральных уравнений.

Пусть разреженный одноатомный газ занимает полупространство над плоской твердой поверхностью, лежащей в плоскости . Поверхность совершает гармонические колебания вдоль оси по закону . Функция распределения газовых молекул описывается эволюционным - модельным кинетическим БГК – уравнением (см. [2] и [3]):

где – время между столкновениями молекул в газе, – равновесная функция распределения Максвелла, имеющая вид

,

где – масса молекулы, – постоянная Больцмана, – температура газа, которая считается постоянной в данной задаче.

Молекулы отражаются от стенки зеркально – диффузно с коэффициентом диффузности . Это означает, что ая часть молекул отражается диффузно, а остальная (1-) отражается зеркально. Для функции распределения имеем следующее граничное условие на стенке:

где - распределение Максвелла – Больцмана по скоростям вида

,

Вдали от стенки () функция распределения считается исчезающей: .

После линеаризации и обезразмеривания задачи приходим к следующему уравнению

, (1)

где - массовая скорость газа, имеющая вид

, ,

а функция связана с следующим соотношением .

Рассматривая аналогичную задачу, когда поверхность совершает колебания по закону , приходим к следующему кинетическому уравнению:

. (2)

Объединим два действительных уравнения (1) и (2) в одно комплекснозначное:

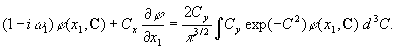
Граничные условия на функцию таковы:

, .

Далее, следуя Черчиньяни [5], введем неизвестную функцию () равенством Получим следующую граничную задачу:

, (3)

, (4)

. (5)

Разделение переменных в уравнении (3) осуществляется следующей подстановкой

(6)

где - параметр разделения, или спектральный параметр, вообще говоря, комплексный. Подставляя (6) в уравнение (3) получаем характеристическое уравнение

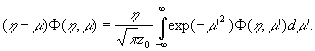(7)

Если ввести обозначение

(8)

то уравнение (7) можно переписать с помощью (8) в виде

(9)

Уравнение (9) является конечным (недифференциальным) уравнением. Условие (8) называется нормировочным условием, нормировочным интегралом, или просто нормировкой.

Решение характеристического уравнения будем искать в пространстве обобщенных функций [6]. Обобщенное решение уравнения (9) имеет вид:

(10)

когда . Здесь - произвольная непрерывная функция, определяемая из условия нормировки, – дельта-функция Дирака, символ означает главное значение интеграла при интегрировании . Подставляя (10) в (8), получаем уравнение, из которого находим где - дисперсионная функция, введенная равенством

Собственные функции (10) определены с точностью до мультипликативной «постоянной» :

Далее в силу однородности уравнения (3) можно считать, что Таким образом, собственные решения имеют вид

Далее будем рассматривать случай, когда дисперсионная функция нулей не имеет.

Составим общее решение уравнения (3) в виде интеграла по непрерывному спектру от собственных решений:

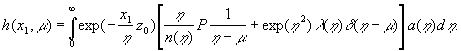(11)

Здесь - неизвестная функция, отвечающая непрерывному спектру.

Решение (11) можно представить в классическом виде:

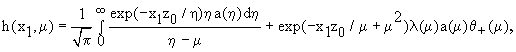(12)

где – функция Хэвисайда, и .

Доказательство проведем для случая диффузных граничных условий, то есть, положим, здесь . Очевидно, что разложение (12) автоматически удовлетворяет граничному условию (5) вдали от стенки. Подставим разложение (12) в граничное условие (5). Получаем одностороннее сингулярное интегральное уравнение с ядром Коши

.

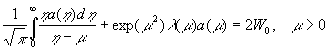Введем вспомогательную функцию

.

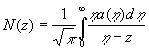Для этой функции выполняются формулы Сохоцкого:

, ,

.

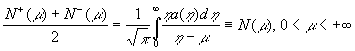Выпишем формулы Сохоцкого для дисперсионной функции:

,

, где .

Пользуясь этими формулами, приходим к краевому условию:

. (13)

Уравнение (13) – это краевое условие неоднородной краевой задачи Римана — Гильберта. Эта задача состоит в отыскании такой неизвестной функции , аналитической вдоль разрезанной плоскости положительной полуоси, граничные значения которой на берегах этого разреза удовлетворяют краевому условию (13). Рассмотрим соответствующую однородную краевую задачу Римана:

(14)

где

.

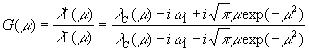Логарифмируя краевое условие (14), получаем:

(15)

Здесь означает регулярную ветвь логарифма, фиксированную в нуле условием . Отсутствие нулей дисперсионной функции означает, что приращение на полуоси равно нулю. Поэтому решение задачи о скачке (15) (при k = 0) дается через интеграл типа Коши:

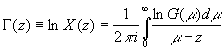; . (16)

Вернемся к решению неоднородной задачи (13), предварительно преобразовав с помощью (16) ее к виду:

(17)

С помощью однородной задачи (17) получим:

. (18)

Учитывая поведение всех входящих в краевое условие (18) функций в комплексной плоскости и в бесконечно удаленной точке получаем общее решение

. (19)

Согласно (19) искомая функция имеет вид . Потребуем, чтобы правая часть была исчезающей функцией в бесконечно удаленной точке. Разложим в ряд Лорана в окрестности бесконечно удаленной точки

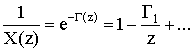, где .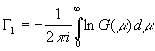

Таким образом, чтобы правая часть в бесконечно удаленной точке имела асимптотическое поведение, как , необходимо на наложить условие . Вспомогательная функция построена однозначно и имеет вид . Искомый неизвестный коэффициент непрерывного спектра находится из формулы Сохоцкого:

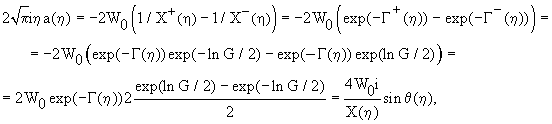
откуда

(20)

Формула (20) дает представление в явном виде коэффициента непрерывного спектра. На этом этапе доказательство разложения (11) (или (12)) закончено.

С помощью формулы (20) представим разложение (12) в явном виде:

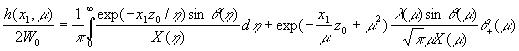. (21)

Равенство (21) означает, что искомая функция распределения построена в явном виде полностью, что и заканчивает аналитическое решение задачи.

Данная задача с зеркально-диффузными граничными условиями может быть решена методом, развитым в работах [7] – [9].

Литература

1. Sharipov F., Kalempa D. Gas flow around a longitudinally oscillations plate at arbitrary ratio of collision frequency to oscillation frequency. RGD, 25-th Int. Symp. Novosibirsk. 2007, 1140-1145.

2. Дудко В.В., Юшканов А.А., Яламов Ю.И. Влияние свойств поверхности на характеристики сдвиговых волн. ЖТФ. 2005. Т. 75, вып.4, 134-135.

3. Дудко В.В., Юшканов А.А., Яламов Ю.И. Генерация колеблющейся поверхностью сдвиговых волн в газе. ТВТ. 2009. Т. 47. №2, 262-268.

4. Дудко В.В. Скольжение разреженного газа вдоль неподвижных и колеблющихся поверхностей, дисс., Москва, 2010.

5. Черчиньяни К. Теория и приложения уравнения Больцмана, К. Черчиньяни – М.: Мир, 1978.

6. Жаринов В.В., Владимиров В.С. Уравнения математической физики, М.: Физмалит, 1999.

7. Латышев А.В., Юшканов А.А, Аналитические методы в кинетической теории, А.В. Латышев, А.А. Юшканов – Монография. Изд-во МГОУ, М., 2008, 280 с.

8. Latyshev A.V., Yushkanov A.A. Skin effect with arbitrary specularity in Maxwellian Plasma// J. of Math. Phys. 2010. V. 51, P. 113505-1-113505-10, pp. 10.

9. Latyshev A.V., Yushkanov A.A. Temperature jump in degenerate quantum gases with the Bogoliubov excitation energy and in the presence of the Bose – Einstein condensate // Theor. and Mathem. Physics, 165(1): 1359 – 1371 (2010).