ИССЛЕДОВАНИЕ АПРИОРНЫХ ОЦЕНОК
ВЫРОЖДАЮЩЕГОСЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
В
НЕОГРАНИЧЕННОЙ ОБЛАСТИ
ф.-м.ғ.к., доцент Рахимова Г.К.,
магистрант Канатбекова
Т.К.
Таразский государственный
университет
ТҮЙІН
Бұл жұмыста Гильберт кеңістігінде бір классты
сызықты теңдеулердің шешімдерінің бар болуы және
сонымен қатар шешімдерінің
тегістілігі мен аппроксимативтік қассиеттері зерттелген. Көрсетілген нәтижелерді зерттеу кезінде бір
классты нұқсанды
сызықты теңдеулердің
жартылай периодты Дирихле есебінің шексіз облыста априорлы
бағасы алынды. Келтірілген
зерттеулер гидромеханика, газдинамикасында, беттер және
қабықшалар теориясында
қолданылады.
SUMMARY
In work of Hylbert
space
the smooth and approximate properties of solutions of the one class linear functioning equations degenerated are
researched. Before research it of
coercive solutions of the high series one class degenerated equations of a
Dirichlet semi periodic problem necessary and sufficient conditions were
obtained. The carried researched can be used in hydro - mechanic, gas - dynamics and
surfaced and envelopes theory.
В ![]() рассмотрим следующую задачу:
рассмотрим следующую задачу:
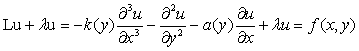 (1)
(1)
![]() (2)
(2)
где
![]() ,
,
![]() -класс функции
бесконечно дифференцируемых и финитных с носителями
-класс функции
бесконечно дифференцируемых и финитных с носителями ![]() .
.
Предположим, что коэффициенты уравнения (1) и весовая функция ![]() удовлетворяют
условиям :
удовлетворяют
условиям :
i) ![]() и
и ![]() - не убывают на отрезке
[0,1];
- не убывают на отрезке
[0,1];
ii) ![]() .
.
Основными
результатами являются следующие теоремы:
Теорема 1. Пусть выполнены условия і)-іі). Тогда оператор ![]() ограничен в
ограничен в ![]() в том и только в том
случае, если
в том и только в том
случае, если ![]()
![]() ,
,
где
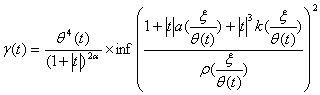 ,
,
а тут ![]() - любая функция, удовлетворяющая неравенству
- любая функция, удовлетворяющая неравенству
![]() , причем
, причем ![]() .
.
Теорема 2. Пусть выполнены условия і)-іі).
Тогда при ![]() для любого
для любого ![]() существует единственное решение и для него
справедлива оценка
существует единственное решение и для него
справедлива оценка
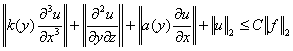 ,
,
где С- положительное постоянное
число.
Литература
1.
Кальменов Т.Ш., Отелбаев М. // Дифференциальные уравнения, 1977, т.13, №7, С. 1244-1255.
2.
Муратбеков М. Б. // Дифференциальные
уравнения, 1981, т.17, №5, С. 893-901.
3.
Кальменов Т.Ш., Отелбаев
М. О гладкости решений одного класса вырождающихся эллиптических уравнений //
Дифференциальные уравнения. –1977– Т.13. – № 7. – С.1244-1255.
4.
Муратбеков М.Б. О гладкости решений одного класса неравномерно
вырождающихся эллиптических уравнений // Известия АН Каз ССР. Сер.физ-мат. - 1981. - №5. - С.71-73.
5.
Муратбеков М.Б. О гладкости решений одного класса неравномерно
вырождающихся эллиптических уравнений высокого порядка // Корректные краевые
задачи для неклассических уравнений математической физики. - Новосибирск. - 1981. - С.144-146.