МАТЕМАТИКА / 4.Прикладная математика

Стрюков Р.К.

Воронежский Государственный Университет, Россия

Сходство на основе нечеткого моделирования

Пусть каждый объект в нашей предметной области представлен N-мерным вектором, т.е.

таким образом, что это i-ый признак . Признаки могут быть из любой области т.е.. Например, признаки могут быть целые числа, вещественные числа и символы из некоторого дискретного набора значений. Область признаков i может отличаться от области признаков j. Также допустимо, что значение признака не определено или отсутствует [1].

Пусть обозначает множество рассматриваемых объектов, такие, что объекты, , . Например, может представлять некоторый неизвестный объект, личность которого устанавливается, в то время как принадлежит к базе данных известных объектов. В этой статье рассматривается мера сходства, которая основывается на расстоянии объектов и , и особенностей объекта и . Чем меньше расстояние между объектами, тем больше их сходство и наоборот. Для того, чтобы измерить расстояние между парой признаков, и , , введем нечеткие лингвистические переменные расстояния i-го компонента . Эта нечеткая лингвистическая переменная состоит из нескольких нечетких множеств , которые определены на . Всякий раз, когда и не определены, все не определены также.

В общем случае, нечеткие множества , которые представляют расстояние i-й функции, будет отличаться от нечетких множеств, представляющих расстояние j-й функции, в зависимости от характера функций [2]. Другими словами,

По определению, для каждого , предполагаем, упорядочение

на нечетких множествах, такое, что расстояние признака i, соответствующее нечеткому множеству соответствует большее расстояние, чем нечеткому множеству , . Формально для каждой пары нечетких множеств и , , требуем существование разбиения на два непересекающихся подмножества и таких, что выполнены следующие условия:

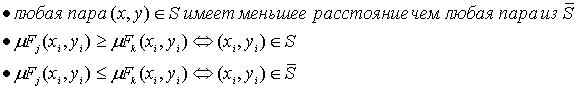
Кроме того, требуем, чтобы достигало своего максимального значения, если и идентичны, т.е.

Для некоторых приложений требуется выполнение ,

Для моделирования глобального сходства объектов, вводим нечеткую лингвистическую переменную расстояние объектов и , или для краткости [3]. состоит из нескольких нечетких множеств, определенных на интервале [0,1]. Пусть обозначим базовую переменную лингвистической переменной . Функции принадлежности нечетких множеств имеют вид

Аналогично, предполагаем, упорядочение на

таким образом, что представляет собой большее расстояние между и , чем,. Формально, требуем для каждой пары нечетких множеств и, существование вещественного числа, , которое делит диапазон [0, 1] базовой переменной u на два интервала [0, I] и [I, 1], такое что

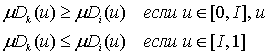
Чем меньше значение , тем меньше расстояние между и . Случаи и , представляют собой наименьшее и наибольшее возможные расстояния (т.е. наибольшую и наименьшую степени сходства), соответственно. Аналогично, требуем

С учетом лингвистических переменных и , расстояние между векторами и , определяется с помощью правил [4]. Общий формат правила

если сходство признака есть и/или

сходство признака есть и/или

…

сходство признака есть

То сходство и есть

или, более формально

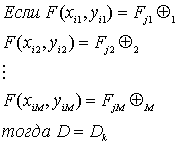
где каждый обозначает либо 'и' или 'или' связку.

Правила такого вида обеспечивают очень гибкую модель и позволяют эксперту, выразить свои знания о некоторой предметной области.

После определения сходства двух признаков, могут быть использованы стандартные методы вывода, для того чтобы сделать заключение о схожести двух заданных объектов и .

Литература:

1. A. Kandel. Fuzzy Mathematical Techniques with Applications.-Addison Wesley, 1986.

2. Малышев Н.Г. Нечеткие модели для экспертных систем в САПР / Малышев Н.Г., Берштейн Л.С., Боженюк А.В. –М.: Энергоатомиздат, 1991

3. Кофман А. Введение в теорию нечетких множеств: Пер. с франц.–М.: Радио и связь, 1982.

4. Татаркин Д.С. Математическое и программное обеспечение механизма логического вывода в нечетких продукционных системах. -Воронеж. 2007.