ДИРИХЛЕ ЕСЕБІНІҢ ШЕШІМІНІҢ БАР БОЛУЫНЫҢ ЗЕРТТЕУІ
ф.-м.ғ.к., доцент Рахимова Г.Қ.
Тараз мемлекеттік университеті
Жумалиева Л.Д.
Абай атындағы қазақ
ұлттық педагогикалық университеті
Садуақасова С.Н.
Тараз инновациялық гуманикалық
университеті
РЕЗЮМЕ
В
работе рассматриваются существование, гладкость решении вырождающихся уравнении одного класса в
пространстве ![]() . При
изучении полученных результатов, сформулировали необходимые и
достаточные условия аппроксимативных свойств полупериодических задач Дирихле
для нелинейных вырождающихся уравнений. Были исспользованы методы изучения
спектральных свойств дифференциальных операторов. Новый метивод получения теорем вложения. Установлены спектральные
характеристики и гладкость решения уравнений. Двусторонние оценки поперечников
по Колмогорову вложения и аппроксимативных чисел оператора вложения и критерий
принадлежности оператора вложения классам. Найдена двусторонняя асимптотика.
. При
изучении полученных результатов, сформулировали необходимые и
достаточные условия аппроксимативных свойств полупериодических задач Дирихле
для нелинейных вырождающихся уравнений. Были исспользованы методы изучения
спектральных свойств дифференциальных операторов. Новый метивод получения теорем вложения. Установлены спектральные
характеристики и гладкость решения уравнений. Двусторонние оценки поперечников
по Колмогорову вложения и аппроксимативных чисел оператора вложения и критерий
принадлежности оператора вложения классам. Найдена двусторонняя асимптотика.
SUMMARY
There are ![]() space the smooth of solutions of the one class functioning equations
degenerated are researched. Before research it of coercive solutions of the
high series one class no linear
degenerated equations of a Dirichlet semi periodic problem necessary and
sufficient conditions were obtained. Developed methods for studying the
spectral properties of differential operators. A new method of proving
embedding theorem which is. Investigated spectral characteristics and
smoothness of solutions to equations. Two-sided estimates for Kolmogorov`s
width and for the approximation numbers of an embedding operator, and a criterion for belonging of an embedding operator
to the classes. The found of two-sided asymptotes.
space the smooth of solutions of the one class functioning equations
degenerated are researched. Before research it of coercive solutions of the
high series one class no linear
degenerated equations of a Dirichlet semi periodic problem necessary and
sufficient conditions were obtained. Developed methods for studying the
spectral properties of differential operators. A new method of proving
embedding theorem which is. Investigated spectral characteristics and
smoothness of solutions to equations. Two-sided estimates for Kolmogorov`s
width and for the approximation numbers of an embedding operator, and a criterion for belonging of an embedding operator
to the classes. The found of two-sided asymptotes.
Дифференциалды
теңдеулерді зерттеу кезінде көбіне көңіл
бөлінетін сұрақтар мынадай: шешімнің бар болуы,
жалғыздығы, олардың қасиеттері. Дифференциалды
теңдеудің шешімінің бар болуы және
жалғыздығы шарты нақты жүріп жатқан процестің
сипаттауының қажетті шарты болып табылады. Сондықтан
сызықты және сызықты емес дифференциалды теңдеулер
теориясындағы маңызды мәселенің бірі ретінде
олардың шешімінің бар болуы мен жалғыздығы болып
табылады.
Соңғы жылдары нұқсанды теңдеулер өте
қарқынды зерттелуде, себебі олардың қолданбалы
маңыздылығы артқан (газдық динамика, гидромеханикада
және моментсіз қабықшалар теориясындағы есептер,
ңұқсанды теңдеулерді зерттеудің
қажеттілігін туындайды). Сызықты дифференциалдық
теңдеудің шешімінің бар болуын дәлелдеу мәселесі
көптеген ғалымдардың жұмыстарында
қарастырылған: С.М. Никольский [1], П.И. Лизоркин және С.М.
Никольский [2-3], М.М. Смирнов [4], А.В. Бицадзе [5], М.И. Вишик және
В.В. Грушин [6], В.П.Глушко [7-8],
Т.Ш.Кальменов және М. Отелбаев [9], М.Б.Муратбеков [10-13] және
басқа да авторлар.
Жоғарғы ретті
сызықты дифференциалдық теңдеудің шешімінің бар
болуын зерттеген ғалымдар Ю.А.Дубинский, В.К. Романко, Н.И. Юрчук, С.Я.
Якубов, В.П. Михайлов, С.Г. Пятков
және т.б.
Зерттеу жұмысын біз
жоғарғы ретті дифференциалдық теңдеуге жүргіздік.
Берілген W={(х,у):0<x<2p, 0<y<1} облысында төмендегі сызықты
емес дифференциалдық теңдеуді
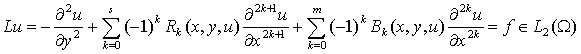 , (1)
, (1)
мынадай шектік шарттармен
бірге қарастырамыз:
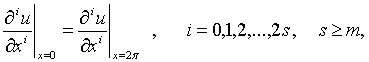 (2)
(2)
![]() (3)
(3)
Мұнда ![]() .
.
Барлық жерде (1)
теңдеудің коэффиценттерін төмендегі шектеулер қоямыз:
![]() бөлікті-үздіксіз функциялар
және берілген аргументтері бойынша төмендегі шарттарды
қанағаттандырады:
бөлікті-үздіксіз функциялар
және берілген аргументтері бойынша төмендегі шарттарды
қанағаттандырады:
![]()
![]() , А-кез-келген
белгіленген сан ;
, А-кез-келген
белгіленген сан ;
![]()
![]() , А-кез-келген белгіленген сан, мұнда
, А-кез-келген белгіленген сан, мұнда ![]() функцияларын сәйкесінше
функцияларын сәйкесінше ![]() -
-![]() шарттарын қанағаттандырады.
шарттарын қанағаттандырады.
![]()
![]() .
. ![]()
![]()
1
Негізгі алынған нәтиже
Теорема 1 Айталық а)-б) шарттары орындалсын, онда кез –келген
fÎL2 үшін (1)-(3)
есібінің L2(Ώ) кеңістігінде жататын шешімі бар болады және ол
төмендегі теңсіздікті қанағаттандырады
![]() , (
, ( ![]() ), (4)
), (4)
мұндағы С>0, ![]() – бекітілген тұрақты сандар.
– бекітілген тұрақты сандар.
2 Қосымша дәлелдеулер
Төмендегі есепті
қарастырайық:
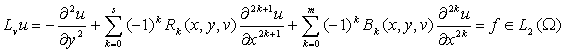 , (5)
, (5)
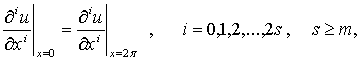 (6)
(6)
![]() (7)
(7)
Лемма 1 Айталық ![]() және а)-б) шарттары орындалсын, онда кез –келген
fÎL2 үшін (5)-(7)
есібінің L2(Ώ) кеңістігінде жататын жалғыз шешімі бар болады және ол
үшін төмендегі баға
орындалады:
және а)-б) шарттары орындалсын, онда кез –келген
fÎL2 үшін (5)-(7)
есібінің L2(Ώ) кеңістігінде жататын жалғыз шешімі бар болады және ол
үшін төмендегі баға
орындалады:
![]() (8)
(8)
мұндағы ![]() ,
C>0 - u, v функцияларына тәуелсіз.
,
C>0 - u, v функцияларына тәуелсіз.
Дәлелдеуі. Айталық
![]() .
.
Онда (5)-(7) есебіміз (1)-(3) есебіне
сәйкес келеді, мұндағы ![]() функциялары,
сәйкесінше
функциялары,
сәйкесінше ![]() функцияларымен
ауыстырылған. Және бұл жағдайда,
функцияларымен
ауыстырылған. Және бұл жағдайда, ![]() функциялары үшін
а)-б) шарттары орындалғанда [13] жұмысағы теоремадан
лемманың дәлелдеуін аламыз. Олай болса, (1)-(3) есебінің жалғыз шешімі
функциялары үшін
а)-б) шарттары орындалғанда [13] жұмысағы теоремадан
лемманың дәлелдеуін аламыз. Олай болса, (1)-(3) есебінің жалғыз шешімі ![]() бар болады және ол (8) бағаны қанағаттандырады.
Демек, егер
бар болады және ол (8) бағаны қанағаттандырады.
Демек, егер ![]() , онда
, онда ![]() . Сонымен
қатар,
. Сонымен
қатар, ![]() (2.1)-(2.3) есебінің шешімі
болғандықтан, кез- келген
(2.1)-(2.3) есебінің шешімі
болғандықтан, кез- келген ![]() функциясы үшін
функциясы үшін ![]() аламыз. Сол себепті, (5)-(7) шектік есептің шешімінің
бар болуы,
аламыз. Сол себепті, (5)-(7) шектік есептің шешімінің
бар болуы, ![]() кеңістігіндегі
кеңістігіндегі
![]() операторының
қозғалмайтын нүктесі бар болуымен эквивалентті,
яғни
операторының
қозғалмайтын нүктесі бар болуымен эквивалентті,
яғни ![]() функциясының бар болуы және ол
функциясының бар болуы және ол ![]() арқылы өрнектеледі. Мұнда
арқылы өрнектеледі. Мұнда ![]() сәйкес
сәйкес ![]()
Олай болса, (5)-(7)
есебінің шешімі бар болса, ![]() операторының қозғалмайтын нүктесі бар. Осы мақсатпен атақты Шаудер принципін қолданамыз.
операторының қозғалмайтын нүктесі бар. Осы мақсатпен атақты Шаудер принципін қолданамыз.
Айталық ![]() -
кеңістігінде шар берілсін
-
кеңістігінде шар берілсін ![]() – және А- кез-келген оң сан.
– және А- кез-келген оң сан.
Лемма 2 Айталық а)-б) шарттары
орындалсын, онда ![]() жиыны
өзіне-өзін бейнелейтін оператор
жиыны
өзіне-өзін бейнелейтін оператор ![]() .
.
Дәлелдеуі
Бұл
лемманың дәлелдеуі 1 леммасынан тікелей ала аламыз, егер А санын ![]() деп алсақ және (8) бағасын
ескерсек.
деп алсақ және (8) бағасын
ескерсек.
Айталық ![]() –
– ![]() шарының керібейнесі.
шарының керібейнесі.
Пайдаланылған әдебиеттер
тізімі:
1. Никольский С.М. Вариационная проблема для уравнения эллиптического типа вырождением на границе // Труды Мат. Ин-та АН СССР. – Москва - 1979. - Т. 150, - С.212-238.
2. Лизоркин П.И., Никольский С.М.Эллиптические уравнения с вырождением. Дифференциальные свойства решений // Доклад АН СССР. – Москва - 1981. -Т.257. - №1. - С.42-45.
3. Лизоркин П.И., Никольский С.М.Эллиптические уравнения с вырождением. Дифференциальные свойства решений // Доклад АН СССР. -Москва - 1981. - Т.257. - №2. - С.278-282.
4. Смирнов М.М. Вырождающиеся эллиптические и гиперболические уравнения. - Москва: – 1966. -С.292.
5. Бицадзе А.В. Уравнения смешанного типа. Москва: - 1970. – С.164.
6. Вишик М.И., Грушин В.В. Краевые задачи для эллиптических уравнений вырождающихся на границе области // Матем. сб. – Моска – 1969. –Т.80. – №4. – С.455-491.
7.
Глушко В.П. Коэрцитивность в ![]() общих граничных
задачах для вырождающегося эллиптического уравнения второго порядка //
Функциональный анализ и его приложения. - Москва – 1968. – С.87-88.
общих граничных
задачах для вырождающегося эллиптического уравнения второго порядка //
Функциональный анализ и его приложения. - Москва – 1968. – С.87-88.
8. Глушко В.П. О гладкости решений вырождающихся дифференциальных уравнений в банаховом пространстве // Доклад АН СССР. - Москва –1971. – Т.148. – №1. – С.235-246.
9. Кальменов Т.Ш., Отелбаев М. О гладкости решений одного класса вырождающихся эллиптических уравнений // Дифференциальные уравнения. - Москва –1977– Т.13. – № 7. – С.1244-1255.
10. Муратбеков М.Б. Коэрцитивные оценки для одного дифференциального оператора высшего порядка // Дифференциальные уравнения. –Москва –1981– Т.17. – № 5. – С.893-901.
11. Муратбеков М.Б. О гладкости решений одного класса неравномерно вырождающихся эллиптических уравнений // Известия АН Каз ССР. Сер.физ-мат.-Алматы - 1981. - №5. - С.71-73.
12. Муратбеков М.Б. О гладкости решений одного класса
неравномерно вырождающихся эллиптических уравнений высокого порядка //
Корректные краевые задачи для неклассических уравнений математической физики. - Новосибирск - 1981. - С.144-146.
13. Муратбеков М.Б. О гладкости решений вырождающихся эллиптических уравнений и одномерного нелинейного стационарного уравнения Шредингера //Автореферат дисс. канд. Алматы. -1982. -С.16.