Аманбаев Т.,
Каналова М., Амантай Д.
Южно-Казахстанский
университет имени М.Ауэзова, Казахстан
МОДЕЛИРОВАНИЕ И РАСЧЕТ ПРОЦЕССА ВСПЛЫТИЯ ФЛОТАЦИОННОГО
КОМПЛЕКСА ПУЗЫРЕК-ЧАСТИЦЫ
Для обогащения материалов методом флотации
недостаточно одного факта закрепления гидрофобных частиц на пузырьках воздуха,
т.е. образования флотационного комплекса пузырек-частицы.
Полученный агрегат должен в определенных условиях всплывать к поверхности,
испытывая при этом воздействие гидродинамических потоков в камере машины, столкновения
и захват движущихся навстречу других частиц и т.п. Поэтому всплывание
флотационных комплексов пузырек-частицы является одним из важных этапов
процесса флотации.
Рассмотрим движение одиночного пузырька в
жидкости в условиях минерализации (заполнения частицами) его поверхности. При
этом будем считать, что пузырек и частицы имеют сферическую форму. Далее
нижними индексами l, b и p отмечены параметры соответственно
жидкости, пузырька и частиц суспензии.
Основные
уравнения. Уравнение для массы флотокомплекса
имеет вид
![]() , (1)
, (1)
где ![]() – масса
флотокомплекса; t – время, j –
интенсивность захвата частиц пузырьком. Запишем уравнение движения
флотокомплекса для одномерного случая
– масса
флотокомплекса; t – время, j –
интенсивность захвата частиц пузырьком. Запишем уравнение движения
флотокомплекса для одномерного случая
![]() , (2)
, (2)
![]() ,
, ![]() ,
, ![]() .
.
Здесь и далее ![]() – скорость
флотокомплекса;
– скорость
флотокомплекса; ![]() – скорость попадания
частиц на поверхность пузырька, которую в первом приближении можно принять
равной скорости движения частиц
– скорость попадания
частиц на поверхность пузырька, которую в первом приближении можно принять
равной скорости движения частиц ![]() (
(![]() =
=![]() );
); ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() – силы сопротивления, тяжести, Архимеда, Бассэ и
присоединенных масс соответственно, действующие на флотокомплекс при всплытии [1,2];
– силы сопротивления, тяжести, Архимеда, Бассэ и
присоединенных масс соответственно, действующие на флотокомплекс при всплытии [1,2]; ![]() ,
, ![]() ,
,![]() – объем, масса и диаметр пузырька;
– объем, масса и диаметр пузырька; ![]() ,
,![]() – масса и число частиц, осевших на поверхность пузырька;
– масса и число частиц, осевших на поверхность пузырька; ![]() ,
, ![]() – масса и диаметр
частицы; d – характерный размер флотокомплекса;
– масса и диаметр
частицы; d – характерный размер флотокомплекса; ![]() ,
,![]() – плотность и вязкость жидкости;
– плотность и вязкость жидкости; ![]() – плотность газа в
пузырьке;
– плотность газа в
пузырьке; ![]() – ускорение силы
тяжести. В
качестве характерного размера флотокомплекса можно взять его эффективный по
объему диаметр
– ускорение силы
тяжести. В
качестве характерного размера флотокомплекса можно взять его эффективный по
объему диаметр ![]() .
.
Наличие
закрепившихся на поверхности пузырька частиц приводит к увеличению силы
сопротивления пузырька со стороны жидкости. В данном случае учет этой
дополнительной силы осуществляется путем использования вместо диаметра пузырька
в силе взаимодействия эффективного диаметра (например, по объему
флотокомплекса).
К уравнениям
(1), (2) следует добавить уравнение, определяющее положение флотокомплекса
![]() . (3)
. (3)
Для системы
уравнений (1)–(3) поставим следующие начальные
условия ![]() . Если масса пузырька постоянна
. Если масса пузырька постоянна ![]() , то уравнение (1) переходит в уравнение для
, то уравнение (1) переходит в уравнение для ![]() . Далее рассмотрим случай покоящейся жидкости с частицами,
оседающими с постоянной скоростью
. Далее рассмотрим случай покоящейся жидкости с частицами,
оседающими с постоянной скоростью
![]() .
.
В этом случае ![]() .
.
Учет
минерализации поверхности пузырька.
По мере всплытия пузырька его поверхность постепенно минерализуется, т.е.
заполняется частицами. Отметим некоторые характерные особенности минерализации
поверхности пузырька при флотации. Закрепившиеся на пузырьках частицы занимают
часть его поверхности, уменьшая этим вероятность столкновения других частиц со
свободными участками поверхности пузырьков. Многочисленные опыты по флотации
свидетельствуют о том, что частицы закрепляются при столкновениях с верхней
полусферой поднимающегося пузырька, а затем потоком обтекающей пузырек жидкости
быстро сносятся на его нижнюю полусферу и тем самым слабо влияют на
столкновение других частиц со свободной поверхностью пузырька. Поэтому степень
минерализации пузырьков, определяемая концентрацией флотируемых частиц в
суспензии, начинает снижать скорость флотации при значениях, превышающих 50%.
Учитывая эти обстоятельства, здесь
предлагается следующая схема, приближенно учитывающая влияние заполнения
частицами поверхности пузырька на интенсивность захвата дисперсной фазы
пузырьком. В рамках принятых
предположений степень заполнения поверхности пузырька характеризуется высотой h шарового
сегмента, боковая поверхность которого покрыта частицами. Если
![]() , то эффективное сечение столкновения частиц с пузырьком
равно
, то эффективное сечение столкновения частиц с пузырьком
равно ![]() , а если
, а если ![]() , то, учитывая допущение о том, что частицы закрепляются
только на свободной поверхности пузырька, для
эффективного сечения имеем
, то, учитывая допущение о том, что частицы закрепляются
только на свободной поверхности пузырька, для
эффективного сечения имеем
![]() . Таким образом, выражение для интенсивности столкновения
частиц с пузырьком с учетом влияния степени минерализации поверхности пузырька
можно записать в виде
. Таким образом, выражение для интенсивности столкновения
частиц с пузырьком с учетом влияния степени минерализации поверхности пузырька
можно записать в виде
![]() ,
, 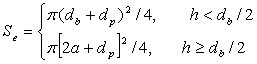 ;
; ![]() . (4)
. (4)
Здесь ![]() ,
, ![]() – эффективности
столкновений частиц с пузырьком, учитывающие эффекты зацепления и сноса частиц из-за силы
тяжести [2, 3]. Для определения величины h предположим, что поверхность пузырька покрывается
монослоем частиц в виде плотной упаковки. Выделим два определенных случая:
когда центры частиц образуют кубическую (наименее плотную) и тетраэдрическую
(наиболее плотную) решетки, полагая, что реальные расположения являются
промежуточными между указанными крайними ситуациями. Объемные доли, занимаемые
частицами
– эффективности
столкновений частиц с пузырьком, учитывающие эффекты зацепления и сноса частиц из-за силы
тяжести [2, 3]. Для определения величины h предположим, что поверхность пузырька покрывается
монослоем частиц в виде плотной упаковки. Выделим два определенных случая:
когда центры частиц образуют кубическую (наименее плотную) и тетраэдрическую
(наиболее плотную) решетки, полагая, что реальные расположения являются
промежуточными между указанными крайними ситуациями. Объемные доли, занимаемые
частицами ![]() и свободного
пространства между частицами
и свободного
пространства между частицами ![]() , для указанных крайних ситуаций определяются как [1]
, для указанных крайних ситуаций определяются как [1]
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Для любого периодического расположения
центров, характеризуемого параметрами ![]() и
и ![]() , при концентрациях частиц
, при концентрациях частиц ![]() из соображений
подобия следует
из соображений
подобия следует
![]() ,
, ![]() ,
,
причем для кубического расположения центров ![]() , а для тетраэдрического имеем
, а для тетраэдрического имеем ![]() . Тогда для любого промежуточного расположения частиц,
учитывая близость предельных значений
. Тогда для любого промежуточного расположения частиц,
учитывая близость предельных значений ![]() и
и ![]() , а также
, а также ![]() и
и ![]() можно использовать
аппроксимацию со средним значением коэффициента b и средним значением концентрации
можно использовать
аппроксимацию со средним значением коэффициента b и средним значением концентрации ![]() при плотной упаковке
[4]
при плотной упаковке
[4]
![]() ,
, ![]() ,
, ![]() . (5)
. (5)
Далее составим очевидное приближенное
соотношение ![]() , где
, где ![]() ,
, ![]() – свободная (от
частиц) и полная поверхность пузырька,
– свободная (от
частиц) и полная поверхность пузырька, ![]() ,
, ![]() – часть поверхности,
занятая частицами и средняя свободная поверхность между ними. Величина
– часть поверхности,
занятая частицами и средняя свободная поверхность между ними. Величина ![]() приближенно равна
сумме миделевых сечений частиц, а для величины
приближенно равна
сумме миделевых сечений частиц, а для величины ![]() воспользуемся
вышеприведенной аппроксимацией (5):
воспользуемся
вышеприведенной аппроксимацией (5): ![]() . Тогда для высоты шарового сегмента пузырька, занятого
частицами получим [5]
. Тогда для высоты шарового сегмента пузырька, занятого
частицами получим [5]
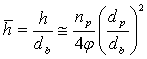 ,
, ![]() ,
, 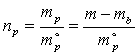 .
.
 Анализ результатов расчета. В качестве примера рассмотрим процесс всплытия воздушного пузырька в
воде при нормальных условиях. Значения определяющих параметров следующие:
высота колонны с водой Н=2 м, диаметр
частиц в суспензии
Анализ результатов расчета. В качестве примера рассмотрим процесс всплытия воздушного пузырька в
воде при нормальных условиях. Значения определяющих параметров следующие:
высота колонны с водой Н=2 м, диаметр
частиц в суспензии ![]() мкм, их истинная и
приведенная плотности
мкм, их истинная и
приведенная плотности ![]() кг/м3,
кг/м3, ![]() кг/м3
(объемная доля частиц в суспензии
кг/м3
(объемная доля частиц в суспензии ![]() ). В качестве характерных величин приняты следующие
параметры: установившаяся скорость всплытия U≡
). В качестве характерных величин приняты следующие
параметры: установившаяся скорость всплытия U≡![]() , высота слоя жидкости H, время H/U, начальная масса пузырька
, высота слоя жидкости H, время H/U, начальная масса пузырька ![]() . После приведения к безразмерному виду система уравнений (1)–(3)
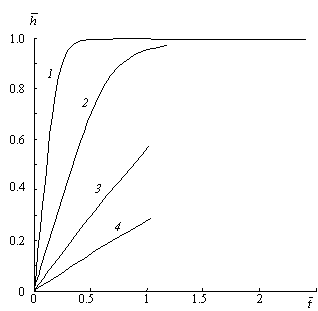
с замыкающими соотношениями (4), (5) интегрировалась численным методом. На рисунке
показано изменение степени заполнения поверхности пузырька частицами в зависимости
от безразмерного времени. Кривые 1–4 соответствуют разным начальным диаметрам
пузырька
. После приведения к безразмерному виду система уравнений (1)–(3)
с замыкающими соотношениями (4), (5) интегрировалась численным методом. На рисунке
показано изменение степени заполнения поверхности пузырька частицами в зависимости
от безразмерного времени. Кривые 1–4 соответствуют разным начальным диаметрам
пузырька ![]() , 250, 500 и 1000 мкм. Видно, что для пузырьков диаметром
менее 250 мкм их поверхность успевает почти полностью покрыться частицами до всплытия.
Причем для пузырьков диаметром
, 250, 500 и 1000 мкм. Видно, что для пузырьков диаметром
менее 250 мкм их поверхность успевает почти полностью покрыться частицами до всплытия.
Причем для пузырьков диаметром ![]() мкм это происходит
задолго до всплытия, что является не очень эффективным с точки зрения
оптимального использования высоты колонны. В этом смысле оптимальной является
использование пузырьков диаметром порядка 250 мкм, так как их поверхность
полностью минерализуется ближе к моменту всплытия.
мкм это происходит
задолго до всплытия, что является не очень эффективным с точки зрения
оптимального использования высоты колонны. В этом смысле оптимальной является
использование пузырьков диаметром порядка 250 мкм, так как их поверхность
полностью минерализуется ближе к моменту всплытия.
Литература
1.
Нигматулин Р.И. Основы
механики гетерогенных сред. – М.: Наука, 1978.
2. Теория и технология флотации руд. Под ред. О.С. Богданова. – М.: Недра, 1990.
3.
Yoon R.H., Luttrell G.H. The effect of bubble size on fine particle
flotation. Miner. Process. Extr. Metal. Rev. – 1989. – № 5. – Р. 101-112.
4.
Гольдштик М.А. Процессы
переноса в зернистом слое. –Новосибирск: ИТФ, 1984.
5.
Аманбаев Т.Р., Энтони С.Д. Моделирование
всплытия пузырька в жидкости с учетом минерализации его поверхности // Журнал
РАН. Теор. основы хим. технологии. – 2011. – Т. 45. – №5. – С. 687-695.