УДК 681.586
датчики больших
линейных перемещений для
информационно-измерительных
систем управления
Фирудин
Ибрагим оглы Мамедов , член
корр. НАН Азербайджана, д.т.н., профессор
Рена
Бахрам кызы Дадашева , к.т.н.,
доцент
Рамиз Агали оглы Гусейнов Р.А., к.т.н., доцент, ramiz_hu@mail.ru
Сумгаитский
Государственный Университет (СГУ)
Рена
Шариф кызы Асадова , к.т.н.,
доцент , Renaasadova2007@rambler.ru
Институт Систем Управления (ИСУ) НАНА
Шафагат
Тельман кызы Мамедова, докторант, shafa0977@gmail.com, СГУ
Гидаятзаде
Саяря Гисматали кызы, докторант, ИСУ,
Азербайджан
Для обеспечения требований к
надежности, качеству и экономической эффективности элементов систем управления,
требуются новые разработки в области информационной измерительной и
вычислительной техники. Значительное внимание при этом уделяется разработке
электромагнитных датчиков систем управления. Для измерения больших линейных
перемещений, авторы статьи создали датчик, проведен расчет и построена
характеристика рассмотренного датчика. Датчик может быть применен в
информационно-измерительных системах и в управлении технологическими процессами
в различных областях промышленности.
Ключевые слова: система управления, информационная
измерительная и вычислительная техника, электромагнитные датчики, линейное
перемещение
1.
Введение. Все
возрастающие требования к надежности, качеству и экономической эффективности
элементов систем управления, информационной измерительной и вычислительной
техники требуют новых разработок и широкий фронт поисковых исследований,
которые ведутся в этой области.
Значительное внимание при этом уделяется разработке
электромагнитных датчиков систем управления, отличающихся по простоте
эксплуатации, технологии изготовления и недорогих по стоимости.
2.
Постановка задачи. Как известно, общим звеном для большинства устройств систем управления
информационно-измерительной и вычислительной техники являются датчики,
преобразующие неэлектрические величины измерительных датчиков (усилия давления
и др.) в электрическую.
Разработчики, проектируя такие датчики на различные
диапазоны контролируемых перемещений, не могут существенно изменять поперечные
габариты датчика, а их продольные размеры находятся в прямой зависимости от
диапазона измеряемых перемещений. Для любого диапазона измерения созданный
датчик должен отвечать параметра ГОСТА ГСП. Поэтому каждому диапазону перемещений
требуется создание определенных конструкций датчиков, обеспечивающих в своем
диапазоне оптимальные соотношения габаритных размеров. Большие трудности стоят
при создании датчика больших перемещений, от 0,05м и выше. Существующие датчики
больших перемещений обладают весьма сложной конструкцией [1, 2].
3.
Методы решений. Для измерения больших линейных перемещений авторы
создали датчик, представленный на рис.3.1.
Как видно из рис.3.1, датчик состоит из магнитопровода
- 1, с обмотками возбуждения – 2, намотанными на этом магнитопроводе;
магнитопровода - 3 с системой - 4, состояшей из секций в количестве от 1 до n, измерительных обмоток.
Магнитопроводы изготавливаются из сплошной конструкционной стали.
Магнитопроводы 3 размещаются в зазоре 7 магнитопровода
1, имеет плоскую форму, на нижней и верхней плоскостях которого, в неглубоких
пазах, размещены секции обмоток измерительной системы -4. Обмотки системы
соединены между собой согласно последовательно и в точках соединения производят
ток разветвления через сопротивление 5 в общую точку 6. Длина сердечника
магнитопровода -1 берется равной b, а ширина – а, которая одновременно является толщиной магнитопровода 1.
Секции измерительных обмоток распределены по длине
магнитопровода 3, которая соответствует диапазону измеряемого перемещения X.
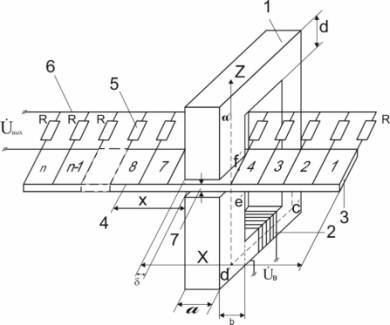
Рис.1 Магнитная система
датчика
Датчик работает следующим образом. При включении
обмотки возбуждения в сеть, в магнитопроводе 1 создается замкнутый магнитный
поток
Подвижным элементом, по необходимости, может быть либо
магнитопровод 1, (вдоль измеряемой величины X неподвижного магнитопровода 3) либо магнитопровод 3
(магнитопровод 1 останется неподвижным, а магнитопровод 3 перемещается по
диапазону измеряемой величины X).
Предполагаем, что подвижным элементом является магнитопровод 1. При этом
магнитопровод 1 связан с технологическим объектом, осуществляющим механическое
линейное перемещение, которое подлежит измерению.
В процессе работы датчика, исходное положение берется
равным секции 1. Относительно секции 1 магнитопровод получает перемещение X и положение магнитопровода
становится X+а. Выходная
величина датчика снимается из зажима крайнего сопротивления. Это напряжение
обозначим через 
. Каждая секция измерительного
магнитопровода пронизывается магнитным потоком, который создает обмотка
возбуждения в поперечном сечении магнитопровода. Пренебрегая рассеиванием
магнитного потока вдоль магнитопровода и вокруг обмотки возбуждения считаем,
что магнитный поток, замыкающийся через поперечное сечение магнитопровода, полностью
пронизывает секции системы измерительных обмоток. Магнитный поток,
пронизывающий каждую секцию, индуцирует ЭДС
по закону электромагнитной индукции, которая записывается в виде:
(3.1)
Где 
- угловая частота питающего напряжения 
;
– число витков одной секции;
– магнитный поток, пронизывающий секции воздушного сечения.
Так как магнитопровод изготовлен из сплошной
конструкционной стали, то в его теле появляется сильно выраженный поверхностный
эффект. При этом магнитный поток по поперечному сечению распространяется не
равномерно, т.е. в центре сечения магнитный поток получает минимальное
значение, а вблизи его поверхности - максимальное. Как известно из литературных
источников, плотность магнитного потока близкого к поверхности магнитопровода
можно считать эквивалентным магнитному потоку создаваемого со стороны
постоянного тока. При таком обстоятельстве закон полного тока можно записать по
замкнутому контуру 
,
который записывается в виде:
(3.2)
Где 
- ток возбуждения протекающий через обмотки возбуждения;
– число витков обмотки возбуждения;
– величина воздушного зазора между магнитопроводом-1 и железного
листа;
– соответствующие участки длины
магнитосиловые линии;
– соответствующие напряженности
магнитного поля в принятой декартовой координатной системе.
Определяя напряженность магнитного
поля в средней части сечения, соответствующего длине 
находим функциональную связь между 
–
и 
в результате из (3.2) получим:
(3.3)
Зная напряженности 
магнитного поля, находим магнитный поток 
, пронизывающий обмотки
измерительной секции, который с учетом (3) записывается в виде:
(3.4)
Где 
– соответственно, относительная магнитная проницаемость материала
магнитопровода и магнитная постоянная.
Для дальнейшего исследования, ток возбуждения 
удобно выразить через напряжение
в комплексной форме,
Тогда формула магнитного потока записывается в виде:
(3.5)
где
– активное сопротивление обмотки
возбуждения;
– индуктивность обмотки возбуждения;
– напряжение питания.
Индуктивность 
находим через поток сцепления т.е.
(3.6)
Подставляя (3.4) в (3.7), после некоторых
преобразований и обозначений получим:
=
, (3.7)
Где 
– коэффициент, зависящий от геометрических размеров и параметров
материала.
Подставляя (3.5) в (3.6) и дальнейшем в (1) получим:
(3.8)
Здесь 
является ЭДС, полученной в одной измерительной секции. ЕДС 
в цепи измерительной секции создает ток, протекающий через
сопротивление 5. Так как величина этих сопротивлений весьма больше, чем
сопротивление самой секции, то ток индукции получается незначительным. При этом
ЭДС секции, определяющийся по формуле (3.9), для всех измерительных секций
остается неизменным, но оно переходит с одной секции в другую путем перемещения
магнитопровода в диапазоне измерения.
На основании проводимых исследований было установлено,
что выходное напряжение 
определяется в виде:
(3.9)
где n – число секций. При переходе
магнитного поля, полученного магнитопроводом от первой секции ко второй,
величина 
уменьшается на
, а во второй секции это напряжение
увеличивается на
. В результате при переходе
магнитопровода где n – число витков секций, при
перемещении магнитопровода от первой секции ко второй величина 
уменьшается на
; но во второй секции
напряжение 
увеличивается на
. В результате при переходе
магнитопровода ко второй секции, согласно формуле (3.9), изменение напряжения
увеличивается на 2
.
Если уменьшение принято со знаком минус,
а увеличение
с плюсом тогда суммарное напряжение будет
-
. Аналогичным образом получится
изменение напряжения при переходе магнитопровода от второй секции к третьей,
где получится -
. При дальнейшем перемещении
магнитопровода этот процесс повторяется.
Здесь изменение выходного напряжения прямо
пропорционально перемещению X подвижного магнитопровода, поэтому
выражение, указанное внутри квадратной скобки, в зависимости от X можно выразить в более простом
виде:
(3.10)
Где 
– коэффициент пропорциональности, зависящий от электромагнитных
параметров и геометрических размеров магнитопровода и обмотки секции.
Согласно формуле (38) коэффициент пропорциональности К записывается в виде:
(3.11)
На основании формулы (3.11), записанной для общего
случая, проведен расчет и построена характеристика рассмотренного датчика. Как
видно из (3.10) рабочая характеристика датчика является линейной в указанном
диапазоне X.
4.
Заключение. Предлагаемый датчик может работать только на
переменном напряжении питания. Для увеличения диапазона измерений достаточно
увеличить длину измерительного магнитопровода и соответственного числа секций.
При этом линейность рабочей характеристики остается прежней. Датчик может быть
применен в информационно-измерительных системах и в управлении технологическими
процессами в различных областях промышленности.
Литература
1.
Зарипов М.Ф.
Преобразователи с распределенными параметрами, М., Энергия, 1969, 176 с.
2.
Конюхов
Н.Е., Медников Ф.М., Нечаевский М.Л. Электромагнитные датчики механических
величин, М.: Машиностроение, 1987, 255 с.
3.
А.С. (СССР)
1647229. Трансформаторный преобразователь линейных перемещений. М., БИ №17,
15.05.91г.
4. Ф.И.Мамедов, Асадова
Р.Ш., К.Ф.Асадова. Индуктивный
преобразователь линейных и угловых перемещений. Патент Азербайджанской
Республики И
2008 0051, Баку, 07.04.2008
5. Ф.И.Мамедов, Асадова
Р.Ш., К.Ф.Асадова, С.Г.Асад-заде. Двухмерный индуктивный преобразователь для
измерения линейных и угловых перемещений, «Мехатроника, автоматизация,
управление», Изд-во «Новые технологии», 2011, № 8(125), с.14-16
F.I.
Mamedov, R.B. Dadasheva, R.A. Huseynov, R.Sh. Asadova, Sh.T. Mamedova, S.Q. Hidayatzada
Large linear displacement
sensors for information measurement control systems
Meeting the
reliability, quality and cost-effectiveness requirements of elements of control
systems requires new developments in the field of information measurement and
computing equipment. A special emphasis is placed on the development of
electromagnetic sensors of control systems. To measure large linear
displacement, the authors have designed a sensor, carried out calculations and
built the characteristic of the designed sensor. The sensor can be used in
information measurement systems and in the management of technological
processes in various industries.
Keywords: control
system, information measurement and computing equipment,
electromagnetic sensors, linear displacements