К.т.н. Твердоступ Н.И.

Днепропетровский национальный университет им. Олеся Гончара

АНАЛИЗ НИЗКОЧАСТОТНОГО ГИРАТОРА НА

КОНВЕРТОРАХ ОТРИЦАТЕЛЬНОГО СОПРОТИВЛЕНИЯ

В схеме гиратора, выполненного на конверторах отрицательного сопротивления, устойчивое инвертирование импеданса в общем возможно при тщательном согласовании параметров составляющих элементов, которое сводится к обязательному соблюдению взаимного равенства сопротивлений всех резисторов комбинированной обратной связи [1, 2].

Целью настоящей работы является уточнение конкретных условий согласования параметров элементов гиратора для обеспечения устойчивого инвертирования импеданса с заданным коэффициентом преобразования.

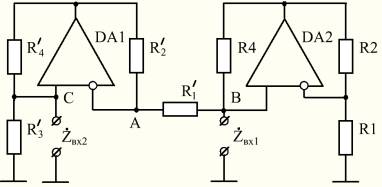
“Классический” гиратор на конверторах отрицательного сопротивления (рис.1) содержит два операционных усилителя DA1 и DA2 с элементами комбинированной обратной связи и а также резистор связи.

Рис. 1 – Гиратор на конверторах отрицательного сопротивления

Гиратор обладает свойством взаимности [1], поэтому произвольный импеданс нагрузки можно подключать к любой паре зажимов или . Рассмотрим, каким будет импеданс соответствующей пары зажимов при подключении нагрузки к противоположной паре.

При подключении к зажимам входные импедансы конверторов отрицательного сопротивления в точках А и В будут соответственно равны [3]

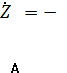
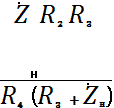, (1)

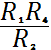(2)

а входное сопротивление со стороны зажимов

. (3)

Выражение (3) с учетом (1) и (2) можно представить, как

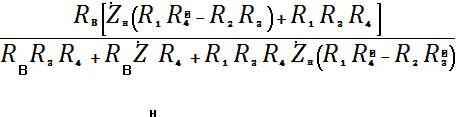. (4)

Выражение (4) при выполнении условия

(5)

и с учетом (2) преобразуется к виду

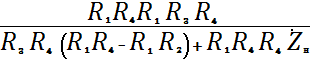. (6)

При выполнении следующего условия

(7)

выражение (6) принимает окончательный вид уравнения гиратора, изменяющего характер импеданса нагрузки

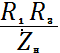. (8)

Действительно, если в качестве нагрузки используется, например, индуктивность , то из (8) следует

= ,

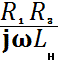отсюда , что указывает на емкостной характер импеданса на зажимах , обратный индуктивному характеру импеданса на зажимах .

Таким образом, одновременное выполнение условий (5) и (7) обеспечивает справедливость уравнения гиратора (8).

Рассмотрим входной импеданс гиратора на зажимах при подключении нагрузки к зажимам . В этом случае входной импеданс конвертора DA2 в точке В с учетом параллельно подключенной нагрузки равен [3]

=

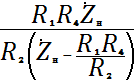
а в точке А соответственно

.

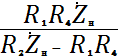Конвертор DA1 преобразует в импеданс, который в точке С имеет вид

.

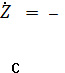
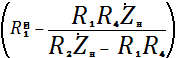Так как подключен параллельно , то входная проводимость гиратора имеет вид

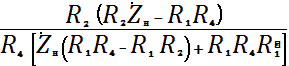= + . (9)

Из (9) следует, что при одновременном выполнении условий (5) и (7) входной импеданс гиратора со стороны зажимов равен

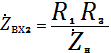. (10)

Выражение (10) полностью совпадает с (8). Это подтверждает симметричность гиратора на конверторах отрицательного сопротивления, возможность равноценного подключения нагрузки к любой паре зажимов.

Основным фактором эффективного инвертирования импеданса нагрузки, является выполнение условий (5) и (7), сводящееся к точности выбора сопротив-

лений указанных резисторов. При нарушении этих условий в гираторе возможно возникновение паразитных колебаний из-за самовозбуждения, ибо, как следует из (4), (6) и (9), в составе входного импеданса при этом одновременно появляются отрицательные активная, индуктивная и емкостная составляющие.

Физический смысл выражений (5), (7) можно уточнить, исключив сопротивление связи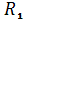. В этом случае получим соотношение

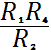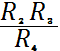= , (11)

показывающее, что суть согласования заключается в достижении равенства входных сопротивлений конверторов. Исходя из формы записи уравнений гиратора (8) и (10) условие согласования (11) целесообразно записать в виде

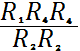= . (12)

В этом случае в (8) и (10) произведение сопротивлений является коэффициентом преобразования, величиной которого можно управлять всего лишь одним параметром - сопротивлением связи , не нарушая, при этом, условие согласования (12).

Вывод. Гиратор является согласованным при достижении равенства входных сопротивлений конверторов отрицательного сопротивления. Коэффициент преобразования гиратора определяется величиной сопротивлением связи.

Литература:

1. Титце У., Шенк К. Полупроводниковая схемотехника: в 2 т.: пер с нем. – Т.2. – М.: Додэка - ХХI, 2008. – 942 с.

2. Волович Г.И. Схемотехника аналоговых и аналого-цифровых электронных устройств. – М.: Додэка - ХХI, 2005. – 528 с.

3. Твердоступ Н.И. Обобщенная модель преобразователей импеданса // Вісник Дніпропетр. ун-ту. Фізика. Радіоелектроніка. – 2010. – Вип. 17, №2. – С. 103 - 108.