опыт линеаризации кинетических процессов
в полидисперсных системах
Стрельцова А.А.,
Гарькина И.А., Гарькин И.Н.
Пензенский государственный университет архитектуры и
строительства
Как правило,
кинетические процессы формирования физико-механических характеристик композитов
являются нелинейными. Приведение их к линейному виду существенно облегчает
аналитические исследования. Для этого использовались замены переменных:
![]() .
.
При выборе
между степенными и показательными функциями пользовались простыми графическими
правилами. По экспериментальным данным ![]() ,
, ![]() , определялись точки
, определялись точки ![]() ,
, ![]() и наносились на
график. Коэффициент
и наносились на
график. Коэффициент ![]() приближенной прямой
принимался за начальное приближение параметра
приближенной прямой
принимался за начальное приближение параметра ![]() показательной или
степенной функции. В случае планируемых измерений выбирались две последовательности точек:
показательной или
степенной функции. В случае планируемых измерений выбирались две последовательности точек: ![]() (арифметическая
прогрессия);
(арифметическая
прогрессия); ![]() (геометрическая
прогрессия). Определялись соответствующие выходные величины:
(геометрическая
прогрессия). Определялись соответствующие выходные величины: ![]() - в точке
- в точке ![]() ,
, ![]() - в точке
- в точке ![]() ,
, ![]() ; вычислялись отношения последовательных результатов
; вычислялись отношения последовательных результатов 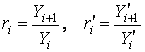 ,
, ![]() . При
. При ![]() выбиралась
показательная функция, и оценивался ее параметр:
выбиралась
показательная функция, и оценивался ее параметр:  ; при
; при ![]()
![]() выбиралась степенная
функция, а ее показатель оценивался в виде
выбиралась степенная
функция, а ее показатель оценивался в виде  .
.
Приведем основные замены переменных,
использовавшихся при линеаризации:
![]() – для показательной
функции
– для показательной
функции ![]() ,
,
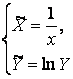 –
для показательной функции
–
для показательной функции ![]() ,
,
![]() – для дробно-линейной
– для дробно-линейной ![]() ,
,
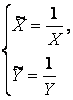 – для
дробно-линейной
– для
дробно-линейной 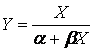 ,
,
![]() – для гиперболической
– для гиперболической ![]() ,
,
![]() – для логарифмической
– для логарифмической ![]() ,
,
![]() – для логарифмической
– для логарифмической ![]() ,
,
 – для степенной
– для степенной ![]() .
.
Степень
аппроксимирующего полинома определялась
с использованием разложения по ортогональным полиномам Чебышева ![]() . Исходили из
справедливости гипотез: значения
. Исходили из
справедливости гипотез: значения ![]() известны точно; значения
известны точно; значения ![]() содержат погрешности с
приближенно гауссовским распределением и дисперсиями, равными
содержат погрешности с
приближенно гауссовским распределением и дисперсиями, равными 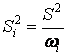 . По данным
. По данным ![]() последовательно
строились, используя МНК, приближения полиномами со степенями
последовательно
строились, используя МНК, приближения полиномами со степенями ![]() :
:
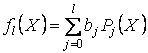 ,
, 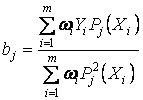 .
.
Максимальная степень полинома
определялась, исходя из конкретной задачи (в большинстве случаев - ![]() ). Тогда для остаточных сумм квадратов
). Тогда для остаточных сумм квадратов 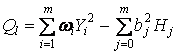 оценки дисперсии равны
оценки дисперсии равны ![]() (соответствуют
различным степеням
(соответствуют
различным степеням ![]() ). Степень полинома увеличивалась, пока оценки
). Степень полинома увеличивалась, пока оценки ![]() заметно убывали. Выбор
степени
заметно убывали. Выбор
степени ![]() полинома производился,
исходя из точности (по значению
полинома производился,
исходя из точности (по значению ![]() , при котором оценка
, при котором оценка ![]() минимальна -
минимальна - ![]() или по значению
или по значению ![]() , после которого оценка
, после которого оценка ![]() перестает заметно убывать
-
перестает заметно убывать
- ![]() ). Если при всех степенях
). Если при всех степенях ![]() выбранное условие не
достигалось, то принимали максимальную степень полинома
выбранное условие не
достигалось, то принимали максимальную степень полинома ![]() .
.
Для выбора степени
полинома использовались и методы перекрестного выбора. Все данные разбивались
на ![]() группы. Одна из групп
являлась проверочной, а по медианным точкам остальных групп строился полином
группы. Одна из групп
являлась проверочной, а по медианным точкам остальных групп строился полином ![]() . Согласие полинома с исходными данными оценивалось по его
отклонению от медианы проверочной выборки:
. Согласие полинома с исходными данными оценивалось по его
отклонению от медианы проверочной выборки: ![]() .
.
Описанная
процедура многократно повторялась, принимая последовательно каждую из групп за
проверочную. В итоге определялся суммарный показатель адекватности полинома ![]() исходным данным:
исходным данным: 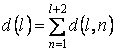 .
.
В качестве искомой степени полинома
принималось то значение ![]() , для которого показатель
, для которого показатель ![]() минимален.
минимален.
Указанные
способы использовались при идентификации процессов формирования отдельных свойств (частных критериев) композиционных материалов. В последующем
результаты использовались при определении аналитического выражения обобщенной целевой функции по выбранному
множеству частных критериев.
Литература
1.Гарькина
И.А., Данилов А.М. Опыт разработки композиционных материалов: некоторые аспекты
математического моделирования // Известия ВУЗов. Строительство. – 2013. – №8 (656). – С.28-33.