ФОРМАЛИЗОВАННЫЕ ОЦЕНКИ КАЧЕСТВА СИСТЕМ

Куликова А.С., Гарькин И.Н., Данилов А.М.

Пензенский государственный университет архитектуры и строительства

Определение и обеспечение гарантированного качества в рамках какой-либо теории возможны лишь приближенно, так как представления о формировании структуры и свойств системы всегда приближенные (всегда в описании системы что-то будет оставаться неучтенным; нельзя получить абсолютно точные результаты измерений и т.д.). Речь может идти лишь о том, чтобы значения показателей лежали в обоснованных допустимых пределах, чтобы полученный уровень гарантированности качества позволял оценить риск (количественно) от невыполнения заданных требований.

Эти проблемы в той или иной мере решаются с применением вероятностных методов (корреляционный анализ, экспертные оценки, ранговая корреляция и т.д.). На практике наибольшее распространение получили экспертные оценки. Эффективность использования методов экспертных оценок многократно подтверждалась при когнитивном моделировании сложных систем. Так, оценка качества материала осуществлялась по известным сведениям о его свойствах (единичных показателях), например, в факторном пространстве () определялся некоторый комплексный (обобщённый) показатель , учитывающий влияние принятых единичных показателей :

Y = f (y_1, y_2,..., y_m).

Наиболее простым путем формирования функционала является аппроксимация функции отклика некоторой приближающей функцией; в частности, представление комплексного показателя в виде линейной или квадратичной функции единичных или частных критериев (показателей). Коэффициенты этой функции будут весовыми коэффициентами соответствующих частных критериев. В случае линейной функции

.

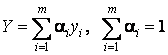При использовании итерационной процедуры поиска коэффициентов a_i она продолжается до выполнения условия

,

e – заданная малая величина. Результатом описанной итерационной процедуры является получение матрицы весовых коэффициентов

.

В частности, были определены весовые коэффициенты для оценки качества эпоксидного композита. Результаты приводятся в таблице 1.

Таблица 1.

Свойства	Эксперты					ai^(1)
	1	2	3	4	5
Плотность	0,2	0,3	0,1	0,3	0,1	0,2
Пористость	0,3	0,3	0,3	0,4	0,2	0,3
Прочность	0,5	0,4	0,6	0,3	0,7	0,5

На первой итерации «степень доверия» ко всем экспертам принималась одинаковой (k_j⁽⁰⁾ = 1).

На второй итерации весовые коэффициенты определялись с учётом разнородности экспертов и их различной компетентности (коэффициенты k_j⁽¹⁾ отличаются друг от друга). Поэтому на второй итерации весовые коэффициенты определялись в виде:

.

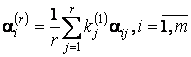Для вычисления коэффициентов k_j⁽¹⁾ вводилась мера

.

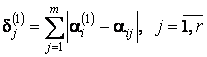Принималось:

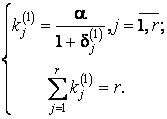
При указанных условиях

с учетом

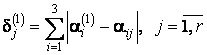
получили d₁⁽¹⁾ = 0; d₂⁽¹⁾ = 0,2; d₃⁽¹⁾ = 0,2; d₄⁽¹⁾ = 0,4; d₅⁽¹⁾ = 0,4.

По значениям

,

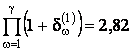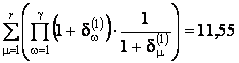
были определены коэффициенты

; ; ; .

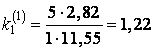Далее определялись весовые коэффициенты :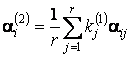

a₁⁽²⁾ = 0,2; a₂⁽²⁾ = 0,3; a₃⁽²⁾ = 0,5.

Комплексный показатель является линейной функцией единичных (частных) показателей (критериев):

Y = 0,2 y₁ + 0,3 y₂ + 0,5 y₃.

Как видим, наиболее значимым показателем является прочность.

Литература

1.Данилов А.М., Гарькина И.А. Сложные системы: идентификация, синтез, управление. – Пенза:ПГУАС.- 2011. – 308 с.