Технические науки / 6.Электротехника и радиоэлектроника.

Шумай Т.А., к.т.н. Черных А.Г.

Иркутский государственный аграрный университет, Россия

ДВОЙСТВЕННЫЙ ХАРАКТЕР УРАВНЕНИЙ ЛАГРАНЖА-МАКСВЕЛЛА ПРBМЕНИТЕЛЬНО К ВРАЩАЮЩИМСЯ ЭЛЕКТРОМЕХАНИЧЕСКИМ ПРЕОБРАЗОВАТЕЛЯМ

Вращающиеся электрические машины (ЭМ) относятся к классу электромеханических преобразователей (ЭМП), т.е. устройств, реализующих одно физическое явление – взаимное преобразования электрической, магнитной и механической энергии. В общем случае изучение ЭМП распадается на три задачи:

1. физическое описание преобразователя;

2. математическое описание – составление уравнений движения системы;

3. исследование уравнений движения машины с учетом конкретных условий ее работы.

Как правило, рассмотрение любого ЭМП начинается с выбора законов, которые соответствуют физическим процессам в преобразователе и математического аппарата, с помощью которого данные процессы описываются.

Учитывая, что вращающаяся ЭМ состоит из ряда взаимодействующих электромагнитных контуров, часть которых неподвижна, а часть вращается, то физика процессов происходящих в таких устройствах тесно связана с двумя законами электромагнетизма: законом Фарадея и законом Ампера.

Получить математическое описание ЭМП можно различными способами с точки зрения формальности применяемой техники анализа. В данном контексте среди способов получения уравнений ЭМП можно выделить два основных.

Первый способ получения уравнений ЭМ основан на использовании физических законов. При таком подходе к составлению уравнений движения системы необходимо учитывать, что применение физических законов мало формально и требует большой профессиональной интуиции, особенно, когда ЭМП имеет нетрадиционную конструкцию, например, ЭМ со сверхпроводящими обмотками возбуждения [1]. Уравнения движения получают из законов физики и электротехники: Фарадея, Ампера, Кирхгофа и др. Для определения механических сил взаимодействия между проводящими частями ЭМ используется закон сохранения энергии и принцип возможных перемещений.

Второй способ вывода уравнений электромеханического равновесия ЭМ основан на вариационных принципах и в большей степени формализован. В основе этого принципа лежит подход, при котором электромагнитные процессы в ЭМП представляются в форме уравнений Максвелла, подобных уравнениям Лагранжа для механических систем, а затем, с учетом сил электромеханической связи между подвижными и неподвижными частями ЭМ, полученные уравнения для электромагнитных цепей и механических конструкций объединяются в единую форму дифференциальных уравнений Лагранжа-Максвелла для электромеханических систем [2].

Функция Лагранжа при этом заменяется на функцию Максвелла для энергии электромагнитного поля и в уравнение вводятся обобщенные электрические координаты (заряды), а также их обобщенные электрические скорости (токи). При этом каждая электрическая координата, выбранная в соответствии с правилами топологии для электрических цепей, измеряет общее количество заряда, который переносится через данную точку в каждой ветви расчетной схемы замещения ЭМ от начального момента времени t₀ до произвольного момента t.

Совокупность электрических n и механических m (по числу степеней свободы) образует некоторую систему координат пространства. С точки зрения динамики вращающейся ЭМ, такая система координат является квазиголономной динамической системой. Это связано с рядом условий, налагаемых на характер преобразования электрических и механических координат, что, в конечном счете, позволяет упростить конечную форму единых уравнений.

При этом структура результирующего (n + m)- мерного пространства ЭМ зависит от режима ее работы: для вращения с постоянной скоростью – обычное, евклидово; для режима ускорения – риманово, обладающее кривизной; для режима малых колебаний (качаний) – нериманово, обладающее не только кривизной, но и кручением. Необходимо отметить, что в любом отмеченном выше пространстве структуры электрические координаты (заряды) отсутствуют во всех измеряемых компонентах (электрических величинах), определяющих поведение ЭМ, а, следовательно, удовлетворяют цилиндрическому условию.

Таким образом, для (n + m)- мерного пространства с n- электрическими и m- механическими координатами имеется цилиндрическое условие, связанное с n-электрическими координатами. В результате все преобразования координат для таких динамических систем, как вращающиеся ЭМ ограничены данным условием, а потому голономны для угла поворота ротора θ не голономны для дифференциалов электрических координат (токов), хотя последние зависят только от угла θ. Как следствие, в новой системе координат компоненты ЭМ, входящие в уравнения электромеханического равновесия в неголономной системе отсчета зависят только от координаты старой системы (угла θ), которая преобразуется голономно. Данное обстоятельство позволяет рассматривать преобразования самих равновесных уравнений ЭМ, определенных в неголономной системе отсчета, как голономные. В конечном итоге, это дает возможность получать преобразованные уравнения ЭМ после введения дополнительных связей, обусловленных соединением элементов (обмоток) машины друг с другом или с внешними цепями.

Большинство ЭМ имеют одну степень свободы, т.е. одну механическую координату – угол θ. Число электрических координат ЭМ, определяется числом входящих в ее конструкцию электромагнитных контуров. При этом в соответствии с принципом дуальности, для получения уравнений электромеханического равновесия ЭМ принято рассматривать две группы электрических переменных, аналогичных переменным, характеризующим механические системы (табл. 1).

Таблица 1 – Аналоги механических и электрических переменных в электромеханических системах

Механическая система	Электрический аналог (I-ая группа)	Электрический аналог (II-ая группа)
Обобщенная координата – θ Обобщенная скорость – Обобщенная сила – Обобщенный импульс –	Потокосцепление – Ψ Напряжение – Ток – Заряд –	Заряд – Ток – Напряжение – Потокосцепление – Ψ

Принимая во внимание данные табл. 1 определим кинетическую (Т) и потенциальную (V) энергии ЭМ с двумя обобщенными координатами: углом поворота ротора θ и потокосцеплением Ψ. Имеем

где р – обобщенный импульс, q – обобщенная координата, – обобщенная скорость, f – обобщенная сила, W_e – запасенная энергия в электрическом поле, W_m – запасенная энергия в магнитном поле.

Аналогичным образом по данным табл. 1 определим энергии T и V для второй группы электрических переменных. Получим

Учитывая, что современные магнитные материалы допускают плотность запасенной энергии во много раз большую, чем существующие электропроводящие материалы, то ЭМ преимущественно являются магнитными устройствами (с магнитным полем связи). Как следствие, для ЭМ традиционной конструкции справедливо соотношение W_e << W_m.

Анализируя полученные выше соотношения можно сделать вывод о том, что первая группа электрических переменных дает в качестве кинетической энергии T_эл электрическую энергию W_e, а в качестве потенциальной энергии V_эл магнитную W_m. Таким образом, для первой группы аналогий магнитное поле потенциально и в соответствии с табл. 1 электрические токи аналогичны обобщенным силам, а напряжения – обобщенным скоростям.

Вторая группа электрических переменных дает в качестве кинетической энергии T_эл магнитную энергию W_m, а в качестве потенциальной энергии V_эл электрическую энергию W_e. В этом случае электрическое поле потенциально, напряжения аналогичны обобщенным силам, а токи – обобщенным скоростям.

Полная запасенная энергия электромагнитного поля W_em является непрерывной функцией мгновенной конфигурации (взаимного расположения электромагнитных контуров) ЭМ, определяемой значением механической координаты (углом θ), а изменение запасенной электромагнитной энергии приводит к возникновению обобщенных сил электромеханической связи F_em. При этом силы F_em являются непрерывными функциями угла θ и электрических независимых переменных: потокосцеплений и напряжений – для первой группы; зарядов и токов – для второй группы [3]. Причем все эти функции непрерывны и взаимно однозначны, электрические потери в электромагнитных контурах ЭМ рассматриваются отдельно, а их параметры рассчитываются для двумерной расчетной модели конкретной машины в предположении, что обмотки статора и ротора симметричны, токи статора и ротора рассматриваются как поверхностные токовые слои; линейные плотности тока в этих слоях предполагаются кусочно-непрерывными функциями соответствующих координат, в магнитной цепи машины отсутствует насыщение [1].

Если учитывать между витковые емкости в электромагнитных контурах ЭМ, то соответствующая любому контуру схема замещения может быть представлена в виде последовательной (R, L, C) цепочки. Уравнение электрического равновесия по второму закону Кирхгофа такой цепочки и соответствующие данному уравнению преобразования имеют вид

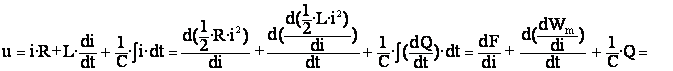
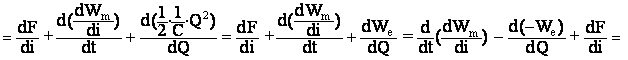
(1)

где – функция диссиципации (рассеяния), L= (W_m – W_e) – функция Лагранжа (силовая функция).

Уравнение (1) может быть преобразовано к виду

(2)

где – виртуальная работа сторонних (напряжения u) и диссипативных сил.

Виртуальная работа – это работа сил, совершенная по виртуальным перемещениям, которыми являются обобщенные координаты q. Если перемещения виртуальные совпадают с истинными, то справедливо равенство

(3)

Например, в уравнении (2) слагаемое может рассматриваться как электрическая система с рассеивающим элементом R и сторонней силой u.

Если принять в качестве электрических переменных вторую группу (табл. 1), то виртуальная работа для такой системы в соответствии с (3) определится выражением

где – обобщенная сила источника с напряжением u, – обобщенная сила рассеивающего элемента с сопротивление R.

Окончательно, учитывая уравнение Лагранжа второго рода, описывающее в области одной независимой обобщенной координаты (угла θ) уравнение движения ЭМ в виде дифференциального уравнения второго порядка относительно компонент вектора обобщенной координаты q и обобщенной скорости [3] и присоединяя к нему уравнения вида (3), векторная запись которого тождественна векторному уравнению Максвелла совпадающего по форме с соответствующим векторным уравнением Лагранжа с точностью до введенных электромеханических аналогий (табл. 1), получим систему векторных уравнений Лагранжа-Максвелла для ЭМ (в переменных θ, , и )

где – непотенциальные силы.

Роль потенциальной энергии здесь выполняет электрическая энергия, запасаемая в между витковой емкости обмоток, магнитная энергия аналогична кинетической энергии вращающегося ротора машины, падения напряжения на активных сопротивлениях обмоток аналогичны диссипативным силам (силам трения) ротора, а углу поворота ротора и угловой скорости вращения ротора здесь соответствуют независимые заряды и токи в электромагнитных контурах ЭМ.

Литература:

1. Коськин Ю.П. Синхронные машины с немагнитным ротором. / Ю.П. Коськин, Л.А. Цейтлин – Л.: Энергоатомиздат, Ленингр. отд-ние, 1990. – 280 с.

2. Лурье А.И. Аналитическая механика / А.И. Лурье. – М.: Физматгиз, 1961. – 824 с.

3. Уайт Д. Электромеханическое преобразование энергии: пер. с англ. / Д. Уайт, Г. Вудсон; под ред. С.В. Страхова. – М. – Л.: Энергия, 1964. – 528 с.