Технические науки/ Авиация и космонавтика
Dr Nickolay Zosimovych
Shantou University, Shantou, China
GENERAL TECHNIQUE for SOLVING
STRUCTURAL and PARAMETRIC OPTIMIZATION of FLYING VEHICLE
STRUCTURES
Keywords: Parametric optimization (PO), technical system (TS), flying vehicle (FV), design
and development (D&D), structural
optimization (SO), mathematical model (MM), standard
theoretical solutions (STS), engineering design
solutions (EDS), elementary
design base (EDB), airframe, prescribed form method (PFM), structure and parameter optimization (SPO), essential
features (EF), matrix, finite difference method (FDM), stress-strain
behavior (SSB), prescribed form method (DSM).
I. Introduction. The parametric
optimization (PO) methods enabling us to determine the optimal values of the
technical system (TS) parameters for a specified structure have been well
developed to date and successfully applied.
Besides optimization of parameters of the designed unit, considerable
attention of scientists and practical specialists is attracted to the problem
of decomposition of its structure [1-4]. This problem is very important and
fundamental, as it is virtually impossible to develop a unit with an
ill-conceived and ill-founded structure to a rational design level [5-7]. In its
turn, the flying vehicle (FV) structure influences the efficiency of TS [8]. In
order to improve technical and economic parameters of the designed product,
design and development (D&D) shall be conducted in three stages [4, 9-11].
Specific types of problems shall be solved at each stage.
II. Content of the Problem. Since the structural design process cannot be
completely formalized, the dialogue "designer - computer" is an
essential component of the process. Organization of the dialogue is one of the
central problems of the new aircraft structural design technology based on the
use of human-computer methods of parametric methods of structural and
parametric analysis and synthesis [2, 6]. The
main problem in the design dialogue when we choose a rational structure for
flight vehicle airframes is associated with a very large dimension of the
problem, describing the functioning of the designed unit. Calculations of
strength and aeroelastic stability of flight vehicle structures require a large
amount of computer resources. If we select a rational flight vehicle structure,
taking into account the impact of spectrum load, it becomes clear that
even advanced computers are not able to
solve the problem of organization of the "designer - computer"
dialogue by the application software, based on the reference methods of
structural analysis. At the same time, the use of quick-response, but
simplified models and methods for engaging in a dialogue with the computer may
be unacceptable as far as mismatch between needed calculation accuracy and the
roughness of simplified models and methods.
The suggested approach to the structural synthesis of FV structures
included into the airframe of FV provides a way to resolve this contradiction
by splitting the problem into two stages [2]:
1.
Obtaining standard theoretical
solutions (STS) by methods of mathematical programming of airframe units, which
implement the optimum distribution laws in terms of minimum mass and the efficiency of the units individually, and the airframe in
general within the specified load spectrum.
2.
Analysis and synthesis of structure
units with the use of interactive procedures in order to identify alternative
EDS for the units with their standard solutions, allowing to numerically assess
the error in the mass and rigidness distribution laws between EDS and STS and
to conduct a directed search of rational structure of FV structures included
into the airframe of the flight vehicle.
The current study of stress-strain condition of complex structures, as
well as rapid development of computer technologies and mathematical
optimization techniques create background enabling to solve the first-stage
problem of regarding a complex LV design as a single system with the necessary
detail, taking into account the whole complex of the basic requirements to it [12-19].
As for the second stage, it is necessary to study methodological and
mathematical aspects of EDS and STS identification to implement the
"designer - computer" dialogue, and to develop on this basis special
mathematical and application software.
Identification of the material objects, regardless of the subject area
and practical activities (engineering, biology, forensics, etc.) is subject the
same logical framework [20]. It involves finding such a set of deterministic
parameters of the studied objects, which allow you to evaluate the objects from
the position of their integral
characteristics and properties, which set, in its turn, clearly defines an
objects in a specified class [1, 11].
In
other words, when identifying objects and not being able to explore their
functional properties directly in their natural environment, you shall forecast
these properties based on the set of the most important parameters of these
objects [4, 16-19, 21-23]. Naturally, the validity of the identification
procedure will be determined by a set of parameters and relations between them.
Mathematically,
the identification problem refers to the inverse problems of mathematical physics
[1]. As a rule, these problems are ill-posed, since there may fail object that
fully implements the required operation laws, as not all sets of parameters can
be practically implemented. In this case, the identification will mean finding
of practically implementable object with a set of parameters, which shall
maximally correspond to predetermined functional properties.
When
solving inverse problems we have to answer the following three questions:
1.
Is there any solution for the problem
that has been set?
2.
If there is one, then is it the only
one?
3.
Is the solution stable, i.е. do any slight changes in source data result in slight changes in the
solutions?
If
the answer to the above questions is ‘yes’, the problem is well-posed.
Otherwise, the problem is ill-posed [24, 25].
In
the second stage of structural synthesis [2, 11], besides being well-posed the
identification procedure requires high efficiency of computer operations,
because the "speed" of the procedure preconditions not only the
efficiency of this approach to the choice of a practical unit design, but in
principle the possibility of interactive designer work with a computer.
In this definition of the structural and parametric problem of
optimization we assume that the external geometry of FV airframe, the
structural material and the load range have been determined in advance on the
previous stages of FV design.
III. Decomposition of Flight Vehicle Structures. The decisions taken in the early
stages of FV design not merely predetermine a set of decisions to be taken at
later stages but to some extent they are determined by these decisions themselves
[26-28]. Consequently, the choice of rational structures must be based on both
multivariate analysis and on the way to ensure materialization of this
structure. In order the FV structures could be materialized as a specific EDS,
it is necessary to select the unit structures based on the preformed SMs. These
are the assembly units obtained with consideration of technical and operational
requirements for specified levels of structures, as well as standards and
ranges of their construction elements existing in the industry. The structural
modules may in their turn consist of simpler SM [1, 11].
All the SM must be developed in advance for the specified class of FV and constantly complemented with new patentable design solutions. SM set represent an elementary design base (EDB). Another feature conditioned by hierarchical D&D tasks is a strong information connectivity of design stages, based on the coordination of the input and output information between the individual stages. This feature does not allow completing design in one cycle, and makes it necessary to create an iterative process between the design stages, taking into account the structure general for all decomposition stages [29]. For example, the choice of construction material for FV structures cannot be the responsibility of one D&D stage. Since its characteristics affect the following parameters:
· efficiency of FV as TS engaged in
fulfillment of specific monitoring tasks;
· technical and design excellence of the
FV for dynamic natural resource and environmental monitoring.
Hence, the structural features, including
structural material should be selected based on the analysis of the functional
properties and workability of the FV design [27]. This is possible only if we
organize an iterative process of FV design.
Organization of external iterative cycles at
the following stages:
· general design;
· structural design;
· design engineering
is
particularly ineffective. It is necessary to organize internal cycles between
adjacent stages in addition to the external ones. The purpose is to reduce the
dimension of the problem and to ensure the convergence of the external
iteration cycle.
In
order to provide convergence of internal cycles of structure design process it is
necessary to ensure the hierarchical consistency (intersection) of the levels within
the considered decomposition scheme [2, 3]. To do it, it is advisable to use the
procedure of structure and parameter
optimization (SPO) accepted in the design theory for complex technical systems,
which is to be used to estimate design versions based on the properties, which provide
the object with the optimum combination
of the parameters in the compared structures. We shall use the following method
for the structure localization at the levels of the decomposition scheme. We shall
present EDS structure at each level of the complex of the essential features in
two adjacent levels [1]: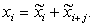 
In this case 
are the structural features, and
are parameters of the
structure of 
- level of decomposition. So,
selection of a rational EDS for FV structures represents a multilevel SPO [27].
There are proven in practice
guidelines for the construction of Decomposition schemes of multilevel structural
optimization (SO) [5], which
shall be used by us. They are as follows:
1. A multilevel SO problem shall be divided into several
two-level SO problems.
2. The structural variables shall be set in such a way that
it is possible to describe the variety of potential structures with their help.
These structures may be set either by expert suppliers, or implemented by mathware
and software.
3. A check for limitations (deliberately splitting impossible
structures off) should be introduced gradually in the process of structure
formation, and not afterwards.
4. The whole complex of limitations must represent a
hierarchically adjusted system according to the levels of design development [5,
30].
The multilevel SPO built on these principles (Fig.
1) is in line with decomposition of load-bearing structures (see Fig. 2.1) [27,
31].
Fig. 1. Multilevel SPO Diagram for FV
A multilevel decomposition scheme is
needed to reduce the dimension of the design problem. It reflects a particular
level of detailed elaboration of design solutions [4, 30]. Each level is a
functionally complete subproblem with a specific "physical" content. In the sequential decomposition scheme, the
information obtained after solving one of the sub-problems shall be initial for
solving the following one. As a result, the sub-problems are well ordered,
forming a "chain" of sub-problems. The sub-problems at each level
shall be decomposed in their turn into related sub-problems, typical for each
decomposition level. They are as follows:
·
set
generation;
·
set
contraction;
·
synthesis
of the structural features of the corresponding level [2].
If in order to solve the first two types of sub
–problems we use structural features of the same level, then in synthesis there
occurs mutual agreement (coordination) of structural features of the adjacent
decomposition levels. The design technology, based on the gradual rejection of
versions requires a large set of alternatives. There is no need to generate EDS
with full detailed elaboration of the structure of all possible versions, as
the structure of the object confines to a set of parameters essential for a
specified level at the various stages of the design process. The problem of
dimension and non-formalizability of all the factors influencing the choice of
the EF results in incapability to solve sub-problems at the level by methods of
mathematical programming in building a global optimization. For the organization
of decision-making under these conditions, you will require a system of
simulation models and interactive procedures of interaction with them [32-34].
In doing that you should consider both mathematical peculiarities of
sub-problems and their engineering content.
Let’s consider allocation of sub-problems for
different levels of the decomposition scheme similar in "physical"
content [27, 35].
Generation of EDS versions is decomposed by
structural features, like the two following procedures: contraction of EDS set
and selection of a rational TDS. The procedures of generating a set of
structural features 
at all hierarchical levels
are of linked together. The EF set contraction procedures involve parametric
optimization and subsequent rejection of the EF vectors during the analysis of
the effectiveness with application of simulation systems. The synthesis of EF at
each level ends up with a selection of the EF vector for the specified level (
) as a
result of structural and parametric optimization. However, as it has been
stated above, EF of the following level serve as variable parameters, which
optimal combination lets estimate and select EF of the referred level. By selecting vector (
) we
determine the subset corresponding to it 
[1, 2].
Set contraction and synthesis of the EF are implemented
by simulation system (SS) with a specified "physical" content [27]. SS
refer to a set of simulation models and interactive procedures of communication
with these models. Simulation systems are problem-focused on their levels of
detail EDS elaboration. They simulate operation of the FV as a technical
system, performance of the airframe, performance of the FV structures, and performance
of the structural modules.
The decision-making procedures with application
of simulation systems require, as a rule, the development of new methods for
solving very diverse extremal problems. There exists a large number of research
programs designed for aircraft engineering analysis. But it is very difficult
to apply them for simulation models. The fact that they are not cost-effective,
poorly adapted to multiple iterative calculation, hardly interface with other
programs, and do not have a unified database. Besides computation procedures (simulation
system base), application software must contain formalized part of the
interactive procedures that allow the designer to conduct a dialogue with the
simulation system.
The content of the dialogue in the phase of FV
structures design involves economical
method to find the best constructive and technological solutions with the help
of application software specially developed for this purpose, but not due to roughening
of computational models and unjustified disregard of the complexity of FV operation
in general [31-34]. Under these conditions, the dialog with simulation models
should be built on a mathematical basis, different from that applied for the
solution of direct problems. The author believes that the ill-posed problem theory
[24, 36] combined with the apparatus of linear algebra may be a promising
concept in the organization of the interactive procedures.
We can naturally suppose that that a specific problem orientation of FV CAD may go some way
to modify the decomposition scheme in the number of levels and the number
of sub-problems. In any case,
the implementation of the proposed
concept requires a high level of
technical equipment, basic software and information support and special application software [2]. This is an expensive resource
provision of technical progress, without
which we cannot hope for success
in the field of automation of
D&D in the aircraft industry [11].
IV. Modelling Solutions for Flight
Vehicle Structures. Obtaining
of STS for FV structures of FV can be fully formalized with mathematical programming
techniques, a system of mathematical models describing the physical status of
the construction and operating restrictions. The restrictions are divided into
two groups. The first one includes operational restrictions traditional for FV
structures (strength, stability). The second group includes restrictions for FV
frame structure (natural frequency, aeroelastic stability of FV). The
optimality criterion is a criterion of a minimum weight of the FV. In
accordance with the hierarchy of operating restrictions, we propose to use
models of two levels for finding the optimal distribution of material between
integral units of airframe:
· MM of FV which body is schematized
with a beam and the bearing surfaces with plates;
· mathematical models of units –
anisotropic shells and plates
To construct mathematical models of the units
we used the finite difference method (FDM), which main advantage is in the
invariance of the simulation model with respect to EDS of the units [37].
Under the influence of power and heat, the stress-strain
behavior (SSB) of an anisotropic shell or of a plate with variable thickness shall
be described by the system of equations (strain equilibrium and compatibility)
[38] concerning the force functions 
and deflections 
recorded
in finite differences for 
centers in the net domain,
approximating unit construction [39]:
(1)
where 
is a coefficient
matrix; 
are the
vectors of the unknown and right-hand sides of the equations describing SSB of 
- unit (
),
is
the number of units included into the airframe of the FV. The determined
deflections 
let
us determine equivalent stress 
in
the net domain centers and they shall be compared to the assumed 
. The unit constructions shall meet the
requirement of static strength [1], if the following conditions are met
In order to solve the problem of FV airframe
unit’s stability we shall use a dynamic method (method of small oscillations) [40].
This method is well combined with FDM and can solve the static and dynamic
stability problem. The equations for small oscillations of the structure units shall
be derived from the corresponding equilibrium equations by replacing static
deflections and loads with dynamic ones:
(2)
where is rigidity
matrix; 
are complex
frequencies and structural modes of 
- unit;
is a unity
matrix.
From the vanishing of the characteristic
determinant of the system of equations (2) we shall determine the values of
complex vibration frequencies. The status of the structure [1] shall be
determined according to the sign of real parts 
: stable
or not
and the
value of the imaginary part of the complex frequency 
determines
the character of this status: static 
or dynamic 
Under the influence of
aerodynamic forces, the bearing surfaces may have both static form of loss of
stability (divergence) and dynamic one (flutter). Loss of stability in body
sections of unmanned FV shall be static under the influence of compressive
forces.
To construct a mathematical model of FV we
shall use a prescribed form method (PFM). The prescribed forms are natural
oscillations of the structure in vacuum. The main advantage of PFM is in its operational
economy. The system of differential equations describing oscillations of the FV
in the aerodynamic flow and compiled according to PFM is as follows:
(3)
where 
are matrices
of mass rigidity of FV; 
are matrices
of aerodynamic forces and aerodynamic damping; 
is a
vector of generalized coordinates; 
is a
speed of aerodynamic flow.
Simultaneous equations order (3) is determined
by a number of considered forms of natural oscillations of the structure 
[1].
The stability of FV airframe requires that the
real parts of complex oscillation frequency spectrum 
obtained by solving the
eigenvalue problem for the system (3) [12] were negative 
In some cases due to requirements to ensure
stability of the "aeroelastic FV - control system" circuit cycle there
may be additionally imposed restrictions on the frequency of natural
oscillations of FV:
The problem of finding optimal material
distribution 
among 
units
of FV airframe is a mathematical programming problem, which is to be solved by
the random search method, and resolves itself as follows. Using
set 
corresponding to static
elastic equilibrium of the units [39]:
;
and in dynamics [3]:
;
and aeroelastic equilibrium of FV:
which meets strength conditions:
and unit
stability conditions:
, 
as well as restrictions on the frequency of
natural oscillations:
and the requirement of aeroelastic equilibrium
of FV airframe:
find vector 
for
which weight of FV
(here 
are mass density and
effective thickness of construction material in the component 
of the unit
) takes the
minimum value. When a spectrum of loads is set, all the conditions applied for
vector 
must be met
for each loading mode [1].
Conclusion.
1.
We
have developed the methods of structural and parameter optimization for FV
structures, formulated three types of problems for structural and parametric
decomposition of FV structures and general principles of decomposition of
design objects.
2.
We
have performed structure decomposition for the specified technical system
structure, synthesis of FV structures and suggested a general scheme for
solving the problem.
3.
In
the process of identification of material objects for structural and parameter
optimization we have formulated and analyzed the content of the structural and
parameter optimization problem for FV structures included into their airframes.
4.
In order to obtain standard solutions, we have done formalization of FV
structures using mathematical programming methods, a mathematical model system
based on the defined-shape and finite difference method describing the physical
condition of the structure and operating limitations.
References
1. Голубев И.С., Андреев В.В., Парафесь С.Г. Методы
структурно-параметрической оптимизации силовых авиационных конструкций: Учеб.
пособие. – М.: Изд-во МАИ, 1991. – 68 с.
2. Зосимович
Н.В. Декомпозиция задач синтеза структуры силовых конструкций ДПЛА для
оперативного природоресурсного и экологического мониторинга окружающей среды // Cборник научных трудов по материалам
научно-практической конференции «Научные исследования и их практическое
применение. Современное состояние и пути развития», 1-15 октября
3. Первозванский А.А., Гайцгори В.Г. Декомпозиция,
агрегирование и приближенная оптимизация. М.: Наука, 1979.
4. Лось Л.В. Теория структуры
конструкций технологичных машин и приборов. – Житомир:. Житом. сельскохоз. ин-т,
1991. – 167 с.: ил.
5. Бирюк
В.И., Липин Е.К., Фролов В.М. Методы проектирования рациональных конструкций ЛА // Труды ЦАГИ, № 1776, 1976.
6. Ланцош
К. Практические методы прикладного анализа. М.: Физматгиз, 1961.
7. Валуев
М.И., Харченко В.П., Яппаров А.Н. Системотехніка та основи проектування
аеронавігаційних систем: Навч. Посіб. – К.: НАУ, 2003. – 120 с.
8. Беспилотники / Аэрокосмический вестник. – 2005. - № 8. – К.: ООО «СПЕЙС-ИНФОРМ», с. 32-33.
9. Половинкин А.И., Бобков Н.К., Бум Г.Я.
Автоматизация поискового конструирования. – М.: Радио и связь, 1981.
10. Половинкин
А.И. Автоматизированные системы поискового конструирования // Материалы І Всесоюзного совещания по автоматизации
проектирования в машиностроении. АН БССР, Минск, 1978.
11.
Nickolay Zosimovych. Structural and Parametric Optimization for
Flight Vehicle Structures. “Areas of Scientific Thought - 2016/2017”, XII
International Scientific and Practical Conference, December, 30, 2016 –
January, 7, 2017, Technical Science, Vol. 8. Sheffield, UK: Science and
Education LTD. – PP. 59-68.
12. Научные
основы прогрессивной технологии / Г.И.
Марчук, А.Ю. Ишлинский, П.Н. Федосеев и др. – М.: Машиностроение, 1982.
13.
Канфилд Р.А., Гранул Р.В., Вонсайн В.Б.
Оптимальное проектирование конструкций при большом количестве ограничений // Аэрокосмическая техника. 1988.- № 10.- C. 78-88.
14.
Василенко М.В.,
Алексейчук О.М. Теорія коливань і стійкості руху: Підручник. – К.: Вища школа,
2004. – 525 с.
15.
Тимошенко С.П., Янг Д.Х., Уивер У. Колебания в
инженерном деле./ Пер. с англ. Л.Г. Корнейчука. – М.: Машиностроение, 1985. –
472 с.
16. Страуструп
Б. Язык программирования С++, спец. изд. / Пер. с
англ. – М.; СПб.: «Издательство БИНОМ» - «Невский Диалект», 2002. – 1099
с.
17.
Бондаренко Г.О. Синтез нейрон-нечітких
мереж // Матеріали ІІІ Міжнародної науково-прикладної конференції “Динаміка
наукових досліджень ‘2004”. Том 64. Технічні науки. – Дніпропетровськ: Наука
і освіта, 2004. с.17-18.
18.
Литвиненко Є.М. Ресурсне
планування в управлінні проектами // Матеріали ІІІ Міжнародної
науково-прикладної конференції “Динаміка наукових досліджень ‘2004”. Том 64. Технічні науки. – Дніпропетровськ:
Наука і освіта, 2004.- C.41-42.
19.
Чумаченко И.В., Кучмиев В.Г., Бугас Д.Н. Алгоритмические и инструментальные
средства автоматизированных систем обработки информации // Матеріали ІІІ Міжнародної науково-прикладної
конференції “Динаміка наукових досліджень ‘2004”.- Том 64. Технічні науки. – Дніпропетровськ: Наука і
освіта, 2004.- C.52-53.
20. Шлеер
С., Меллор С. Объектно-ориентированный анализ: моделирование мира в состояниях / Пер. с англ. – К.: Диалектика, 1993. – 240
с.
21.
Зосимович
Н.В. Использование сельскохозяйственной авиации в Украине для решения задач
экологического мониторинга и рационального использования природных ресурсов //
Авиация общего назначения - 2004. - № 4.
- C. 12-16. Харьков:
АОН.
22.
Зосимович Н.В. Определение
характеристик и разработка математической модели параметров транспортных
возмущений КА экологического мониторинга Земли // Матеріали І Міжнародної
науково-практичної конференції “Науковий потенціал світу
23.
Сарымсаков Х.Г. Оптимальные варианторазмеры сельскохозяйственных
самолетов // Вопросы проектирования и
расчета самолетов. Сборник научных трудов ТашПИ. – Вып.205, 1977. - C.18-23.
24. Тихонов
А.Н., Арсенин В.Я. Методы решения некорректных задач. – М.: Наука, 1986.
25.
Черноруцкий
И.Г. Методы оптимизации и принятия решений. СПб.: Лань, 2001.
26.
Зосимович Н.В.
Структурно-параметрическая оптимизация силовых конструкций дистанционно-пилотируемых
летательных аппаратов оперативного природоресурсного и экологического
мониторинга окружающей среды //
Региональный вестник молодых ученых. М.: Academa, 2005.- №3.- C. 97-98.
27. Зосимович Н.В. Методика решения декомпозиционных
задач синтеза структуры силовых конструкций ДПЛА для оперативного
природоресурсного и экологического мониторинга окружающей среды // II Международная периодическая научно-практическая конференция
«Альянс наук: ученый – ученому», 3-7 октября
28.
Растригин Л.А.,
Маджаров Н.Е. Введение в идентификацию объектов управления. М.: Энергия,
1977.
29. http://www.khai.edu/niipfm/russian/berkut-ru - Разведывательный беспилотный комплекс
«Беркут».
30.
Вязгин В.А., Федоров В.В.
Математические методы автоматизированного проектирования. М.: Высш. шк., 1989.
31.
Зосімович М.В. Структурно-параметрична оптимізація силових конструкцій
дистанційно-пілотованих літальних апаратів для оперативного природоресурсного
та екологічного моніторингу довкілля // Вісник Національного авіаційного університету.
- № 3-4 (33). – К.: НАУ, 2007. – С. 127-132.
32. Моисеев Н.Н. Неформальные процедуры и
автоматизация проектирования. – М.: Наука, 1979.
33.
Зосимович Н.В., Гаранин И.В., Самохин В.M.
Создание системы для выбора
схемы и основных параметров энергосиловых установок в составе
воздушно-космического самолета. – М.: MAИ. Tема
№203-94-07, 1996. – 3 п/л.
34.
Зосимович Н.В., Гаранин И.В., Самохин В.M. Cоздание интерактивной компьютерной программы силовой
схемы и основных параметров силовой установки аэрокосмического самолета.
- М.: МАИ. Tема №203-94-08, 1997. – 2,6 п/л.
35.
Зосимович Н.В.
Математические основы проектирования ДПЛА экологического назначения //
Стратегія розвитку України, К.: НАУ, 2006. - № 5.– C. 218-222.
36.
Евтушенко Ю.Г. Методы решения экстремальных
задач и их применение в системах оптимизации. М.: Наука, 1982.
37. Постнов В.А., Хархурим И.Я. Метод конечных
элементов в расчетах судовых конструкций. – Л.: Судостроение, 1974.– 341
с.
38. Подгорный
А.Н., Марченко Г.А., Пустынников В.Н. Основы и методы прикладной теории
упругости. – К.: Вища школа. Головное изд-во, 1981. - 328 с.
39. http://www.mai.ru/conf/aerospace/internetconf/ - Парафесь С.Г. Использование математического аппарата идентификации
конструкций в задачах проектирования летательных аппаратов // Интернет-конференция
"Авиация и космонавтика-2007".
40. Меркин Д.Р. Введение в
теорию устойчивости движения. – М.: Наука, 1980. - 272 с.