Кісельова О.М., Лозовська Л.І.

Дніпропетровський національний університет,

Дніпропетровський регіональний інститут державного управління

Економіко-математична модель неперервних задач оптимального покриття множин та її розв’язання

Вирішення багатьох економічних технічних проблем можуть бути отримані як розв’язання задачі про оптимальне покриття множини. Наприклад, проблема розміщення станцій стільникового зв'язку у випадку, коли необхідно визначити мінімально припустимий радіус дії станцій зв'язку при їхній фіксованій кількості; задача розміщення й визначення необхідної кількості станцій стільникового зв'язку із заданим радіусом дії; проблема визначення мінімально можливого радіусу розкиду води поливальною установкою з розміщенням заданої кількості цих установок на ділянці поливу; задача створення мережі штучних супутників землі, призначених для контролювання діапазону кругових орбіт; задача вибору оптимальної потужності рухових установок малої тяги й багато інші [1, 2, 3, 5].

Для побудови економіко-математичної моделі безперервних задач про покриття множин використовуються наступні поняття.

Нехай Ω – обмежене, замкнуте, вимірне по Лебегу множина в n-мірному евклідовому просторі Е_n.

Будемо називати с-кулею радіуса R із центром у точці τ_i з Е_n множини виду В(τ_i,R) = {хÎЕ_n: с(х,τ_i) ≤ R}, де с(х,τ_i) – функція визначення відстані між центром τ_i і точкою х [5].

Скажемо, що сукупність центрів τ₁,…,τ_N задає кульове покриття множини Ω с радіусом R, якщо ΩÍ В(τ_i,R).

Ясно, що радіус R покриття множини Ω, що задається центрами τ₁,…,τ_N має вигляд

R(τ^N) = с(х,τ_i), (1)

де τ^N = (τ₁,…,τ_N)Î= Е (або τ^N=(τ₁,…,τ_N)Î =Ω)...

Очевидно, що покриття множини Ω, що задає вектором τ^N і радіусом R(τ^N), обумовленим по формулі (1), є мінімальним с-кульовим покриттям, що генерується вектором τ^N, тобто ніякі с-кулі меншого радіуса із центрами в τ₁,…,τ_N не покривають Ω [2, 5].

Покриття мінімального радіуса назвемо оптимальним.

Таким чином, для відшукання оптимального покриття треба знайти величину

R(τ^N) = с(х,τ_i),

що називається радіусом оптимального покриття й вектор τ, при яких досягається значення рівне нижній грані.

Розглянемо деякі постановки безперервних задач про с-кульове покриття, слідуючи [1, 2, 5].

Задача 1 з фіксованими центрами.

Для заданої системи центрів (τ₁,…,τ_N) з Е (або з Ω^N) знайти мінімальне с-кульове покриття множини Ω, тобто знайти величину (1).

Розглянемо тепер більш складну задачу про оптимальне покриття, у якій на відміну від задачі 1 центри τ₁,…,τ_N не фіксовані, а повинні розміститися в множині Ω так, щоб одержати покриття мінімального радіусу (тобто оптимальне покриття).

Задача 2 про оптимальне обмежене з-кульове покриття.

При заданому числі N центрів τ₁,…,τ_N знайти їхнє розміщення в області Ω, що здійснює покриття множини Ω з мінімальним радіусом, тобто знайти величину

R(τ ) = с(х,τ_i), (2)

і вектор τÎΩ ÌЕ , при яких в (2) досягається мінімум.

Сформулюємо тепер задачу про оптимальне покриття, що відрізняється від задачі 2 тим, що центри τ₁,…,τ_N можуть розміщатися не на множині Ω, а у всьому просторі Е_n.

Задача 3 про оптимальне с-кульове покриття.

При заданому числі N центрів τ₁,…,τ_N знайти їхнє розміщення в Е_n, що здійснює покриття множини Ω с мінімальним радіусом, тобто знайти величину

R(τ ) = с(х,τ_i), (3)

і вектор τÎЕ , при яких в (3) досягається мінімум.

Відзначимо, що узагальненням задач 2 і 3 є задача про оптимальне покриття, у якій кожний (або всі) із центрів τ₁,…,τ_i,…,τ_N може розміщатися у відповідній множині Т_i з Е_n, що не обов'язково збігається з підмножиною Ω_i.

І, нарешті, сформулюємо задачу про покриття, що відрізняється від перших трьох задач тим, що кількість центрів τ₁,…,τ_N заздалегідь не задана.

Задача 4 про відшукання мінімальної по числу сукупності центрів покриття.

При заданому радіусі покриття R знайти мінімальну по кількості N сукупність центрів τ₁,…,τ_N, що генерує покриття компактної множини Ω.

Перераховані вище задачі про оптимальне покриття множини системою підмножин почали інтенсивно вивчатися в ХХ столітті й продовжують привертати увагу з наукової й практичної точок зору дотепер [1, 2, 3, 5].

Для безперервної задачі про оптимальне с-кульове покриття компактної множини Ω з Е_n заданою кількістю куль мінімального радіусу авторами запропонований і обґрунтований алгоритм [3], заснований на використанні методу узагальненого градієнтного спуску з розтяганням простору в напрямку різниці двох послідовних узагальнених градієнтів (r-алгоритму Шора) [4].

Для безперервної задачі про оптимальне с-кульове покриття компактної множини Ω з Е_n заданою кількістю куль мінімального радіусу авторами запропонований і обґрунтований алгоритм [3], заснований на використанні методу узагальненого градієнтного спуску з розтяганням простору в напрямку різниці двох послідовних узагальнених градієнтів (r-алгоритму Шора) [4].

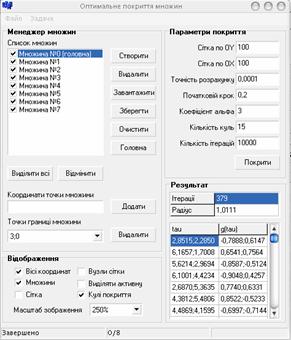
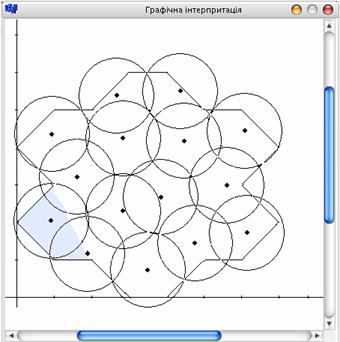
Рис. 1. Діалогове вікно роботи з програмою ОПМ.	Рис. 2. Оптимальне покриття множини для 15 центрів

Запропонований алгоритм має наступні характеристики:

- одночасно знаходить всі центри оптимального покриття;

- може бути використаний для покриття множини з n-мірного евклідового простору довільної розмірності;

- його реалізація не пов'язана з геометричними особливостями множини, що покривається;

- може бути використаний для покриття як опуклих, так і неопуклих множин, для розв’язання дискретних задач оптимального покриття, а також для розв’язання задачі покриття множини мінімальною кількістю куль заданого радіуса;

- може бути використаний для покриття множин з нерівномірно розподіленою щільністю.

Взагалі, алгоритм знаходить локальне оптимальне розв’язання задачі про оптимальне с-кульове покриття. Але, як правило, у результаті чисельних експериментів алгоритм приводив до глобального оптимального розв’язку.

Розроблений алгоритм дозволяє одержати результати для довільної кількості куль покриття. Але, як встановлено в результаті чисельних експериментів, зі збільшенням кількості куль покриття може збільшуватися й відносна похибка, з якою отримані оптимальні рішення.

Алгоритм реалізований мовою С++. На рис. 1 наведене діалогове вікно програми, результати роботи алгоритму виводяться в відповідні поля на формі, вікно графічної інтерпретації та у файл, що зберігається на диску. На рис. 2 наведено приклад оптимального покриття невипуклої множини. У результаті чисельних експериментів підтверджена порівняльна простота завдання початкових даних і висока ефективність алгоритму, а також установлено, що алгоритм добре працює з будь-якого початкового наближення для центрів покриття. Вірогідність чисельних результатів підтверджена або збігом із уже відомими як експериментальними, так і теоретичними результатами, або геометричними міркуваннями для нових модельних задач.

Список літератури

1. Брусов В.С., Пиявский С.А. Вычислительный алгоритм оптимального покрытия областей плоскости. – Журнал вычислительной математики и математической физики. – 1971. – Т.11, №2. – С.304-312.

2. Jandl H., Wieder K. A continuous Set Covering Problemas a Quasidifferentiable Optimization Problem. – Optimization 19. – (1988)6. – P.781-802.

3. Киселева Е.М., Шор Н.З. Непрерывные задачи оптимального разбиения множеств: тория, алгоритмы, приложения. – К.: Наукова думка, 2005.-564 с.

4. Шор Н.З. Методы минимизации недифференцируемых функций и их приложение. – К.: Наукова Думка. – 1979. – 199с.

5. Сухарев А.Г. Минимаксные алгоритмы в задачах целочисленного анализа. –М.: Наука. – 1989. – 300с.