Математика/1. Дифференциальные и интегральные уравнения

К.ф.-м.н. Скрыпник С.В., Саркисьянц Е.В.

Донецкий национальный университет экономики и торговли

Связь двух линейных инвариантных соотношений для задачи Кирхгоффа и для задачи о движении тела

в жидкости

Рассмотрена обобщенная задача о движении гиростата в поле потенциальных и гироскопических сил

	(1)
	(2)

Эти уравнения имеют три первых интеграла

, , .

(3)

Здесь введены следующие обозначения: – вектор угловой скорости гиростата; – единичный вектор, характеризующий ось симметрии силового поля; – гиростатический момент, определяющий внутренние движения гиростата; – вектор обобщенного центра масс; – тензор инерции гиростата, построенный в неподвижной точке; и – симметрические матрицы третьего порядка; точка над переменными обозначает относительную производную.

Ставится задача исследования условий существования у системы (1), (2) инвариантных соотношений

, , ,

где – произвольная постоянная, , – аналитические функции компонент вектора .

Получены условия на параметры. Получено, что третья координатная ось является главной в гиростате, так как одно из условий .

Далее рассмотрен случай квадратичных инвариантных соотношений. Система координат выбрана так, чтобы

,

.

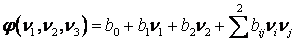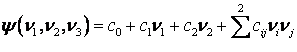Показано, что функции и не могут содержать нелинейных по слагаемых.

Рассмотрена более общая постановка задачи инвариантных соотношений в общем виде.

Если оставаться в рамках задачи (1), (2), то существенных упрощений вида инвариантных соотношений получить не удается. Поэтому использовалась гидродинамическая аналогия и рассмотрена задача о движении твердого тела в жидкости.

Если в этой задаче сделать некоторые переобозначения, то уравнения движения тела в жидкости преобразуются в уравнения Кирхгоффа. Далее был сделан перенос результатов работ П.В.Харламова в задачу о движении гиростата, вследствие чего значительно упростились условия на параметры.

Рассмотрены все случаи равенства нулю компонент вектора гиростатического момента. Получен дополнительный интеграл

,

(4)

где – произвольная постоянная.

Применение этого интеграла вместо интеграла энергии из (3) позволило упростить процедуру сведения задачи к квадратурам. Это дало возможность получить решение в эллиптических функциях времени.

В случае также имеет место дополнительный интеграл

,

где – произвольная постоянная.

Проблема сведения задачи к квадратурам связана с разрешимостью уравнения четвертой степени. В задаче о движении тела в жидкости этот факт установлен П.В.Харламовым [1]. Им указана схема сведения без получения разрешимых в явном виде случаев.

В докладе исследуется возможность получения зависимостей основных переменных от времени (указано два явных варианта сведения задачи к квадратурам).

Таким образом, использовав гидродинамическую аналогию, указаны некоторые дополнительные свойства в характере сведения задачи к квадратурам в виде дополнительных интегралов. Сопоставление условий на параметры позволило сделать вывод:

1. Если , , то имеем регулярную прецессию гиростата.

2. Если , , имеет место дополнительный интеграл (4) (задача сведена к квадратурам П.В.Харламовым [1]).

3. Если , или , , то основные переменные можно представить эллиптическими функциями времени.

Литература:

1. Харламов П.В. О решениях уравнений динамики твердого тела // Прикладная математика и механика.–1965.–Т.29, Вып.3.–с.567-572.
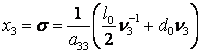