Математика/3.Теорія ймовірностей і математична статистика

Кубайчук О.О.

Європейський університет

АСИМПТОТИКА ОЦІНКИ ДЛЯ БАЄСОВОГО ПОРОГУ

Розглядається задача класифікації деякого об’єкту за спостереженням його числової характеристики . Вважаємо, що об’єкт може належати лише одному з двох класів. Розглядаємо порогові класифікатори вигляду

тобто об’єкт відносять до першого класу, якщо його характеристика потрапляє в проміжок і до другого класу в іншому випадку. Приклад такої класифікації визначення людини (об’єкт) як хворої (другий клас), якщо її температура (характеристика ) перевищує ( або рівень гемоглобіну в крові перевищує 84 одиниці) (поріг ) і є меншою за (рівень гемоглобіну є меншим за 72 одиниці) (поріг ). Можливий також варіант

Найкращим (баєсовим) вважають поріг , при якому має найменшу ймовірність помилки. Об’єкт , у якого спостерігається деяка числова характеристика , може належати одному з двох класів; невідомий номер класу, якому належить позначимо . Вважаються відомими апріорні ймовірності , . Характеристика – випадкова, її розподіл залежить від : . Розподіли невідомі, але будемо вважати, що вони мають неперервні щільності відносно міри Лебега .

Методи оцінки і основні результати

Множину всіх класифікаторів позначимо . Ймовірність помилки класифікатора:

Баєсовим класифікатором у класі називають класифікатор , на якому досягається мінімум :

.

Поріг баєсового класифікатора є баєсовим порогом: .

Для маємо:

де

, .

Для маємо:

де

, .

Найкращим (баєсовим) вважають поріг , при якому має найменшу ймовірність помилки. При цьому виникає проблема вибору (оцінки) порогу на основі навчаючої вибірки. Найбільш поширеними методами оцінювання за повністю класифікованою вибіркою є емпірично-баєсова класифікація (ЕБК) [3;5] та метод мінімізації емпіричного ризику (МЕР) [2;7].

Розглянемо перший метод. Вважаємо, що навчаюча вибірка отримана із суміші зі змінними концентраціями. Будемо досліджувати асимптотичну поведінку цього методу.

Розглянемо випадок . Функції (а, значить, і ) вважаються невідомими. Їх можна оцінити за даними, що являють собою вибірку із суміші зі змінними концентраціями: , – незалежні між собою при фіксованому і , де – відома концентрація об’єктів першого класу у суміші в момент -го спостереження [6]. Для оцінки функції розподілу використовують зважені емпіричні функції розподілу

,

де – індикатор події , – вагові коефіцієнти:

, ,

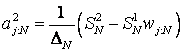(див. [6]).

Для оцінки щільностей розподілів можна скористатися ядерними оцінками

,

де – ядро (щільність деякого ймовірнісного розподілу), – параметр згладжування [1;4].

Оцінка ЕБК будується наступним чином: знаходиться множина всіх розв’язків рівняння і на роль оцінки використовується , де

,

, ;

, .

Будемо вважати, що виконуються наступні умови:

(А). існує і є єдиною точкою глобального мінімуму ( є точкою глобального мінімуму , – ).

(). Існують границі , і .

Теорема 1. Нехай виконуються (А), (), існують і є неперервними щільності , , , – неперервна функція

.

Тоді ( , ) за ймовірністю при .

Далі оцінку порогу будуємо методом мінімізації емпіричного ризику. Знову вважаємо, що навчаюча вибірка отримана із суміші зі змінними концентраціями. Припущення щодо оцінок для і такі ж як і раніше. Дослідимо асимптотичну поведінку цього методу. Оцінка МЕР визначається як , де

,

де

, .

Отже, , . Будемо вважати, що виконуються наступні умови:

(А). існує і є єдиною точкою глобального мінімуму .

(). Існують границі , і .

Теорема 2. Нехай виконуються (А), (), – неперервні функції на . Тоді (, ) за ймовірністю при .

Висновки

В даній роботі знайдено умови збіжності за ймовірністю оцінок для баєсового порогу, побудованих методом мінімізації емпіричного ризику і методом емпірично-баєсової класифікації для вибірки із суміші зі змінними концентраціями.

Література:

1. Биллингсли П. Сходимость вероятностных мер. – М., 1977.

2. Вапник В.Н. Индуктивные принципы поиска эмпирических закономерностей // Распознавание . Классификация. Прогноз, Вып.1. – М., 1989.

3. Деврой Л., Дьерфи Л. Непараметрическое оценивание плотности. – М., 1988.

4. Іванько Ю.О. Асимптотика ядерних оцінок щільностей та їх похідних, побудованих за спостереженнями із суміші зі змінними концентраціями // Вісник КНУ, сер. Математика. Механіка. – 2003. – №9. – С. 29–35.

5. Іванько Ю.О., Майборода Р.Є. Експоненціальні оцінки емпірично-баєсового ризику при класифікації суміші зі змінними концентраціями // Український математичний журнал. – 2002. – Т.54, №10. – С. 1421–1428.

6. Майборода Р.Є. Статистичний аналіз сумішей. – К., 2003. 7. Vapnik V.N. The nature of Statistical Learning Theory. – N. Y., 1996.