К.т.н. Болоткин С.Н., к.т.н. Судариков А.Е.

Карагандинский государственный технический университет

РАСЧЕТ КАМЕННЫХ КОНСТРУКЦИЙ НА ПРОЧНОСТЬ ПРИ ПРОДОЛЬНОМ ИЗГИБЕ НА ЦЕНТРАЛЬНОЕ И ВНЕЦЕНТРЕННОЕ НАГРУЖЕНИЕ

В настоящее время расчет каменных конструкций на продольный изгиб производится на основе экспериментальных данных, результаты которых часто экстраполируются на условия, где экспериментальных данных не имеется, особенно для высоких стенок, так как нет единого теоретического подхода для решения подобных задач.

Однако такое решение может быть получено, если предположить, что предельной нагрузкой является такая, при которой происходит прогиб конструкции, и на вогнутой грани сечения напряжения сжатия достигают предела прочности материала- R[1,2].

Исходя из этого положения, можно составить условие предельного равновесия (рис 1.)

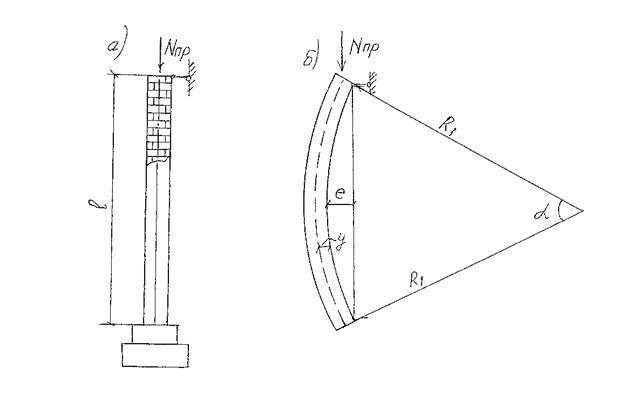
Рисунок 1. а) Заданная система;

б) Расчетная схема кладки при продольном изгибе

(1)

где: R - прочность кладки на сжатие,

- предельная продольная сила,

А - площадь сечения элемента

е - эксцентриситет, возникший вследствие продольного изгиба

W-момент сопротивления элемента кладки

Решая (1) относительно N_пp получим

(2)

Для нахождения N_пp имеем

(3)

где l - высота стенки,

- начальный модуль упругости кладки [3]

Начальный модуль упругости кладки определится как

(4)

где:

-упругая характеристика кладки.

Тогда предельно минимальный радиус кривизны кладки (рис. l) R определится из соотношения

(5)

где у - расстояние от центра тяжести сечения элемента до сжатой грани.

Центральный угол при дуге радиуса составит

(6)

Эксцентриситет приложения силы относительно сжатой грани - е

(7)

Для элементов кладки таврового сечения продольный изгиб происходит в сторону минимального расстояния от центра тяжести сечения до сжатой грани, т.е в сторону - Поэтому (5) принимает вид

(8)

Центральный угол при дуге радиуса

(9)

Длина хорды при дуге радиуса

(10)

Эксцентриситет силы относительно вогнутой грани сечения

е = R_шiп • [1- cos(a /2)]; (11)

Для внецентренно нагруженной неармированной кладки (рис.2) имеем следующее условие равновесия на вогнутой грани сечения,

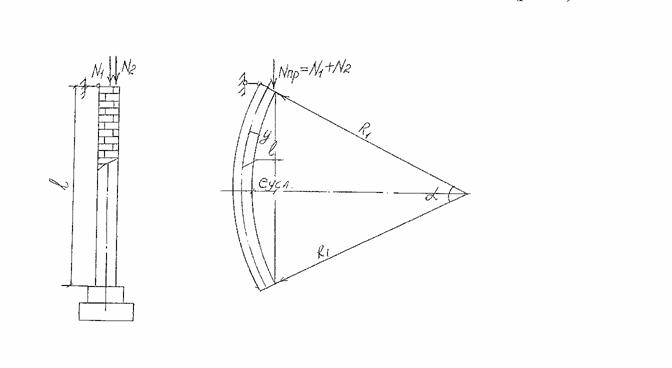
Рисунок 2. а) заданная система; б) расчетная схема для определения эксцентриситета приложения N_пp при внецентренном нагружении кладки

; (12)

где N_пp - предельная продольная сила, равная сумме продольных сил,

е - предельный прогиб для центрально сжатой кладки, определяемый по (8),

е_усл, - условный эксцентриситет. При замене отдельных продольных сил

эквивалентной условной силой - N_пp , условный эксцентриситет равен

(13)

где W - момент сопротивления элемента сечения кладки.

Для элементов кладки таврового сечения радиус кривизны элементов кладки - определяется по (5), центральный угол при дуге радиуса по (6), длина хорды по (7), эксцентриситет е по (8), (рис.1б).

Для элементов кладки с сетчатым армированием расчетная прочность кладки рассчитывается при растворах марки 25 и выше как [3]

(14)

где Rs - расчетное сопротивление неармированной кладки,

- объемный процент армирования = (V_s / V_k) ·100,

где - объем арматуры,

V_k - объем кладки (принимается в пределах 0,1-1%)

100 - расчетное сопротивление армированной кладки.

При кладке на растворах марки менее 25

(15)

где - расчетное сопротивление клади на растворе марки 25.

Но не должно быть более 1,8 R.

Начальный модуль упругости для кладки с сетчатым армированием принимается как для неармированной кладки. Дальнейший расчет кладки прямоугольного и таврового сечения на центральное и внецентренное нагружения производится по тем же формулам, что и для неармированной кладки, но расчетная прочность кладки принимается по (15).

Но при этом надо учитывать, что при приведенной гибкости > 15 или > 53 применение сетчатого армирования не повышает прочность кладки. Элементы кладки с продольным армированием по своей работе аналогичны железобетонным элементам, работающим на продольный изгиб. В этом случае каменная кладка исполняет роль бетона. Поэтому для расчета каменной кладки на центральное и внецентренное нагружение могут быть использованы решения, полученные в работе [1]. Для этого площадь сечения элемента кладки с продольной арматурой заменяется площадью приведенной к кладке как

(16)

где А - площадь сечения элемента кладки,

v - отношение модулей упругости арматуры и кладки,

и - площади сечения условно растянутой и условно сжатой арматуры, приведенные к кладке.

Дальнейший расчет продольно армированной кладки на центральное и внецентренное нагружение аналогичен расчету неармированной кладки.

Предлагаемый метод расчета каменных конструкций хорошо согласуется с принятым методом расчета каменных конструкций на центральное и внецентренное сжатие, не требует введения эмпирических коэффициентов и основан на едином принципе, что предельной нагрузкой при продольном изгибе является достижение предельных напряжений на изогнутой грани сечения. Поэтому принцип расчета каменных конструкций описывается аналогичными формулами [1,2] как для каменных конструкций, так и для железобетонных конструкций и стальных колонн, работающих на продольный изгиб.

ЛИТЕРАТУРА:

1. Болоткин С.Н. Расчет железобетонных колонн на прочность при продольном изгибе на центральное и внецентренное нагружение. Карагандинский государственный технический университет. Труды университета, вып.2, Караганда, 1997.

2. Болоткин С.Н Расчет стальных колонн на прочность при центральном и внецентренном нагружении. Материалы 111 международной научно-технической конференции "Научное пространство Европы".Том 10, г. Днепропетровск, " Наука и образование", 2007

3. Жилые и общественные здания. Краткий справочник инженера-конструктора. Под редакцией проф. Ю.А. Дыховичного, М.,1991.