Технические науки/ 3. Отраслевое машиностроение

К.т.н. Гурьянов Г.А., Васильева О.Ю.

Восточно-Казахстанский государственный технический университет им. Д Серикбаева, Республика Казахстан

Определение плеча действия реактивной силы для получения оптимального скоростного режима роторов реактивных центрифуг

Для вращения ротора центробежного очистителя при его установке в гидросистемах машин удобным является применение реактивного привода.

Эффективность работы любой центрифуги в большой степени зависит от силовых параметров ее привода - мощности и крутящего момента. При этом весьма важным вопросом является определение оптимального радиуса расположения сопел (оптимального плеча действия реактивной силы).

Существуют формулы для определения оптимального плеча действия реактивной силы в зависимости от расхода жидкости /1/, /2/. Но так как в гидросистемах ограничено главным образом давление рабочей жидкости, а не ее расход, то оптимальное плечо действия реактивной силы целесообразнее определять в зависимости от давления жидкости перед центрифугой. Поскольку существующие способы определения оптимального радиуса расположения сопел в зависимости от давления сложны и мало пригодны для практического использования, постольку сохраняет актуальность задача получения достаточно простой математической зависимости для определения оптимального плеча действия реактивной силы.

Сначала найдем выражение для определения крутящего момента от реактивных сил, создаваемых струей жидкости, вытекающей из сопел, и приводящих ротор во вращение. Крутящий момент в общем виде выражается:

, Н×м, (1)

где R – реактивная сила струи, вытекающей из сопла, Н; r_с – плечо действия реактивной силы, равное расстоянию от оси вращения до оси сопла, м.

Определив выражение для реактивной силы в зависимости от давления и подставив его в формулу (1), после преобразований получим достаточно простую и пригодную для практического использования зависимость крутящего момента от давления жидкости в гидросистеме перед очистителем:

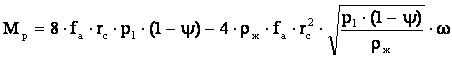, Н×м, (2)

где f_a – площадь отверстий сопел, м²; r_с – плечо действия реактивной силы, м; р₁ – давление рабочей жидкости перед очистителем, Па; y - коэффициент потерь давления; r_ж – плотность рабочей жидкости, кг/м³; w - угловая скорость вращения ротора, с^-1.

Анализ уравнения (2) показывает, что уменьшение радиуса расположения сопел приводит к уменьшению величины крутящего момента. Поэтому необходимо подобрать такое оптимальное значение радиуса расположения сопел (плеча действия реактивной силы) r_с^опт, чтобы при высоком крутящем моменте обеспечивалась также и максимальная частота вращения ротора.

Для нахождения оптимального радиуса расположения сопел получим выражение для определения частоты вращения ротора центрифуги.

Частоту вращения ротора найдем из условия равенства момента крутящего и суммарного момента сопротивления вращению ротора М_с (Н×м):

, Н×м, (13)

Суммарный момент сопротивлений определим по методике М.А.Григорьева и Г.П.Покровского /1/ через обобщающие коэффициенты, найденные эмпирическим путем, что несколько снижает точность вычислений, но значительно их упрощает. Выражение в этом случае имеет вид:

, Н×м, (14)

где а – момент сопротивления при начале вращения ротора, Н×м; b – скорость нарастания момента сопротивления, Н×м/(об/мин); n - частота вращения ротора, об/мин.

Эмпирические формулы, для определения коэффициентов а и b:

, Н×м , Н×м/(об/мин) (16)

где W - емкость ротора, м³; m - динамический коэффициент вязкости, Па×с.

Подставим в формулу (13) выражения для крутящего момента (12) и момента сопротивлений (14), заменяя в формуле (12) угловую скорость w, с^-1, на частоту вращения n, об/мин, согласно следующего равенства , м/с, после подстановок и преобразований получим формулу для вычисления частоты вращения ротора центрифуги:

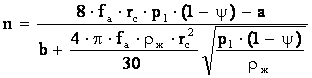, об/мин (19)

Чтобы получить формулу для определения оптимального радиуса расположения сопел продифференцируем полученное уравнение (19) по dr_c и приравняем нулю производную, dn/dr_c=0. После преобразований получим выражение для определения оптимального радиуса расположения сопел ротора центрифуги в зависимости от давления:

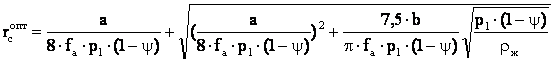, м, (20)

где значения а и b определяются по формулам (15) и (16).

Решение полученного итогового уравнения (20) не представляет особых трудностей, что позволяет достаточно легко определять оптимальный радиус расположения сопел при проектировании и эксплуатации центрифуг с реактивным приводом. Но окончательный вывод о пригодности полученной формулы для инженерных расчетов можно сделать лишь после экспериментальной проверки.

Литература:

1 Григорьев М.А., Покровский Г.П. Автомобильные и тракторные центрифуги. М. МАШГИЗ, 1961, 184с.

2 Завьялов Л.Л. Расчет скоростного режима роторов автомобильных и тракторных центрифуг // Труды всесоюзного совещания. М.: ОНТЭИ., 1973.