Ташатов Н.Н.

 

Евразийский национальный университет им. Л.Н. Гумилева, г. Астана

 

систематические и несистематические сверточные коды и распространение катастрофических ошибок

 

Систематический сверточный код – это код, в котором входной k-кортеж представляет как часть выходного n-кортежа кодового слова, соответствующего этому k-кортежу. На рисунке 1 показан двоичный систематический кодер со степенью кодирования   и K = 3.

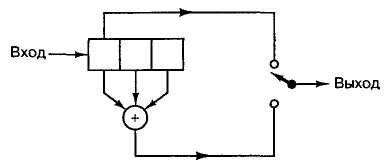
Рисунок 1 – Систематический сверточный кодер степенью

кодирования 1/2 и длиной кодового ограничения  K = 3

 

Любой несистематический код, для линейных блочных кодов, можно преобра­зовать в систематический с такими же пространственными характеристиками блоков. При использовании сверточных кодов это преобразование невозможно. Причина в том, что сверточные ко­ды сильно зависят от просвета [1, 2, 3].

Определение. Минимальная длина пути из числа расходящихся, а затем сливающихся путей называется минимальным просветом  или просто просветом.

При построении сверточного кода в систематической форме при данной длине кодового ограничения и степени кодирования максимально возможное значение просвета снижается.

В таблице 1 показан максимальный просвет для сис­тематического и несистематического кодов при степени кодирования  с K от 2 до 8. При большой длине кодо­вого ограничения результаты отличаются еще сильнее [4].

 

Сравнение систематического и несистематического просветов,

степень кодирования 1/2

Таблица 1.

Длина кодового ограничения

Просвет

систематического кода

Просвет несистематического кода

2

3

3

3

4

5

4

4

6

5

5

7

6

6

8

7

6

10

8

7

10

 

Распространение катастрофических ошибок в сверточных кодах

Когда конечное число ошибок в кодовых симво­лах вызывает бесконечное число битовых ошибок в декодированных данных, возникает катастрофическая ошибка. Мэсси(Massey) и Сейн (Sain) указали необходимые и достаточные условия для сверточного кода, при которых возможно распространение катастрофических ошибок. Условием распространения катастрофических ошибок для кода со степенью кодирования 1/2, реализованного на полиномиальных генераторах [3], будет на­личие у генераторов общего множителя многочленов (степени не менее едини­цы). Например, на рисунке 2, а показан кодер с K = 3, степенью кодирования 1/2, со старшим многочленом g1(X) и младшим g2(X)

 

                                                   (1)

Многочлены  g1(X) и  g2(X) имеют общий множитель многочленов 1 + X, т.к.

1 + X 2  = (1 + X)(1 + X)

Следовательно, в кодере, (рисунок 2 а), может происходить распростра­нение катастрофической ошибки.

         Если рассматривать диаграмму состояний кода произвольной степени кодирования, то катастрофическая ошибка может появиться тогда и только тогда, когда любая петля пути на диаграмме имеет нулевой весовой коэффициент, т.е. нулевое расстояние до нуле­вого пути. Чтобы проиллюстрировать это, рассмотрим пример, приведенный на рисунке 2 б. Т.к. петля в узле a не дает никакого вклада в пространственные характеристики последовательности кодовых слов относительно нуле­вой последовательности, то ее можно убрать. Более того, узел a разбиваем на два узла, один из них представляет вход, а другой – выход диаграммы состояний. Обозначим их  через а и е. Все  пути,  начинаются  из  состояния  a = 00 и заканчиваются в  е = 00. Переда­точную функцию T(D) пути abce, который начинается и заканчивается в состоянии 00, можно вычислить через неопределенный «заполнитель» D как D2DD2 = D5, где степень D общее число единиц на пути, т.е. расстояние Хэмминга до нулевого пути. Точно так же пути abdce и abcbce имеют передаточную функцию D6 и, соответст­венно, расстояние Хэмминга, равное 6, до нулевого пути. Допустим, что нулевой путь является правильным, тогда неправильный путь abdd ... dee имеет точно 6 единиц, независимо от того, сколько раз мы обой­дем вокруг петли в узле  d.

 

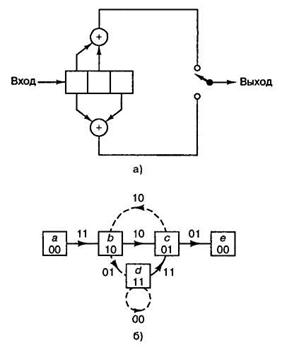
Рисунок  2 – Кодер, в котором возможно накопление

катастрофической ошибки: а) кодер; б) диаграмма состояний

 

Поэтому, например, для канала BSC (двоичный симметричный канал) к выбору этого непра­вильного пути могут привести три канальные ошибки. На таком пути может появиться сколь угодно большое число ошибок (две плюс количество обхода петли). Для кодов со степенью кодирования  можно видеть, что если каждый сумматор в кодере имеет четное количество соединений, петли, которые соответствуют информа­ционным состояниям со всеми единицами, будут иметь нулевой вес, отсюда следует, что код будет катастрофическим.

Единственное преимущество описанного ранее систематического кода заключается в том, что он никогда не будет катастрофическим, т.к. каждая петля должна содержать, по крайней мере, одну ветвь, порождаемую ненулевым входным битом. Следова­тельно, каждая петля должна содержать ненулевой кодовый символ.

 

 

Границы рабочих характеристик сверточных кодов

Передаточную функцию кода T(D), иногда называют производящей функцией кода. Вычисляется по формуле .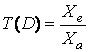

С помощью передаточной функции кода можно получить более подробную информацию, чем при использовании лишь расстояния между различными путями. В каждую ветвь диаграммы состояний введем множитель L так, чтобы этот показатель L мог служить счетчиком ветвей в любом пути из состояния  a = 00 в состояние e = 00.

Введем также множитель N  во все ветви переходов, порожденных входной двоичной единицей. Таким образом, после прохождения ветви суммарный множитель N возрастает на единицу, если только этот переход ветви вызван входной битовой единицей. Для сверточного кода, (рисунок 1), на перестроенной диаграмме состояний (рисунок 3) показаны дополнительные множители L и N.

 

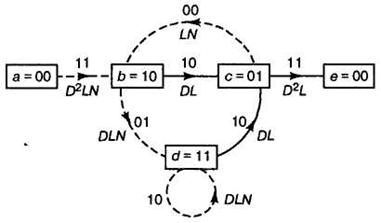
Рисунок 3 – Диаграмма  состояний с обозначением расстояния,

длины и числа входных единиц

 

Уравнения состоя­ния  вычисляются следующим образом:

 

                                        (2)

Тогда передаточная функция кода такой доработанной диаграммы состояний будет иметь следующий вид [1, 2]:

     (3)

Вероятность битовой ошибки Pb в бинарном сверточном ко­де, использующем при декодировании жесткую схему принятия решений, может быть ограничена сверху следующим образом [5]:

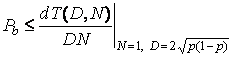,                              (4)

где р – вероятность  ошибки в канальном символе. Передаточная функция T(D, N) получено из  T(D, L, N)  при  L = 1 в уравнении (3).

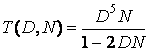,                                           (5)

тогда

.                                    (6)

Объединяя уравнения (5) и (6), запишем следующее:

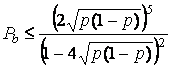.                                            (7)

При когерентной модуляции BPSK в канале с аддитивным белым гауссовым шумом (AWGN) вероятность битовой ошибки ограничивается следующей величиной:

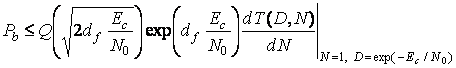.       (8)

где .

 – отношение энергии информационного бита к спектральной плотности мощности шума,

 – отношение энергии канального символа к спектральной плотности мощности шума,

 – степень кодирования,

Q(x) – гауссов интеграл ошибок и определяется уравнением 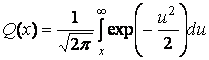 и приведен в [1, таблица Б.1]. Следователь­но, для кода со степенью кодирования 1/2 и просветом df = 5, при использовании когерентной схемы BPSK и жесткой схемы принятия решений при декодировании, мо­жно записать следующее:

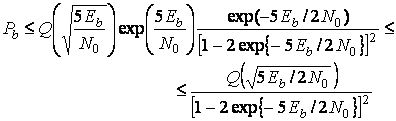 .                  (9)

 

СПИСОК ЛИТЕРАТУРЫ

 

1.     Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е, испр.: Пер. с англ. – Издательский дом «Вильямс», 2004. – 1104 с. ил.

2.     Вернер М. Основы кодирования. Москва: Техносфера, 2004. – 288 с.

3.     Ташатов Н.Н. Представление сверточного кодера. // в печати.

4.     Viterbi A. J. and Omura J. К. Principles of Digital Communication and Coding, McGraw-Hill Book Company, New-York, 1979, p. 251.

5.     Viterbi A. Convolutional Codes and Their Perfomance in Communication Systems. IEEE Trans. Commun. Technol., vol. COM19, n. 5, October, 1971, pp. 751-772.