Городецький В.В., Ленюк О.М.

Чернівецький національний університет імені Юрія Федьковича

Двоточкова задача для еволюційних рівнянь з

псевдо-Бесселевими операторами

Останнім часом інтенсивно розвивається теорія псевдодиферен-ціальних операторів (ПДО), які формально можна подати у вигляді , де – функція (символ), що задовольняє певні умови, – пряме та обернене перетворення Фур’є.

До псевдодиференціальних рівнянь формально можна віднести і сингулярні еволюційні рівняння з оператором Бесселя , який визначається за допомогою співвідношення , де – перетворення Бесселя, – елемент простору, в якому вказане перетворення визначене. До класу псевдодиференціальних рівнянь природно віднести еволюційні рівняння з оператором , де – деякий однорідний негладкий у точці 0 символ ( надалі називатимемо псевдо-Бесселевим оператором). Для таких рівнянь задача Коші та двоточкова задача не вивчені.

У цій праці встановлюється коректна розв’язність двоточкової задачі для рівняння

у випадку, коли крайова умова є узагальненою функцією типу розподілів. Досліджується структура фундаментального розв’язку такої задачі, знайдено умови, за яких розв’язок подається у вигляді згортки крайової умови та фундаментального розв’язку.

Нехай , Т – фіксоване додатне число, – фіксоване число з множини , – фіксоване число, .

Символом Ф позначимо сукупність функцій , парних по змінній , які задовольняють нерівності

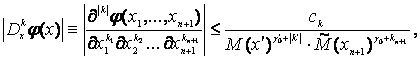
Ф – повний досконалий зліченно нормований простір, збіжність у якому вводиться стандартним чином [1].

У Ф визначена і неперервна операція зсуву аргументу по змінних , тобто

а також операція узагальненого зсуву аргументу по змінній :

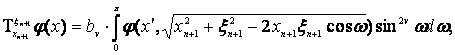
ця операція відповідає оператору Бесселя , якій діє по змінній [1].

На елементах простору Ф визначена і є неперервною операція перетворення Фур’є-Бесселя, яку надалі позначатимемо символом :

(тут – нормована функція Бесселя).

Символом позначимо простір усіх лінійних неперервних функціоналів над відповідним простором основних функцій зі слабкою збіжністю. Оскільки в просторі Ф визначена операція зсуву аргументу та операція узагальненого зсуву аргументу, то згортку узагальненої функції з основною функцією задамо формулою

де при цьому є нескінченно диференційовною функцією. Якщо і із співвідношення у просторі Ф випливає, що у просторі Ф то функціонал називається згортувачем у просторі Ф.

Перетворення Фур’є-Бесселя узагальненої функції визначимо за допомогою співвідношення

– обернене перетворення Фур’є-Бесселя:

де . Для перетворення Фур’є-Бесселя узагальнених функцій з простору правильним є наступне твердження: якщо узагальнена функція – згортувач у просторі Ф, то для довільної основної функції .

Нехай – неперервна, парна по змінній функція, однорідна порядку (тобто ), яка:

1) нескінченно диференційовна при ;

2) похідні функції задовольняють умову

3) .

Зазначимо, що функція є мультиплікатором у просторі . У зв’язку з цим розглянемо оператор , який визначимо за допомогою співвідношення

Із властивостей перетворення Фур’є-Бесселя (прямого і оберненого) випливає, що – лінійний і неперервний оператор у просторі Ф.

Розглянемо двоточкову задачу

(1)

(2)

(тут вважаємо, що ). Класичний розв’язок задачі (1), (2) шукаємо за допомогою перетворення Фур’є-Бесселя, тому припускаємо, що функція є елементом простору Ф. За допомогою безпосередніх обчислень знаходимо, що розв’язок задачі (1), (2) має вигляд

Тут

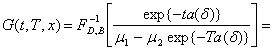
(3)

Для функції правильними є наступні оцінки:

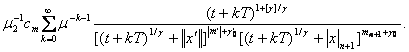(4)

Зауваження 1. Із оцінок (4) похідних функції випливає, що при кожному функція , як функція аргументу , є елементом простору Ф.

Оскільки

то

Лема 1. при у просторі .

Лема 2. при у просторі .

Надалі функцію називатимемо фундаментальним розв’язком двоточкової задачі (задачі Діріхле) для рівняння (1).

Наслідок 1. Нехай

.

Тоді граничні співвідношення

виконуються у просторі .

Для рівняння (1) двоточкову задачу (задачу Діріхле) поставимо так:

(5)

де . Під розв’язком задачі (1), (5) розумітимемо функцію , яка задовольняє рівняння (1), а також крайову умову (5) у тому сенсі, що

(границі розглядаються у просторі ). Символом позначимо сукупність усіх узагальнених функцій з простору , які є згортувачами у просторі Ф.

Теорема. Задача (1), (5) коректно розв’язна в класі узагальнених функцій . Розв’язок подається у вигляді згортки:

де – фундаментальний розв’язок двоточкової задачі для рівняння (1), визначений формулою (3).

Література

1. Ленюк О.М. Перетворення Бесселя одного класу узагальнених функцій типу розподілів // Науковий вісник Чернівецького університету: Збірник наук. праць. Вип. 336-337. Математика. – Чернівці: Рута, 2007. – С. 95 – 102.