Ленюк¹ М.П., Шинкарик² М.І.

¹ Чернівецький національний університет імені Юрія Федьковича,

² Тернопільський державний економічний університет

Обчислення невласних інтегралів методом інтегрального перетворення Ейлера на полярній вісі та сегменті [0, R]

І. Побудуємо обмежений на полярній вісі = {r: r Î (0, ¥)} розв’язок диференціального рівняння Ейлера 2-го порядку

(B_a – q²)u(r) = –g(r), q > 0, r Î (0, ¥). (1)

Тут B_a – диференціальний оператор Ейлера [1]

B_a = r²d²/dr² + (2a + 1)rd/dr + a², 2a + 1 > 0.

Фундаментальну систему розв’язків для диференціального рівняння Ейлера (B_a – q²)v = 0 утворюють функції r^{–a + q} та r^{–a – q} [1].

Якщо g(0) = const < ¥, g(¥) = const < ¥, то обмеженим розв’язком крайової задачі (1) є функція

u(r) = 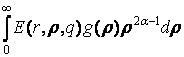. (2)

У формулі (2) бере участь функція Коші

E(r, r, q) = 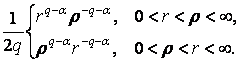(3)

Запровадимо інтегральне перетворення, породжене на множині диференціальним оператором Ейлера B_a [2]:

H_a[g(r)] = 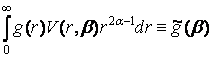, (4)

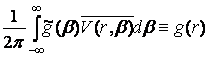= , (5)

H_a[B_a[g(r)]] = . (6)

У рівностях (4), (5) бере участь функція V(r, b) = r^–a r^–ib як розв’язок диференціального рівняння Ейлера (B_a + b²)V = 0, а риска зверху означає комплексне спряження.

Застосуємо до задачі (1) оператор H_a за правилом (4). Внаслідок тотожності (6) маємо алгебраїчне рівняння

(b² + q²).

Звідси одержуємо

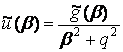. (7)

Застосувавши до функції , визначеної формулою (7), оператор згідно правила (5), одержуємо єдиний розв’язок задачі (1):

u(r) = 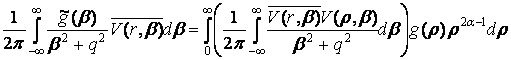. (8)

Порівнюючи розв’язки (2) та (8) в силу єдиності, маємо формулу обчислення наступного невласного інтегралу:

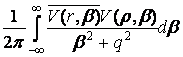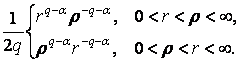= (9)

Оскільки

= (rr)^–a[cos(b ln r/ r) + i cos(b ln r/ r)],

то формула (9) набуває вигляду:

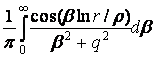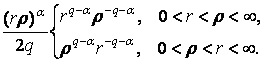= (10)

При a = 0 маємо:

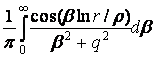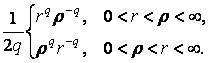= (11)

Зауважимо, що в довідковій літературі інтеграли (10), (11) відсутні.

ІІ. Побудуємо на сегменті I₁ = {r: r Î (0, R), R < ¥} полярної вісі обмежений розв’язок диференціального рівняння Ейлера 2-го порядку

(B_a – q²)u(r) = –g(r), q > 0 (12)

за крайовими умовами

= 0, . (13)

Наявність фундаментальної системи розв’язків для диференціального рівняння Ейлера (B_a – q²)v = 0 дозволяє будувати розв’язок крайової задачі (12), (13) методом функцій Коші:

u(r) = W_a(r, q)g_R + 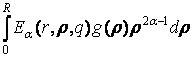. (14)

У формулі (14) беруть участь головні розв’язки даної крайової задачі:

1) породжена крайовою умовою в точці r = R функція Гріна

W_a(r, q) = , (15)

2) породжена неоднорідністю рівняння (12) фундаментальна функція крайової задачі

E_a(r, r, q) = 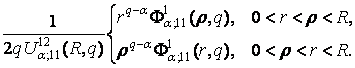(16)

У рівностях (15), (16) прийняті позначення:

,

,

.

Побудуємо тепер розв’язок крайової задачі (12), (13) методом інтегрального перетворення Ейлера, породженого на множині I₁ диференціальним оператором Ейлера B_a.

Визначимо функції

,

,

,

.

Згідно з роботою [3] запровадимо пряме H_a та обернене інтегральне перетворення, породжене на множині I₁ оператором B_a:

H_a[g(r)] = 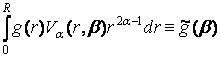, (17)

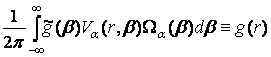= , (18)

H_a[B_a[g(r)]] = + b R^ag_R. (19)

Застосувавши до задачі (12), (13) згідно правила (17) оператор H_a, одержимо в силу тотожності (19) алгебраїчне рівняння

(b² + q²) + b R^ag_R.

Звідси знаходимо

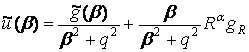. (20)

Застосуємо до функції , визначеної формулою (20), оператор за правилом (18). Після низки елементарних перетворень одержуємо єдиний розв’язок задачі (12), (13):

u(r) =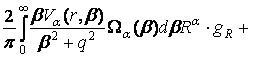

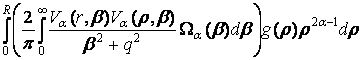+. (21)

Порівнюючи розв’язки (14) та (21) в силу єдиності, маємо формули обчислення невласних інтегралів за власними елементами диференціального оператора Ейлера B_a:

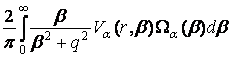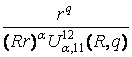= , (22)

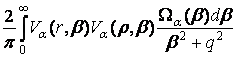= E_a(r, r, q). (23)

Функція E_a(r, r, q) визначена формулою (16).

У випадку крайової умови першого роду ( = 0, = 1) отримуємо такі невласні інтеграли

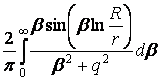= , (24)

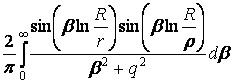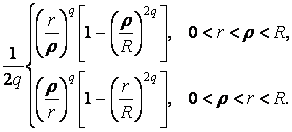= (25)

Одержані інтеграли (22) – (25) відсутні в довідниковій математичній літературі.

1. Степанов В.В. Курс дифференциальных уравнений. – М.: Физматгиз, 1959. – 468 с.

2. Снеддон И. Преобразования Фурье. – М.: Изд-во иностр. лит., 1955. – 667 с.

3. Ленюк М.П., Шинкарик М.І. Гібридні інтегральні перетворення (Фур’є, Бесселя, Лежандра). Частина 1. – Тернопіль: Економічна думка, 2004. – 368 с.