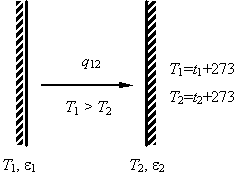http://www.rusnauka.com
Mathematics/5. Mathematical modelling
Karvatskiy A.Ya., Dudnikov P.I., Leleka S.V., Shilovich I.L., Pulinets I.V.
National technical university
of Ukraine
“Kiev
To the
consideration of radiation and complicated heat transfer problem solution by
boundary elements method
Most of the problems which can be
reduced to tasks of radiation heat exchange (further – radiation) between solid
bodies of the complete shape divided diathermic environment, have no direct
analytical decision. Usually
for such tasks solution numerical methods are used: zonal,
Monte-Carlo [1], traces of rays [2,3]. However the method of boundary elements (BEM)
can be effectively applied to problems with diffuse borders [4,5]. Complex heat
exchange problems solution, for example, stationary radiating and conductive heat transfer, without and with interaction
between bodies are most interesting in practice. Technique of numerical solution
of the conductive heat exchange problem on the basis of BEM is described in [6]. To solve the radiating
heat-conduction problem and complex heat exchange effectively
it is necessary to solve some problems connected with: calculation of radiation
influence factors for diathermic cavity surrounded by non-transparent (opaque) diffused
- reflecting borders; taking into account effect of beams shielding at influence
factors calculation; joint solution of the nonlinear equations system which describe
conductive and radiation heat
transfer. This work main objective is to develop the BEM numerical
technique and work out a software for solution of radiating and complex heat
exchange problems.
Let's
consider problem statement as follows. Let 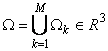 is the area which includes an ensemble of
is the area which includes an ensemble of ![]() (some industrial equipment elements
of construction) boundary lines of which are a conjugation of piecewise - flat ensembles
(some industrial equipment elements
of construction) boundary lines of which are a conjugation of piecewise - flat ensembles ![]() . So at
. So at ![]() means a solid heat-conductive
bodies, and at
means a solid heat-conductive
bodies, and at ![]() - diathermic cavities between
boundaries of which the radiation heat transfer has take place. In solid heat
conductors bodies for the account of boundary line the solid - melt is used the
generalized statement of problem. On
- diathermic cavities between
boundaries of which the radiation heat transfer has take place. In solid heat
conductors bodies for the account of boundary line the solid - melt is used the
generalized statement of problem. On ![]() boundary lines of a construction with 3-rd
types of boundary conditions (BC), and on
boundary lines of a construction with 3-rd
types of boundary conditions (BC), and on ![]() - a union of contacts between various members are observed. As on
- a union of contacts between various members are observed. As on ![]() are set various BC it also can be presented in
the form of unions:
are set various BC it also can be presented in
the form of unions: ![]() , where
, where ![]() - BC of
Dirichle,
- BC of
Dirichle, ![]() - BC of Neumann,
- BC of Neumann, ![]() - BC the convective type. To take
into account solid-melt border in solid heat conductors a generalized problem
statement is used.
- BC the convective type. To take
into account solid-melt border in solid heat conductors a generalized problem
statement is used.
In
the case of outer boundary with 3 types of
boundary conditions (BC) a definition of ![]() is applied, in the
case of
is applied, in the
case of ![]() - contacts joining between different
elements is considered.
- contacts joining between different
elements is considered.
As
at ![]() a different BC are applied it could be
considered as unification:
a different BC are applied it could be
considered as unification: ![]() , where
, where ![]() - BC Dirichle,
- BC Dirichle, ![]() - BC of Neumann,
- BC of Neumann, ![]() - BC of convective type. Due to the
existing of radiation heat transfer a
- BC of convective type. Due to the
existing of radiation heat transfer a ![]() is considered as unification:
is considered as unification: ![]() , where
, where ![]() - surface contacts between heat conductors
- surface contacts between heat conductors ![]() ,
, ![]() - surface contacts between diathermic or transparent
solid and non-transparent solid heat conductors.
- surface contacts between diathermic or transparent
solid and non-transparent solid heat conductors.
On
the base of written previously, with accounting of complete heat transfer a
temperature field in ![]() could be described by next equations set with
correspondent BC:
could be described by next equations set with
correspondent BC:
 (1)
(1)
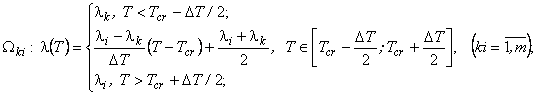 (2)
(2)
 (3)
(3)
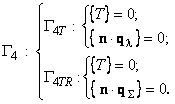 (4)
(4)
where ![]() - heat conductivity
- heat conductivity![]() , Wt/(m×Ê);
, Wt/(m×Ê); ![]() - temperature, Ê;
- temperature, Ê; ![]() - Hamiltonian;
- Hamiltonian; ![]() - Cartesian coordinates, m;
- Cartesian coordinates, m; ![]() - intensity of the heat internal
source in
- intensity of the heat internal
source in ![]() , Wt/m3;
, Wt/m3; ![]() - Stephan-Boltsman constant,
Wt/(m2×Ê4); F - diathermic area surface;
- Stephan-Boltsman constant,
Wt/(m2×Ê4); F - diathermic area surface; ![]() - distance between points x and y,
laying on surfaces F, m;
- distance between points x and y,
laying on surfaces F, m; ![]() - surface emissivity F;
- surface emissivity F; ![]() - corners between normals to surface F in points x, y and a vector
- corners between normals to surface F in points x, y and a vector ![]() , rad; qr - radiant flux density, Wt/m2;
, rad; qr - radiant flux density, Wt/m2; ![]() - temperature of crystallization, Ê;
- temperature of crystallization, Ê; ![]() - an interval of smoothing, Ê;
- an interval of smoothing, Ê; ![]() - an external normal to border
- an external normal to border ![]() ;
; ![]() - effective heat-transfer coefficient,
Wt/(m2×Ê);
- effective heat-transfer coefficient,
Wt/(m2×Ê); ![]() – temperature of environment, Ê;
– temperature of environment, Ê; ![]() ,
, ![]() – values of function on the right and
to the left of
– values of function on the right and
to the left of ![]() , Ê;
, Ê; ![]() ;
; ![]() – vector of heat-flux density by
conductivity, Wt/m2;
– vector of heat-flux density by
conductivity, Wt/m2; ![]() – total heat flux density in diathermic medium,
Wt/m2;
– total heat flux density in diathermic medium,
Wt/m2; ![]() – total heat flux density in transparent medium, Wt/m2;
– total heat flux density in transparent medium, Wt/m2;
![]() – total heat flux density in non-transparent
medium (heat conductivity medium), Âò/ì2;
– total heat flux density in non-transparent
medium (heat conductivity medium), Âò/ì2;![]() - solid-melt joint space (area);
- solid-melt joint space (area); ![]() – areas (elements of construction) number;
– areas (elements of construction) number;
![]() .
.
So the system of the
integro-differential equations (1) together with BC (3), (4) is the full mathematical formulation of
assigned problem.
As numerical solution of a heat
equation technique is described enough in [6], we shall restrict our analysis by
consideration of the solution of integrated equation of system (1) technique.
First of all we shall execute some transformations. To do this the system (1) of
integrated equation of radiation heat transfer has to be written in a digital
form on conditions that
on the Gj values of T4, qr are accepted constants
![]() , (5)
, (5)
where H and G – influence factors for temperature and radiant
heat-flux density; N – number of nodes on boundary G; i
– index of a source; j – index of a current node; Gj – element of discretization G;
![]() , (6)
, (6)
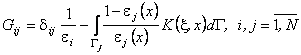 , (7)
, (7)
![]() - Kronecker symbol.
- Kronecker symbol.
Assume
that emissivity does not depend from x, so ![]() on Gj. Such
assumption allows to simplify and to eliminate considerably a number of H and G calculations.
on Gj. Such
assumption allows to simplify and to eliminate considerably a number of H and G calculations.
Then
expression (7) transfers to
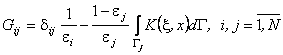 (8)
(8)
To
take into account (8) influence factors equation will be presented
as
![]() , (9)
, (9)
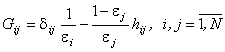 ,
(10)
,
(10)
where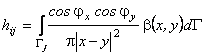 . (11)
. (11)
So a influence factors calculation is reduced to only one integral (11).
Equations (9) and (10) are available for the single nodes at linear elements (or
for constant elements). At double nodes the situation is quite different:
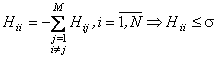 , (12)
, (12)
![]() . (13)
. (13)
Equations (12) and (13) are available
both for double nodes as well as for single nodes. However, at the single or
central nodes is accepted, that
![]() , therefore it is available
, therefore it is available ![]() .
.
The
order of hij calculation
depends on a type of boundary elements obtained as a result of digitization of
a boundary surface. For boundary elements we shall choose triangular linear
elements [6]. Thus numbering of tops of the triangles limiting the node j, is carried out so that the top
conterminous with the node j, had number
Let's enter function
![]() .
.
In
each triangle function changes under the linear law, for example, for F and
qr will be
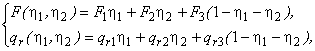 (14)
(14)
coordinates
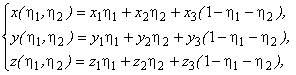
where indexes 1,2,3 – relate to
numbers of tops of triangles; ![]() – oblique coordinates.
– oblique coordinates.
To keep the form of the boundary
equations BEM
(5) together with using of (9), (10), we shall write down hij relate to nodal surface points j. In this case the coefficientò hij even at use of linear elements
becomes independent from function or a stream and can be calculated beforehand.
According to [6] it is obtained
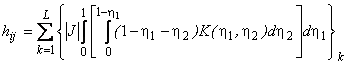 , (15)
, (15)
where L – quantity of
triangles, limiting the node j; k
– index of triangles.
Let's
substitute ![]() from (11) into (15), we'll get
from (11) into (15), we'll get
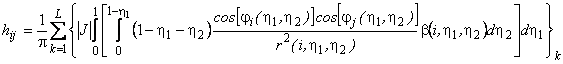 ,(16)
,(16)
where ![]() ;
; ![]() – Jacobian;
– Jacobian;
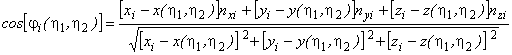 , (17)
, (17)
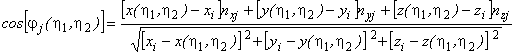 , (18)
, (18)
To take
into account of (17) and (18) for (16) we'll get
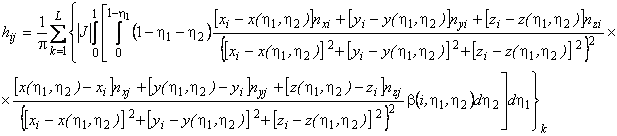
(19)
The integral (19) can be defined
numerically with the using of Hamer’s quadrature [5]
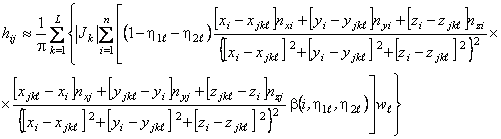 , (20)
, (20)
where ![]() – nodes and weights of quadrature on a simplex;
n – quantity of nodes of quadrature; nx, ny,
nz – directional cosines an external normal to a plane [6];
– nodes and weights of quadrature on a simplex;
n – quantity of nodes of quadrature; nx, ny,
nz – directional cosines an external normal to a plane [6]; ![]() –
coordinates of nodes [6].
–
coordinates of nodes [6].
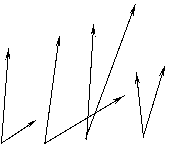
How
to definite ![]() . Let’s in space there is a triangle
with vertexes
. Let’s in space there is a triangle
with vertexes ![]() and a vector
and a vector ![]() with terminuses
with terminuses ![]() and
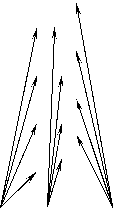
and ![]() (fig. 1).
It is necessary to define conditions at which vector
(fig. 1).
It is necessary to define conditions at which vector ![]() crosses an interior of a triangle
crosses an interior of a triangle ![]() .
.
Assumption
1. Points 1, 2 and 3 don't lie on one straight line.
Conditions of check
![]() or
or ![]() .
.
The assumption 2. Points À and  lay on the different sides from a plane in which the ![]() lays.
lays.
Terms of verification

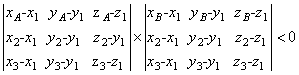 .
.
Fig. 1. The scheme for calculation ![]()
At the given
assumptions vectors ![]() ,
, ![]() è
è
![]() create basis of
space
create basis of
space ![]() . Let's perform a vector
. Let's perform a vector ![]() as linear
combination of vectors
as linear
combination of vectors
![]() ,
, ![]() and
and ![]() :
:
![]() . (21)
. (21)
Than
a vector ![]() crosses an interior of a triangle
crosses an interior of a triangle ![]() if and only if, when
if and only if, when
![]() . (22)
. (22)
Let's labeling ![]() . To calculate
. To calculate ![]() we shall multiply scalar equation (21) on
we shall multiply scalar equation (21) on ![]() . We shall obtain the linear
equations system
. We shall obtain the linear
equations system
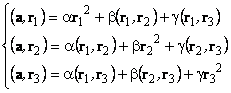 . (23)
. (23)
To reduce a number
of arithmetic operations at the
calculation ![]() solution of the (23) will be performed as follows. The matrix determinant of the system (23) can be obtained by means of
algebraic additions
solution of the (23) will be performed as follows. The matrix determinant of the system (23) can be obtained by means of
algebraic additions ![]()
![]() .
.
Let's
make a matrix of algebraic additions taking into account of symmetry (23)
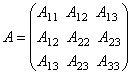
Condition
of (22) will be hold, if all components of a vector
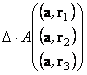
are positive, so
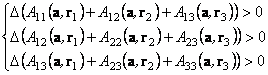 . (24)
. (24)
On finishing of all coefficients of
the ensemble ![]() calculation it is possible to write down system of the nonlinear
algebraic equations according to boundary conditions (3), (4). In the vectorial
form, after performance of partial linearization on temperature by
calculation it is possible to write down system of the nonlinear
algebraic equations according to boundary conditions (3), (4). In the vectorial
form, after performance of partial linearization on temperature by
 (25)
(25)
where ![]() ,
,![]() – belong to heat conductivity;
– belong to heat conductivity; ![]() ,
,![]() – belong to radiating heat exchange;
– belong to radiating heat exchange; 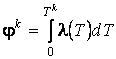 – Kirchhoff's direct
transformation [5,6]; B – a vector, connected with an
internal source of heat.
– Kirchhoff's direct
transformation [5,6]; B – a vector, connected with an
internal source of heat.
The temperature is calculated
in iterative cycle from the solution of (25) according to equation ![]() . First three equations describe the conductive
heat transfer under boundary conditions (3), (4), and two following - to
radiating heat transfer at BC of Dirichle, Neumann as well as contact
conditions. In other words at radiating heat transfer BC of convection type
are not considered. Last equation of system (25) describes conditions of
contact on transparent border for radiation of heat-conductive bodies.
. First three equations describe the conductive
heat transfer under boundary conditions (3), (4), and two following - to
radiating heat transfer at BC of Dirichle, Neumann as well as contact
conditions. In other words at radiating heat transfer BC of convection type
are not considered. Last equation of system (25) describes conditions of
contact on transparent border for radiation of heat-conductive bodies.
The solution of system (25) is performed
by Gauss’s method taking
into account a banded matrix type. Solution of the system (25) takes unknown temperatures
and density of normal streams on borders [6].
Accordingly to the described
method the software of [6], has been modified regarding maintenance of
calculations of radiating heat transfer between complicated shape bodies taking
into consideration surfaces screening. In fact some modifications have been
made to the file of tasks, the module of the linguistic analysis of a
file-task, the module of calculation of influence coefficients and to 2the
module of band matrix on the set boundary conditions.
The modified software was verified by some simple tests for which exact solutions
[7, 8] are known.
Test 1. Radiating heat transfer
between flat surfaces. There are two parallel infinite extent plates with
diathermic environment [7] between them (fig. 2(à)): temperatures (t) and plates surfaces emissivity (e) t1 = 127;500;1200 °Ñ and t2 = 50;250;500 °Ñ, e1 = 0,5;0,8 ³ e2 = 0,5;0,6. It is necessary to find heat-flux density between flat surfaces. At the
numerical solution the task is considered as the cube with adiabatic conditions
on lateral surfaces at e = 0 (table 1).
à) flat surfaces |
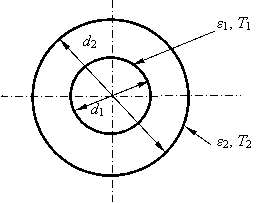
b) cylindrical
surfaces |
Fig. 2. Schemes of radiating heat transfer
Table 1. Analytical and
numerical solutions results comparison at radiating heat transfer between the infinite
extent plates separated by diathermic environment.
|
Temperature of surfaces, t1/ t2, °Ñ |
Surfaces emissivity, e1/e2 |
Heat-flux density, q12, Wt/m2 |
|
|
|
|
The exact decision |
BEM(150
nodes) |
|
127/50 |
0,5/0,5 0,8/0,6 |
278,142 435,352 |
278,142 435,352 |
|
500/250 |
0,5/0,5 0,8/0,6 |
5334,39 8349,47 |
5334,39 8349,47 |
|
1200/500 |
0,5/0,5 0,8/0,6 |
82233,7 128713,6 |
82233,7 128713,6 |
Test 2. Radiating heat transfer
between flat surfaces at presence of screens. A screen emissivity escr = 0,2. Other initial conditions are
the same as in an test 1 (table 2).
Test
3. Radiating heat transfer between cylindrical
surfaces. Diameters of cylinders: d1
=
Test 4. Radiating heat transfer between
cylindrical surfaces at presence of the screen. Diameter and screen emissivity: dscr =
Table 2. Comparison of the analytical
solution with numerical results for radiating heat transfer between infinite
extent plates separated by diathermic environment without
and at the presence of screens
|
Number of screens |
Temperature of surfaces, t1/ t2, °Ñ |
Surfaces emissivity, e1/e2 |
Heat-flux density, q12, Wt/m2 |
|
|
|
|
|
The exact decision |
BEM (150-450 nodes) |
|
0 1 2 |
127/50 |
0,8/0,6 |
435,352 76,436 41,896 |
435,352 76,435 41,895 |
|
0 1 2 |
500/250 |
0,5/0,5 |
5334,39 1333,60 762,055 |
5334,39 1333,59 762,055 |
|
0 1 2 |
1200/500 |
0,8/0,6 |
128713,6 22598,58 12386,67 |
128713,6 22598,56 12386,66 |
Table 3. Comparison of the analytical
solution with numerical results for radiating heat transfer between the
cilindrical surfaces separated with diathermic environment
|
Temperature of surfaces, t1/ t2, °Ñ |
Degree of blackness of surfaces, e1/e2 |
Heat-flux density, q12, Wt/m2 |
|
|
|
|
The exact decision |
BEM (576 nodes) |
|
127/50 |
0,5/0,5 0,8/0,6 |
333,770 527,005 |
335,151 513,848 |
|
500/250 |
0,5/0,5 0,8/0,6 |
6401,26 10107,26 |
6427,75 9854,92 |
|
1200/500 |
0,5/0,5 0,8/0,6 |
98680,45 155811,24 |
99088,79 151921,21 |
Test 5. Stationary heat transfer
through a multilayered wall at boundary conditions of convection type [7,8]: layers number – 3; 1-st
and 3-rd layers heat-conducting, and 2-nd – diathermic environment, thickness
of layers d1 = d2 = d3 =0,12 m; heat conductivity of layers ![]() ; surfaces emissivity 2-nd layer e=0,8;
BC of convection type a1 = 20 Wt/(m2∙Ê), t1 = 1200 °Ñ; a2 = 10 Wt/(m2∙Ê), t2 = 27 °Ñ
(table 5).
; surfaces emissivity 2-nd layer e=0,8;
BC of convection type a1 = 20 Wt/(m2∙Ê), t1 = 1200 °Ñ; a2 = 10 Wt/(m2∙Ê), t2 = 27 °Ñ
(table 5).
Òable 4. Comparison
of analytical solution and numerical results
for radiating heat transfer between the cilindrical surfaces separated by the
diathermic environment without
and at presence of screens
|
Number of screens |
Temperature of surfaces, t1/ t2, °Ñ |
Surfaces emissivity, e1/e2 |
Heat-flux density, q12, Wt/m2 |
|
|
|
|
|
The exact decision |
BEM (576-1152 nodes) |
|
0 1 |
127/50 |
0,8/0,6 |
527,005 110,034 |
513,848 107,480 |
|
0 1 |
500/250 |
0,5/0,5 |
6401,26 1882,73 |
6427,75 1875,30 |
|
0 1 |
1200/500 |
0,8/0,6 |
155811,24 32532,02 |
151921,21 31776,99 |
Table 5. Comparison
analytical solution and numerical results of a stationary problem of complex
heat exchange of a multilayered unlimited flat wall at BC of convection type
|
conductivity Wt/(m∙Ê) |
Temperatures, a multilayered wall, t1/t2/t3/t4, °C |
Heat-flux density, q12, Wt/m2 |
||
|
|
The exact solution |
BEM (1944 nodes) |
The exact solution |
BEM (1944 nodes) |
|
1,5/0,2 |
1129,6/1016,96/1012,6/167,8 |
1129,5/1017,4/1013,0/167,9 |
1408,00 |
1409,246 |
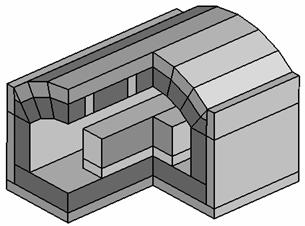
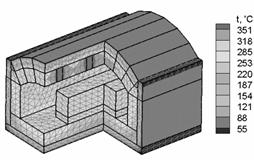
Temperature fields in the tunnel oven
and in the growing joint of the crystallizer were calculated by means of described
software (fig. 3). To achieve the accuracy of
0,001 °Ñ it was necessary to do 5-8 iterations. Results of calculations are performed
on fig. 4. At calculations heat conductivity of solid materials was assumed as
in [9], and emissivity as in [8].
|
1 2 3 4 |
1 2 3 |
|
1 – heat insulator; 2 – fire bricks; 3 – heater; 4 – billets; diathermal medium is placed between
internal surfaces of the oven and external - billets à) tunnel oven |
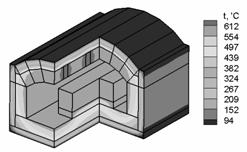
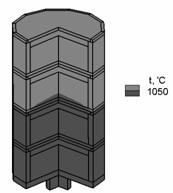
1 – crucible;
2 – crystal or melt; 3 – diathermal medium b) growing joint of a
crystallizer for Bridgman-Stockbarger method |
Fig. 3. Geometrical characteristics of
numerical models of complex heat transfer
|
|
|
|
à) Temperature fields of the tunnel oven at different modes of billets heating
|
|
|
b) |
c) |
|
temperature fields of the crystallizer growth
zone (b), the location and the form of front of crystallization (c) |
|
Fig. 4. Results of calculations of
temperature fields in conditions of complex heat transfer
Conclusions
A new numerical technique is developed
to solve 3D steady-state radiating and radiation-conductive heat transfer
problems in conductive and diathermic medium at borders diffusive reflection with
accounting of screening effect by direct method of boundary elements.
Research supported by the INTAS Project 05-1000008-8111.
Literature:
1.
R.Siegel, J.Howell Thermal Radiation Heat Transfer. – McGraw-Hill Book
Company,
2.
Yuferev V.S., Vasil’ev Ì.G., Proekt L.B. Novyy metod resheniya zadach perenosa izlucheniem v
izluchauzhikh, poglozhauzhikh i rasseivauzhikh sredakh// Jurnal tekhnicheskoy phiziki. – 1997. - Ò. 67, N 9. – P.1-7.
3.
S.Kochuguev, D.Ofengeim, A.Zhmakin
Axisymmetrical radiative heat transfer simulation by Ray Tracing Method,
Proceedings of the 3rd European Conference on Numerical Mathematics and
Advanced Applications, P.
Neittaanmäki, T. Tiihonen and P. Tarvainen (eds.), World Scientific,
Singapore, 2000, pp. 579-586.
4. Boundary Element Methods in Heat Transfer/ Ed: L.C. Wrobel, C.A.Brebbia -
5. C.A.Brebbia, J.C.F.Telles,
L.C.Wrobel
Boundary element techniquus. –
6. Karvatsky A.Ya., Dudnikov P.I., Leleka S.V., A.I.Juchenko An application of boundary element method to simulate 3D thermal conductive problems //Naukovi visty NTUU “KPI”. –2005.-N5.-P.5-13.
7.
Isachenko V.P., Osipova V.À., Sukomel À.S. Teploperedacha /Ucebn. dlya vuzov. - Ì: Energoizdat, 1981. – 416p.
8.
Krasnoshokov Å.À., Sukomel À.S. Zadachnic po teploperedache /Zad. dlya vuzov. - Ì:Energiya, 1969. – 264p.
9. Phizicheskie velichiny. Spravochnik/ Pod red. I.S. Grigop’eva.- Ì.: Energoatomizdat, 1991. -1232p.