Марзан С.А.

Брестский государственный университет имени А.С. Пушкина

 

Задача Коши для линейного дифференциального уравнения с дробной производной Капуто комплексного порядка

 

Обозначим через  модифицированную дробную производную, определяемую формулой

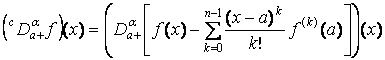                       ,                   (1)

где  – дробная производная Римана-Лиувилля [1] функции , заданной на [a;b], комплексного порядка a (aÎС), Re(a)>0, n=[Re(a)]+1 при aÏN={1,2,…}, и n = a при a Î N. Если a > 0,  (nÎN) и y(x)ÎCn[a;b] – функция, n раз непрерывно дифференцируемая на [a;b], то при aÎN производная  совпадает с обычной производной:

,

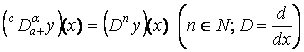а при n – 1 < a < n оператор  представляется в виде композиции оператора дробного интегрирования  [1] и оператора дифференцирования :

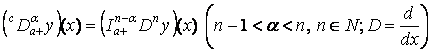                   .               (2)

Конструкция (1) была введена итальянским механиком Капуто [2] в связи с задачами вискоэластичности (см. [2]-[4]), и поэтому выражения (1) и (2) называют дробными производными Капуто порядка aÎС; см. [5], [6], [7, § 2.4.1].

В приложениях часто возникает необходимость в исследовании задачи Коши для линейного дифференциального уравнения с дробной производной Капуто комплексного порядка

                 .             (3)

Обозначим через  класс функций g(x), заданных на [a;b] и таких, что :

               .

Тогда через  (aÎС, Re(a)>0, n=[Re(a)]+1 при aÏN={1,2,…}, и n=a при aÎN) обозначим класс функций y(x), и таких, что ,  :

       ,  .

Справедлива следующая теорема.

Теорема. Пусть , ,  и .

Задача Коши (3) имеет в  единственное решение, определяемое формулой

                            

                             ,

где 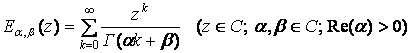 – специальная функция Миттаг-Леффлера.

В частности, единственное решение задачи

                     

дается формулой

                              .

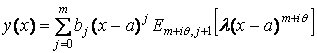Доказательство

Согласно [8] решение задачи (3) равносильно решению интегрального уравнения

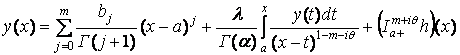                ,            (4)

где  – оператор дробного интегрирования Римана-Лиувилля порядка .

Используем для решения уравнения (4) метод последовательных приближений. Пусть

                                         ,

              ,

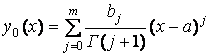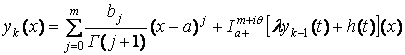Отсюда при  находим

     

        ,

      

   

          ,

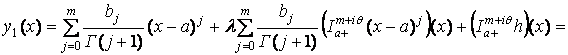
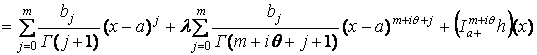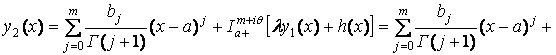
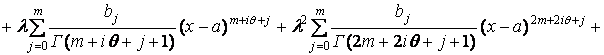
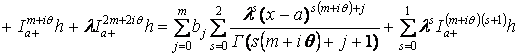что в общем случае приводит к формуле

              ,

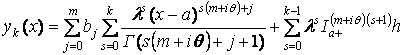Переходя к пределу при , получаем следующее представление искомого решения:

                            

                             .                         (5)

Формула (5) дает единственное решение интегрального уравнения (4), так как соответствующее (4) однородное уравнение

                                      

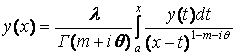
имеет только тривиальное решение ; см. [1, § 2.4, c. 46].

Теорема доказана.

Следствие. При  и  задача Коши

                  

имеет в  единственное решение

                      

                                 

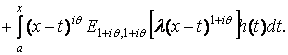
В частности, решение задачи

              

имеет вид

                       .

Непосредственно проверяется, что функции

                      

являются линейно независимыми решениями однородного дифференциального уравнения дробного порядка

                                 

с дробной производной Капуто комплексного порядка .

Этот факт показывает существенное различие между дифференциальными уравнениями натурального и комплексного порядков. Именно, однородное линейное дифференциальное уравнение порядка  с постоянными коэффициентами имеет m линейно независимых решений, в то время как линейное однородное дифференциальное уравнение комплексного порядка   с постоянными коэффициентами может иметь (m+1) линейно независимое решение.

Литература.

1. Самко С.Г., Килбас А.А., Маричев О.И. Интегралы и производные дробного порядка и некоторые их приложения. – Минск: Наука и техника, 1987. – 687 с.

2. Caputo M. Linear model of dissipation whose Q is almost frequency independent // Geophis. J. Astronom. Soc. – 1967. – Vol. 13. – P. 529-539.

3. Caputo M. Elasticita e Dissipation. Bologna: Zanichelli, 1969.

4. Caputo M., Mainardi F. Linear models of dissipation in an elastic solids // Riv. Nuovo Cimento. – 1971. – Vol. 1. – P. 161-196.

5. Mainardi F. Fractional calculus: some basic problems in continuum and statistical mechanics. Fractals and Fractional Calculus in Continuum Mechanics // Viena: Springer. – 1997. – P. 291-348.

6. Gorenflo R., Mainardi F. Fractional calculus: integral and differential equation of fractional order. Fractals and Fractional Calculus in Continuum Mechanics // Viena: Springer. – 1997. – P. 223-276.

7. Podlulny I. Fractional differential equations. Mathematics in Sciences and Engineering. – San Diego, 1999. – 198 p.

8. Килбас А.А., Марзан С.А. Нелинейные дифференциальные уравнения с дробной производной Капуто в пространстве непрерывно-дифференцируемых функций // Доклады академии наук. – 2004. – Т. 399, № 1. – С. 7-11.